Progressões Gemétricas e Progressão Aritmética: PA & PG

Hoje você vai aprender um novo tipo de sequência matemática muito frequente nas provas do Enem e dos vestibulares: veja o que são as progressões geométricas. Ou, simplesmente PG. Se esse assunto estiver presente na prova de Matemática Enem, com essa aula você terá alta probabilidade de acertar mais uma questão! Vamos lá?

Você lembra do conteúdo sobre Progressão Aritmética, a famosa PA? E sobre as Progressões Geométricas, as famosas PG? Então, para relembrar em um minuto: a Progressão Aritmética é uma sequência de números bem definida e ordenada, em que cada termo é igual ao anterior somado à razão r.

Veja exemplos  de PA para  relembrar:

• Exemplo 01 – Considere a PA (1, 5, 9, 13, 17, …).  Para chegar à razão, veja que  5-1 = 9-5 = 13-9 = 17-13 = 4. Ou seja, r é igual a quatro.
• Exemplo 02 – Considere a PA (20, 18, 16, 14, …)  Para descobrir a razão ‘r’, pereceba que aqui também há diferença constante entre qualquer termo e seu antecedente. Veja: 18-20 = 16-18 = 14-16 = -2. Ou seja, ‘r’ = -2
• Exemplo 03 – Considere a PA  (5, 5, 5, 5, …).
• Ficou fácil neste caso, certo?
• Está claro que ‘r’ é igual a zero: r = 0  
• PA & PG são temas que sempre caem. Se liga nos resumos desta aula.   

Diferenças entre PA e PG

O que muda entre a PA e a PG  é justamente a definição, pois apesar de progressão aritmética e geométrica serem tipos de sequências, elas têm suas diferenças e por conta disso, têm propriedades diferentes também.

Progressão geométrica (PG) é uma sequência bem definida e ordenada onde cada termo é igual ao anterior multiplicado pela razão q.

Podemos perceber isso pela fórmula: an+1=an.q. Onde n pertence aos números naturais sem o 0 (N*={1,2,3,…}), an+1 é o termo da posição n+1, an é o termo da posição n e q é a razão da progressão geométrica.

Resumo de Progressão Arimética – PA

Confira com o professorar Lucas o básico de PA. Ele é do canal do Curso Enem Gratuito . Depois tem a aula sobre as Progressões Geométricas também. Uma de cada vez. Bora lá!

Viu como dá sim para aprender e se garantir? Confira agora um exemplo bem prático:

Veja neste exemplo bem simples do site www.da-educa.com a diferença entre uma ‘PA de 4’ e uma ‘PG de 4’:  

Veja as Progressões Geométricas:

Para entendermos melhor essa definição de Progressão Geométrica na Matemática Enem, vou dar alguns exemplos. Olhe atentamente para essa sequência: (4, 8, 16, 32, …). Reparou que essa sequência é infinita?

Pois é, além de ser uma sequência infinita, essa sequência é uma progressão geométrica que tem primeiro termo a1=4 e razão q=2.

Solução: Caso você não tenha entendido o motivo da razão q ser 2, basta dividir qualquer termo (menos o primeiro) pelo seu antecessor: 8 dividido por 4 é igual a 2 (pois 4×2=8), 16 dividido por 8 é igual a 2 (pois 8×2=16), e assim por diante. Viu como é fácil encontrar a razão de uma progressão geométrica?

Resumo sobre PG para fixar o conteúdo:

Agora veja com o professor Lucas as dicas sobre como identificar e como resolver as Progressões Geométricas.

Outro exemplo de PG:

Agora olhe para a seguinte PG: (1, -2, 4, -8, 16,…). Você consegue me dizer qual é o primeiro termo a1 e a razão q dessa PG?  Acertou quem disse que a1=1 e q=-2. Para encontrar o primeiro termo basta ver qual termo ocupa a posição 1 da sequência (1,-2,4,-8,16,…) e podemos ver, tranquilamente, que o número 1 ocupa a posição 1 da sequência.

Solução da Progressão Geométrica:

Para encontrar a razão da PG basta dividir qualquer termo (menos o primeiro) pelo seu antecessor. Repare aqui que não há necessidade de fazermos várias divisões para verificar se a razão é a mesma (porque deve ser a mesma se for uma PG).

Isso porque eu já afirmei quando informei pela primeira vez a sequência (1,-2,4,-8,16,…) que ela é uma PG. Perceba a importância disso: sempre que alguma sequência for dita sendo PA ou PG, ela possui uma razão que é constante!

 

Veja mais um tipo curioso de sequência. Repare a PG (7, 7, 7, 7, …). Acertou quem disse que a razão é q=1. Repare que essa PG também é uma PA de razão r=0. Curioso não?! São clássicos das Progressões Geométricas.

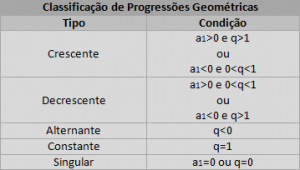
Antes de passar a fórmula do termo geral da PG , veja como classificamos as PGs. Pois, assim como PAs têm classificações, PGs também têm! Para mostrá-los as classificações, nessa aula de Matemática Enem, há uma tabela contendo o nome e a condição necessária para uma PG pertencer àquele tipo.

Classificação das Progressões Geométricas

Para resolver os exercícios envolvendo progressões geométricas é de fundamental importância conhecer a Fórmula do Termo Geral de uma PG.

Na imagem abaixo, você verá como podemos encontrar essa fórmula (considere a1 sendo o primeiro termo e q a razão):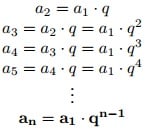

Propriedades da Progressão Geométrica:

Como foi falado anteriormente, a progressão geométrica possui propriedades diferentes da progressão aritmética.

1) A primeira propriedade é que para três termos consecutivos de uma PG, o quadrado do termo médio é igual ao produto dos outros dois:

2) A segunda propriedade é que numa PG com n termos, o produto de dois termos equidistantes dos extremos é igual ao produto destes extremos. Por exemplo: digamos que numa PG de n termos, ap e ak são dois termos equidistantes dos extremos. Pela segunda propriedade, temos: .

Lembre-se, essas propriedades são muito importantes e, quem sabe, pode ajudar você em resoluções de questões de Matemática Enem.

Para finalizar nossa aula de Matemática Enem, vamos verificar como somamos termos de uma PG. Primeiramente, é importante sabermos que podemos ter PGs convergentes e divergentes.

Uma PG é dita convergente quando -1<q<1 e é dita divergente quando não é convergente. A fórmula da soma dos n primeiros termos de uma PG (convergente ou divergente) é a seguinte: Nas PGs convergentes com infinitos termos, conforme vamos somando os termos, percebemos que o valor das somas tende a um valor limite. Faça um teste com a PG convergente  e você perceberá que a soma tenderá ao valor 8. Porém, para as PGs convergentes com infinitimos termos, temos a seguinte fórmula que pode ser usada para calcular a soma de todos os termos: .

Aula Gratuita

Tenho certeza que você está curioso para saber como aplicar a fórmula do termo geral da PG e assim aprofundar ainda mais seus conhecimentos para a Matemática Enem. Para isso, disponibilizo abaixo o vídeo de uma aula sobre progressão geométrica do professor Nivaldo Galvão:

Essa foi a aula de hoje de Matemática Enem. Espero que tenha gostado e desejo-lhe excelentes estudos!

A aula foi elaborada pelo professor Mauricio Policarpo, que fez  graduação de Matemática da UFSC e  foi bolsista da Olimpíada Regional de Matemática de Santa Catarina

Revisão completa de Matemática no Curso Enem Gratuito

Você já sabe: Matemática é uma prova completa no Enem, com 45 questões, e que vale até 200 pontos na sua nota geral. Acertar as questões de Matemática faz toda a diferença para você se dar bem depois nas Notas de Corte do Sisu, do Prouni, e do Fies. Aumente suas chances com as aulas do Curso Enem Gratuito.

 O Curso Enem Gratuito tem aulas Online disponíveis 24 horas, com todas as matérias das provas objetivas e também as dicas de Redação Enem Nota 1000. Veja o Curso Pré-Enem e também faça os testes do Simulado Enem Online Gratuito, com todas as matérias.

EXERCÍCIOS DE MATEMÁTICA ENEM

01. (UFSC) Numa PG de 6 termos a razão é 5. O produto do 1° termo com o último é 12500. Determine o valor do 3° termo. Observação: Considere a PG de termos positivos.