Matemática Enem: Revise os tipos de funções!
Nesta aula, serão definidos os seguintes temas: função composta e função inversa. Serão abordados os meios para a obtenção de cada uma assim como suas definições.
Faça parte desta aula e se garanta para Matemática no Enem!
Função Composta
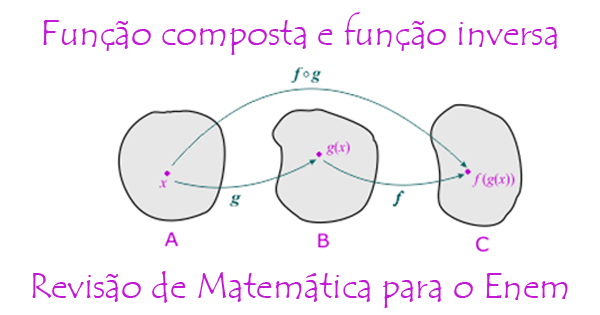
Devemos entender que a função composta nada mais é que uma função “dentro” de outra. Usam-se duas notações para se representar uma composição de funções, ou seja: (1) F(g(x)) (2) Fog.
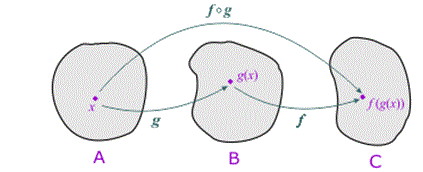

Cálculo de uma função composta
Para podermos calcular essa composição, devemos começar representando as funções de fora para dentro, ou seja, primeiro a função f(x) e logo em seguida a função g(x), “dentro” da primeira função. Quando por exemplo, calculamos f(1) na função f(x) = x + 2, basta substituirmos todas variáveis x pelo valor 1, então teríamos, pelo exemplo f(1) = 1 +2, então f(1) = 3. No caso da função composta é a mesma coisa, a mudança é apenas que ao invés de substituirmos o “x” por algum número, substituímos o “x” por uma função correspondente.

Função Inversa
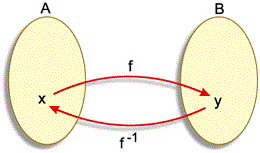
Devemos entender que a função inversa “transforma” o que é domínio em imagem e “transforma” o que é imagem em domínio. Antes de fazermos essa transformação, devemos tomar cuidado para ver se a função é bijetora( injetora e sobrejetora ao mesmo tempo), pois se não for, não existirá função inversa.
Siga então os passos listados para encontrar a função inversa de dada função: (1) Verifique se a função dada é bijetora (2) Em caso afirmativo, substitua, onde existir “x” na função troque por “y” e vice-versa. (3) Isole o “y” Esses são os passos para se encontrar a função inversa.
A notação para a função inversa é dada a seguir: Função inversa= f-1 Ou seja, a notação da inversa é a função “elevada” a menos 1. Devemos lembrar que a notação f(x) é a mesma coisa que y.
Definição: Dada a função ƒ: A em B, chama-se função inversa de ƒ, indicada por ƒ -1(x), a função ƒ -1 : B em A que associa cada y de B ao elemento x de A, tal que y = ƒ(x).
OBS.:
1) Apenas as funções bijetoras admitem função inversa.
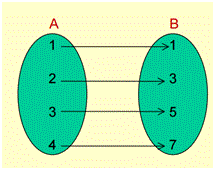
Nota sobre Função Bijetora
Uma função ƒ: A em B é bijetora quando ƒ é sobrejetora e injetora.
Exemplo:
2) Regra Prática para obtenção de uma Função Inversa:
- Trocar ƒ(x) ou a função que está representada por y.
- Trocar x por y e y por x.
- Isolar y para representá-lo como função de x.
- Trocar y por ƒ -1 (x).
Exemplo:
1) Obter a função inversa da função ƒ(x) = 3x – 2.
ƒ(x) = 3x – 2
y = 3x – 2
x = 3y – 2
3y = x + 2
y = (x + 2)/3
ƒ -1 (x) = (x + 2)/3
Assista às aulas abaixo que irão complementar os seus estudos!