Proporção, Regra de Três Simples e Composta – Revisão Encceja

No post de hoje você vai saber tudo sobre Proporcionalidade e descobrir que na verdade já usava na vida prática – como em cálculo de pagamento por hora de trabalho ou no tempo que você leva para fazer uma viagem dependendo da velocidade.

Vamos ver também como usar a Regra de Três Simples, assim como a Regra de Três Composta. Para isso vamos usar um exemplo onde você vai fazer cálculos simples para descobrir quantas pessoas precisam ser contratadas para fazer um determinado serviço, dependendo da quantidade de dias necessários e também variando quantas horas são trabalhadas por dia.

Vem com a gente revisar proporcionalidade para você arrasar na prova do Enem! A proporção na matemática significa uma igualdade entre duas razões. Por exemplo, podemos dizer que 1:2 = 3:6 (lê-se: “1 está para 2 assim como 3 está para 6”). Também podemos escrever na forma de fração:

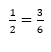É simples assim!

Dica do professor: Para entender o conceito de proporcionalidade você precisa saber antes o que é razão na matemática: A razão na matemática significa uma relação entre dois valores.

Na hora de planejar e organizar os estudos você pode usar uma razão para se preparar: você pode calcular o número de horas que você deve estudar individualmente em relação ao número de horas que assiste aulas (ou videoaulas).

Uma sugestão é que para cada hora de videoaula se estude duas horas individualmente, em outras palavras a razão das suas horas de estudo é de 1:2 (lê-se “um para dois”).  Veja este post onde explico de maneira simples o que é razão.

E a Regra de Três?

A famosa Regra de Três é a maneira prática de usar a proporcionalidade para descobrir um valor que não sabemos.

• Temos dois tipos de proporcionalidade:
• Grandezas diretamente proporcionais; e,
• Grandezas inversamente proporcionais.

Um exemplo de uso da regra de três para grandezas diretamente proporcionais é calcular o pagamento de uma semana de trabalho onde você recebe por horas trabalhadas.

Se você recebe R$ 100,00 Reais por hora trabalhada e você trabalhou 20 horas na semana, quanto será o total recebido nessa semana? Vamos resolver usando a regra de três:

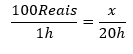
O x é o valor que queremos descobrir, nesse caso, o total recebido nessa semana. Reorganizando temos:

Ou seja,  x = 2000 Reais

E, quando temos uma Grandeza diretamente proporcional, significa que quanto mais horas forem trabalhadas maior será o pagamento. Assim como se diminuir a quantidade de horas também vai diminuir o valor do pagamento. As duas grandezas estão aumentando ou diminuindo na mesma proporção.

Veja agora uma aula sobre Regra de Três, com exemplos e exercícios resolvidos, para você fixar bem o que está aprendendo. É com o professor Sarkis, do nosso canal Curso Enem Gratuito. Em seguida continue no post, para aprender as Grandezas inversamente proporcionais.

E as grandezas inversamente proporcionais? Onde aparecem?

O exemplo clássico é a velocidade média. Imagine que vou viajar a distância de 300Km. Se eu for bem devagar, por exemplo, na velocidade média de 50Km/h, vou demorar 6h para terminar a viagem. Mas se eu for a 100Km/h, vou demorar 3h para completar a viagem.

Observe que quando a velocidade dobra (aumenta) o tempo cai para a metade (diminui).
Vamos usar uma regra de três para descobrir quanto tempo vou levar se minha velocidade média for 60Km/h:

reorganizando:

e assim,

Observe atentamente que a velocidade é inversamente proporcional ao tempo gasto, mas na hora de calcular usando a regra de três, o truque foi usar a proporção direta entre distância e tempo, já que o tempo vai aumentar se a distancia aumentar.

E aproveitamos também que a velocidade média dada em Km/hora é a razão entre a distância percorrida no tempo de 1h.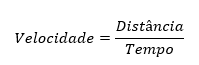

Então, se aparecer uma questão de proporcionalidade na sua frente, a primeira coisa a fazer é descobrir se a proporção é direta ou inversa. Se conhecemos 3 valores e queremos descobrir o quarto valor é uma regra de três Simples como os exemplos acima.

O problema pode ficar mais interessante se temos mais de uma proporção no mesmo problema, nesse caso vamos tem uma regra de três Composta. E agora? O que fazer?

Para a Regra de Três Composta, a gente precisa organizar direitinho as informações do problema em colunas com o x da questão (o valor que você quer descobrir) na primeira coluna. É muito importante colocar o mesmo tipo de valor em cada coluna e ver se está na mesma unidade de medida também. Depois disso, vamos analisar cada proporção se é direta ou inversa.

Veja um exemplo de organização em colunas que apareceu na prova do Enem:

(ENEM – 2009) Uma escola lançou uma campanha para seus alunos arrecadarem, durante 30 dias, alimentos não perecíveis para doar a uma comunidade carente da região. Vinte alunos aceitaram a tarefa e nos primeiros 10 dias trabalharam 3 horas diárias, arrecadando 12 kg de alimentos por dia. Animados com os resultados, 30 novos alunos somaram-se ao grupo, e passaram a trabalhar 4 horas por dia nos dias seguintes até o término da campanha.

Admitindo-se que o ritmo de coleta tenha se mantido constante, a quantidade de alimentos arrecadados ao final do prazo estipulado seria de: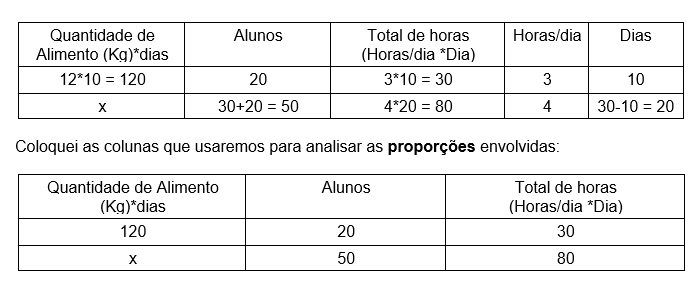

Olhe apenas a primeira e a segunda coluna e se pergunte: Se a quantidade dos alimentos arrecadados está aumentando, a quantidade de alunos deve ser maior ou menor? Será maior.

Então a primeira e a segunda razão são diretamente proporcionais pois ambas estão aumentando nessa proporção.

Agora olhe apenas a primeira e a terceira: Se a quantidade dos alimentos está aumentando, a quantidade de horas trabalhadas foi maior ou menor? Maior.

Então a primeira e a terceira razão são também diretamente proporcionais.

Ufa! Essa foi a parte mais difícil!

E temos que multiplicar os valores das colunas que não têm x e fazer a regra de três simples, com a coluna do x e a coluna das multiplicações, veja:

Agora é só calcular a regra de três (também conhecida como “multiplicar cruzado”) e correr para o abraço!

x*600 = 120*4000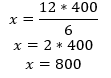

Mas, veja que o problema queria saber qual a quantidade de alimentos arrecadados ao final do prazo estipulado e o nosso x era apenas a quantidade de alimentos arrecadados nos últimos 20 dias. A resposta do problema era 920Kg pois 920 = 120 + 800 é a soma dos alimentos arrecadados nos primeiros 10 dias (120) com alimentos arrecadados nos outros 20 dias (800).

A última coisinha que preciso contar pra vocês é que no caso de alguma das proporções ser inversamente proporcional em um problema com mais de uma proporção, o que deve ser feito é inverter os valores da coluna que não for diretamente proporcional com a coluna do x antes de multiplicar.

Por exemplo:

Para construir uma biblioteca, 30 pessoas trababalharam 6 horas por dia e construiram a biblioteca em 4 dias.

Quantos dias seria preciso para 12 pessoas construirem a mesma biblioteca trabalhando 10 horas por dia?

Montando as colunas temos:

Note que se aumentarmos as pessoas trabalhando vamos precisar de menos dias, ou seja, a primeira e a segunda coluna são inversamente proporcionais.

E se aumentarmos o número de horas trabalhadas no dia precisaremos de menos dias também, assim, a primeira e a terceira colunas também são inversamente proporcionais.

Como a segunda e a terceira coluna são as duas inversamente proporcionais a primeira, podemos multiplicá-las:

E ficamos com uma regra de três simples mas com proporções inversas.

Então, a nossa solução vai ser resolver a proporção “desinvertida”:

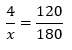
E “multiplicando cruzado”:

x*120=4*180

Ou seja:

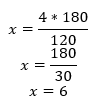
Exercícios

1. (ENEM-2016) Até novembro de 2011, não havia uma lei específica que punisse fraude em concursos públicos. Isso dificultava o enquadramento dos fraudadores em algum artigo específico do Código Penal, fazendo com que eles escapassem da Justiça mais facilmente. Entretanto, com o sancionamento da Lei 12.550/11, é considerado crime utilizar ou divulgar indevidamente o conteúdo sigiloso de concurso público, com pena de reclusão de 12 a 48 meses (1 a 4 anos). Caso esse crime seja cometido por um funcionário público, a pena sofrerá um aumento de 1/3.

Disponível em: www.planalto.gov.br. Acesso em: 15 ago. 2012

Se um funcionário público for condenado por fraudar um concurso público, sua pena de reclusão poderá variar de

(a) 4 a 16 meses.
(b) 16 a 52 meses.
(c) 16 a 64 meses.
(d) 24 a 60 meses.
(e) 28 a 64 meses.

2. (ENEM-2016) Uma empresa europeia construiu um avião solar, como na figura, objetivando dar uma volta ao mundo utilizando somente energia solar. O avião solar tem comprimento AB igual a 20m e uma envergadura de asas CD igual a 60m.

Para uma feira de ciências, uma equipe de alunos fez uma maquete desse avião. A escala utilizada pelos alunos foi de 3 : 400.

A envergadura CD na referida maquete, em centímetro, é igual a

(a) 5.
(b) 20.
(c) 45.
(d) 55.
(e) 80.

3. (ENEM-2016) Um clube tem um campo de futebol com área total de 8000m², correspondente ao gramado. Usualmente, a poda da grama desse campo é feita por duas máquinas do clube próprias para o serviço. Trabalhando no mesmo ritmo, as duas máquinas podam juntas 200m² por hora. Por motivo de urgência na realização de uma partida de futebol, o administrador do campo precisará solicitar ao clube vizinho máquinas iguais às suas para fazer o serviço de poda em um tempo máximo de 5h.

Utilizando as duas máquinas que o clube já possui, qual o número mínimo de máquinas que o administrador do campo deverá solicitar ao clube vizinho?

(a) 4
(b) 6
(c) 8
(d) 14
(e) 16

Respostas:

1 (c) 16 a 64 meses.
2 (c) 45
3 (d) 14