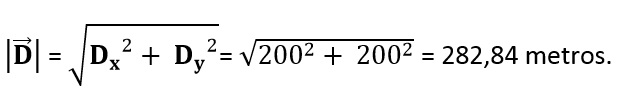Tá difícil mandar bem nos exercícios de Soma de Vetores? Então, vamos descomplicar aqui, porque sempre caem nas provas questões sobre Vetores. Veja um resumo completo sobre a Soma Vetorial. Confira abaixo a teoria, uma aula com resolução de exercícios, e um simulado no final.
Você lembra como fazer o cálculo da Soma Vetorial? Revisão gratuita aqui. Confira nesta aula preparatória de Física Enem, será apresentado o vetor e como se deve proceder para realizar uma soma vetorial. Em seguida serão diferenciadas grandezas vetoriais e grandezas escalares, com conceituação e exemplo.
Para iniciar esta aula sobre grandezas vetoriais e escalares, devemos definir o que é um vetor, e como realizar operações com este. A partir disto poderemos definir grandezas vetoriais e escalares, conceitos que podem ser cobrados na prova do Enem.
O vetor pode ser definido com uma seta ou flecha, que num referencial apropriado, seu comprimento representa o módulo do vetor (dimensão), a direção da flecha indica a direção do vetor e a posição da ponta da flecha indica o sentido da flecha. No desenho abaixo, está um vetor (em vermelho) num referencial de eixos X e Y. O módulo (comprimento do vetor) é igual a 4 cm. Sua direção é definida pelo ângulo de 45° com o eixo X. E o sentido é para onde ela aponta, neste caso nordeste (NE).
No desenho abaixo, está um vetor (em vermelho) num referencial de eixos X e Y. O módulo (comprimento do vetor) é igual a 4 cm. Sua direção é definida pelo ângulo de 45° com o eixo X. E o sentido é para onde ela aponta, neste caso nordeste (NE).
Um vetor é nomeado por uma letra acompanhada com uma seta sobre ela: A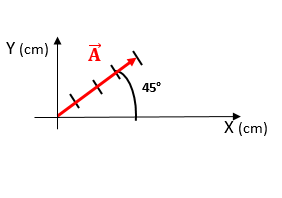 Vetores estão na mesma direção se estiverem paralelos entre si.
Vetores estão na mesma direção se estiverem paralelos entre si.
Vetores tem a mesmo sentido se tiverem as flechas apontando para um mesmo lugar.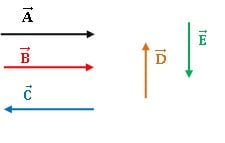
A, B e C estão na mesma direção.
A e B estão no mesmo sentido.
A e B tem sentido oposto ao vetor C.
D e E estão na mesma direção.
D e E tem sentidos opostos.
O sentido de um vetor pode ser definido a partir da rosa dos ventos (desenho abaixo, que mostra os quatro Pontos Cardeais: Norte; Sul; Leste; e Oeste). Com este referencial podemos dizer: A e B estão apontando no sentido leste.
A e B estão apontando no sentido leste.
C aponta no sentido oeste.
D aponta no sentido norte.
E aponta no sentido sul.
VETORES são usados para:
Indicar a posição de um objeto – O carro esta no km 50, na direção e sentido Leste. Sua posição é representada pelo vetor A: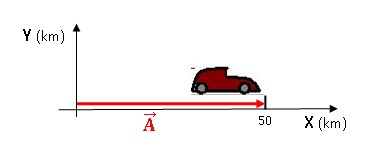
Indicar uma força: O bloco é empurrado com uma força F de modula 5 Newton e na direção e sentido positivo do eixo X.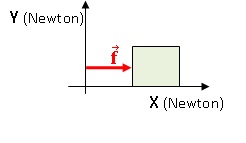
Aula gratuita sobre como fazer a soma de vetores:
Veja com o professor Márcio Rosseto, do canal Curso Enem Gratuito, uma aula show sobre como fazer a soma de vetores pelo método do Paralelogramo e Poligonal. É para você gabaritar nas provas. Confira:
Gostou da aula com o professor Márcio Rosseto? Veja agora outra explicação, para você aprender de vez:
Adição vetorial gráfica: Com este método a soma de vetores é realizada desenhando os vetores, do qual se quer saber a soma, em uma sequência.
Exemplo: Queremos saber a soma dos vetores S = G + F, onde S é o vetor resultante dessa soma.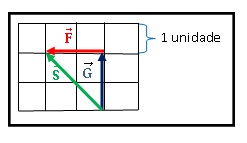 Desenhamos o vetor G, depois desenhamos o vetor F na extremidade (ponta) do vetor G.
Desenhamos o vetor G, depois desenhamos o vetor F na extremidade (ponta) do vetor G.
O vetor resultante é um vetor que começa no inicio do vetor G e termina na ponta do vetor F.
O mesmo pode ser feito para encontrar o vetor resultante S da soma do vetor S = H + G.
Se a extremidade do último vetor da soma, coincidir com a origem do primeiro vetor, isso significa que o vetor resultante é nulo.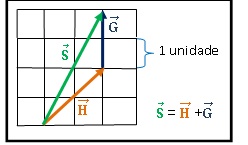
Aula Gratuita sobre Decomposição de Vetores
Confira outra aula com o professor Rosseto, do canal Curso Enem Gratuito, mostrando agora para você como fazer a Decomposição de Vetores:
Gostou da nova aula? Veja abaixo outra explicação sobre a Decomposição de Vetores:
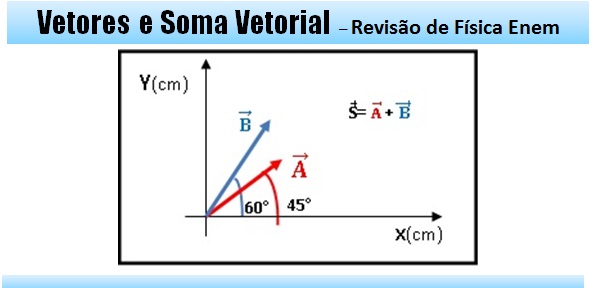
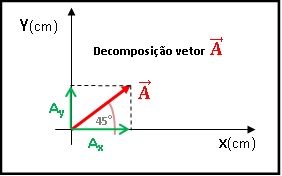
Adição vetorial por decomposição: Sabendo que o vetor A tem módulo iguala 4 cm, e o vetor B tem módulo igual a 5 cm, vamos calcular a soma desses vetores S = A + B.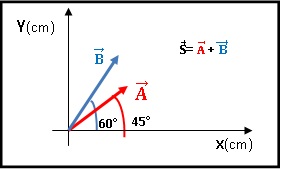 Primeiro devemos decompor os vetores, vamos começar com o vetor A, em suas componentes x e y (ver figura). Onde |A| representa o módulo.
Primeiro devemos decompor os vetores, vamos começar com o vetor A, em suas componentes x e y (ver figura). Onde |A| representa o módulo.
Ax= |A|cos 45° = (4).cos 45° = (4).0,70 = 2,82
Ay= |A|sen 45° = (4).sen 45° = (4).0,70 = 2,82
Fazendo o mesmo com o vetor B:
Bx= |B|cos 60° = (5).cos 60° = (5).0,50 = 2,50
By= |B|sen 60° = (5).sen 60° = (5).0,86 = 4,33
 Assim o vetor resultante S terá componentes iguais:
Assim o vetor resultante S terá componentes iguais:
Sx= Ax+Bx = 2,82 + 2,50 = 5,32
Sy= Ay+By = 2,82 + 4,33 = 7,15
Para encontrar o módulo do vetor resultante basta realizar o seguinte calculo:
|S| = √Sx^2+ Sy^2= √5,32^2+ 7,15^2 = 8,91 cm
E o ângulo que o vetor resultante forma com o eixo X é dado por:
Tan (ângulo) = Sy/Sx = 7,15/5,32, realizando o cálculo teremos ângulo =53,39°
Agora podemos desenhar o vetor resultante no gráfico, assim observar sua posição no gráfico.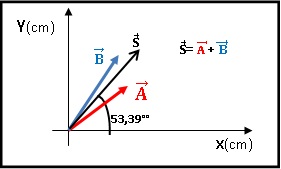
No link abaixo você encontra um simulador que trata da decomposição de vetores, este pode te ajudar a compreender o posicionamento dos componentes de um vetor, num plano X e y.
http://objetoseducacionais2.mec.gov.br/bitstream/handle/mec/10640/decompvetores.swf?sequence=1
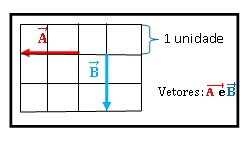
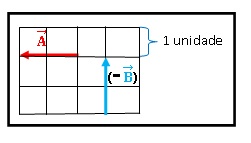
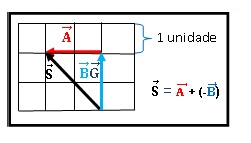
Além de serem somados dois vetores, também podemos subtraí-los, para tal basta inverter o sentido (trocar a ponta) de um dos vetores, e então prosseguir como se estivesse resolvendo um soma. Como mostra a sequência de figuras abaixo:
S= A – B virar uma soma S = A+ (-B) usando o vetor B no sentido oposto.
Veja agora o Simulado Gratuito:
Vetores – Simulado
.
Você pode aprender mais sobre vetor e suas definições, com uma simulação apresentada no link. Assim fica mais fácil estudar Física Enem para sua prova deste ano!
Dic a 02: Você pode acessar o link abaixo e trabalhar com um simulador para aprender melhor sobre este método de soma de vetores e se sair bem na prova de Física Enem neste ano.
http://objetoseducacionais2.mec.gov.br/bitstream/handle/mec/10730/somavetorial1.swf?sequence=1
Dica 02: Enem e a Física: Fundamentos de Termologia https://blogdoenem.com.br/enem-2013-fisica-fundamentos-termologia/
Dica 3: Enem – Dica de Biologia – entenda Tipos de Sangue ABO e fator Rh https://blogdoenem.com.br/enem-2013-biologia-tipos-de-sangue/
EXERCÍCIOS COM RESOLUÇÃO
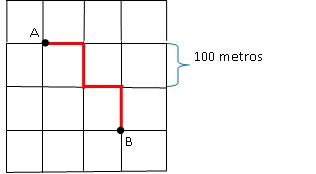
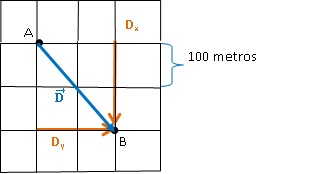
Numa cidade do interior de São Paulo, um novo bairro foi planejado para que todos os quarteirões sejam quadrados e suas ruas paralelas. A distância entre um par de ruas será de 100 m. Imagine um pedestre que realiza o percurso mostrado na figura, começando no ponto A e terminando sua trajetória no ponto B. Qual o módulo do vetor que representa a deslocamento (deslocamento vetorial) do pedestre?
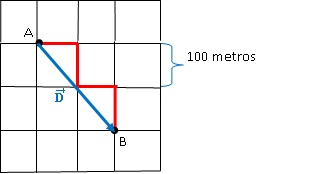
Para resolver esse problema, devemos lembrar a sobre trajetória e deslocamento. A trajetória é o que está traçado na figura, já o deslocamento é uma linha reta entre o ponto inicial e o ponto final. Esse então pode ser desenhado como um vetor: o vetor deslocamento representado na próxima figura.
Para calcular o módulo precisamos ter os valores do comprimento dos componentes do vetor, neste caso chamado de Dx e Dy. Pelo gráfico podemos ver que Dx= 200 metros e Dy= 200 metros.
Assim módulo do vetor deslocamento é:
Observe que pela figura inicial, também podemos dizer qual foi o distância percorrida (trajetória) pelo pedestre, foi de 400 metros.Fonte: Objetos Educacionais.
Aula elaborada pela Profª Danielle Fernandes A. dos Santos, do Gauss Pré-vestibular. Licenciada em Fíísica, mestre também em Física Experimental, hoje a professora estuda doutoramento em Ciência e Engenharia de Materiais pela Universidade Federal de Santa Catarina.