Análise combinatória é um dos conteúdos mais importantes para as questões de Matemática do Enem. Então, não deixe de conferir nosso resumo e resolver os exercícios!
Um dos assuntos que mais caem em Matemática no Enem é análise combinatória. Todos os anos aparece pelo menos uma questão. Então confira nosso resumo para relembrar o conteúdo e teste seus conhecimentos com exercícios sobre análise combinatória.
Resumo sobre análise combinatória
Em alguns sites da internet, para que tenhamos acesso aos conteúdos, é necessário a realização de um cadastro. Depois que essa etapa é concluída geralmente são fornecidos ao usuário um login e uma senha. Mas você deve estar pensando: “O que isso tem a ver com análise combinatória e com o princípio fundamental da contagem?” É que quando você cria uma senha, já está realizando uma operação de análise combinatória.
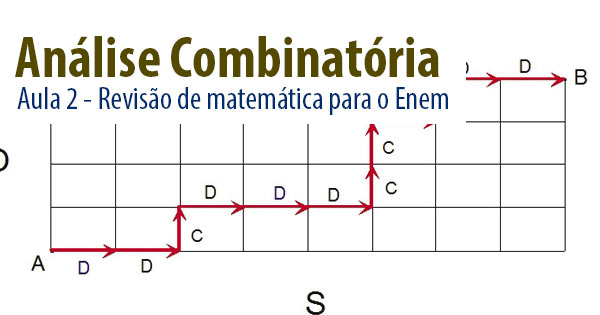
Imagine que você vai criar uma senha em um site e o sistema pede para colocar pelo menos uma letra maiúscula e um algarismo. Essas regras servem para multiplicar a quantidade de combinações possíveis. Outro exemplo: veja na imagem algumas combinações para um código ou senha que um site peça para você criar, com 4 letras maiúsculas e 3 algarismos. Olha só como ficariam alguns exemplos de senhas:
Sabendo que são utilizadas 26 letras do alfabeto e 10 algarismos (de 0 até 9), e que em cada senha não se repetem letras ou algarismos, quantas senhas diferentes podem ser formadas por este site?
Podemos responder a questão proposta anteriormente escrevendo todas as possibilidades e realizando a contagem das senhas. Este método é chamado de árvore de possibilidades. No entanto, escrever todas essas senhas pode ser trabalhoso.
Exemplo de análise combinatória
Imagine que uma moeda é lançada por três vezes seguidas. Vamos avaliar todos os resultados possíveis, sendo C (cara) e K (Coroa):
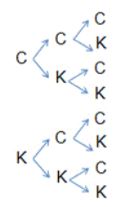
Por meio da análise do diagrama, podemos concluir que temos 8 opções diferentes de resultados para os 3 lançamentos. Situações que envolvem a contagem dos possíveis agrupamentos dos elementos de um ou mais conjuntos podem ser resolvidas com o Princípio Fundamental da Contagem ou Princípio Multiplicativo.
O Princípio Fundamental da Contagem é um método algébrico para determinar o número de possibilidades de escolha sem precisar descrevê-las. Se determinado acontecimento ocorre em n etapas diferentes, e se a primeira etapa pode ocorrer de k1 maneiras diferentes, a segunda de k2 maneiras, e assim sucessivamente, então o número total T de maneiras de ocorrer o acontecimento é dado por:
T = k1 . k2 . k3 … . kn
Por exemplo: se lançarmos simultaneamente um dado e uma moeda, quantos são os resultados possíveis? Como o dado possui 6 lados e a moeda duas, multiplicamos as possibilidades:
T = k1 . k2
T = 6 . 2
T = 12
Videoaula
Antes de partir para os exercícios sobre análise combinatória, assista à aula do professor Sarkis. Ele explica o passo a passo com exemplos de vários tipo de análise combinatória:
Exercícios sobre análise combinatória
Para saber como análise combinatória cai no Enem e nos vestibulares, confira a lista com 10 exercícios sobre o assunto. No final, você confere o seu número de acertos:
-
1. Pergunta
Cada uma das 12 pessoas inscritas para participar de um trabalho voluntário recebeu um crachá com um número de identificação distinto – de 1 a 12 – de acordo com a ordem de inscrição.
Desejando-se organizar grupos formados por três pessoas que não estejam identificadas por três números consecutivos, o número máximo possível de grupos distintos que se pode formar é -
2. Pergunta
Uma estudante ainda tem dúvidas quanto aos quatro últimos dígitos do número do celular de seu novo colega, pois não anotou quando ele lhe informou, apesar de saber quais são não se lembra da ordem em que eles aparecem.
Nessas condições, pode-se afirmar que o número de possibilidades para a ordem desses quatro dígitos é
-
3. Pergunta
Os números 258 e 179 têm seus algarismos escritos em ordem crescente. Os números 558 e 496 não têm seus algarismos escritos em ordem crescente. Quantos são os números de três algarismos no qual esses algarismos aparecem em ordem crescente?
-
4. Pergunta
Seis estudantes, entre eles Bruna e Caio, entraram em um auditório para assistir a uma palestra e escolheram uma fileira onde havia 8 poltronas vazias, uma ao lado da outra. Sabendo que Bruna e Caio querem sentar-se um ao lado do outro, o número de maneiras distintas de esses seis estudantes sentarem-se nessa fileira é
-
5. Pergunta
A figura apresenta uma foto do ícone do wi-fi (constituído de quatro elementos não conexos) que está pintado em vários pontos do calçadão da Praia de Ponta Verde, em Maceió.
Se a prefeitura decidir pintar os ícones com as cores da bandeira de Alagoas (branca, azul e vermelha), de modo que a cor repetida pinte dois elementos contíguos, quantos exemplares desse símbolo serão pintados de maneiras diferentes?
-
6. Pergunta
Quantos são os números naturais pares formados com quatro dígitos que têm pelo menos dois dígitos iguais?
-
7. Pergunta
Um tambor metálico, conforme representado na figura, será pintado com 7 faixas horizontais, cada uma delas com uma cor diferente, escolhida entre as seguintes opções: amarela, verde, azul, vermelho, lilás, preto e laranja.
Sabendo que a 1ª e a 4ª faixas deverão ser pintadas nas cores amarela e azul, respectivamente, e que a 7ª faixa não pode ser preta, é correto afirmar que o número de maneiras diferentes de pintar as 7 faixas desse tambor é
-
8. Pergunta
Uma comissão será composta pelo presidente, tesoureiro e secretário. Cinco candidatos se inscrevem para essa comissão, na qual o mais votado será o presidente, o segundo mais votado o tesoureiro e o menos votado o secretário. Dessa forma, de quantas maneiras possíveis essa comissão poderá ser formada?
-
9. Pergunta
Quantos números inteiros positivos pares, com três dígitos distintos, podemos formar com os algarismos 3, 4, 5, 6 e 7?
-
10. Pergunta
A capital dos gaúchos, oficialmente fundada em 26 de março de 1772, já foi chamada de Porto de Viamão. Atualmente, a também capital dos Pampas recebe o nome de PORTO ALEGRE.
Adicionando o número de anagramas formados com as letras da palavra ALEGRE ao de anagramas formados com as letras da palavra PORTO em que as consoantes aparecem juntas, obtemos _________ anagramas.
