Confira quais foram as questões mais difíceis do segundo dia do Enem 2025 e entenda por que esses itens exigiram mais interpretação.
Para muitos participantes, o segundo dia do Enem 2025 foi marcado por um aumento claro no nível de exigência. Algumas questões demandaram não apenas domínio de conteúdo, mas também estratégia, leitura cuidadosa e resistência após horas de prova.
Em Matemática, por exemplo, apareceram questões envolvendo geometria espacial, logaritmos e análise combinatória, temas considerados mais “travados” para muitos candidatos. Já nas Ciências da Natureza, embora muitos itens tenham cobrado conteúdos tradicionais, as questões consideradas mais difíceis exigiram leitura atenta e integração de conceitos, como nos itens de Física que trataram de circuitos elétricos com múltiplas variáveis ou aqueles de Química que trabalharam conceitos de equilíbrio químico em contexto.
Neste post, vamos focar nas questões mais difíceis desse segundo dia: aquelas que se destacaram pela demanda de raciocínio mais profundo, por várias etapas de interpretação ou pela exigência de combinar diferentes áreas do conhecimento. Bora lá?
Questão 1 – Ciências da Natureza
Resposta: D
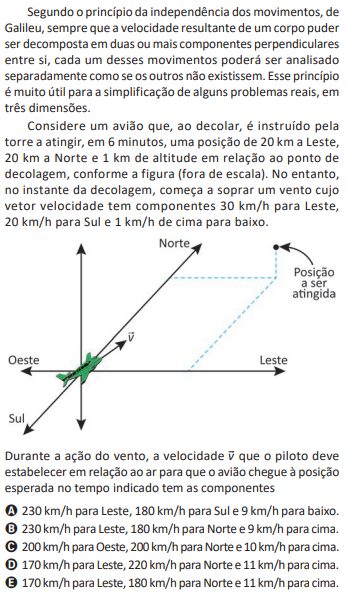
Resolução: conforme o enunciado, trata-se de uma composição de movimentos com três componentes independentes e simultâneos. Assim, podemos calcular as velocidades do avião em cada direção separadamente, considerando o intervalo de tempo de 6 min = 1/10 h nas três direções.
Na direção leste-oeste, como o avião se move para o leste e o vento sopra no mesmo sentido, a velocidade do vento deve ser somada à velocidade do avião. Assim, temos:
Vleste = 200 – 30
Vleste = 170 km/h
Na direção norte-sul, como o avião se move para o norte e o vento sopra no sentido contrário, a velocidade do vento deve ser subtraída da velocidade do avião. Assim temos:
Vnorte = 200 + 20
Vnorte = 220 km/h
Na direção vertical, como o avião se move para cima e o vento sopra no sentido contrário, a velocidade do vento deve ser subtraída da velocidade do avião. Assim, temos:
Vcima = 10 + 1
Vcima = 11 km/h
Questão equivalente em cada prova:
- Amarela – Questão 128
- Azul – Questão 126
- Cinza – Questão 121
- Verde – Questão 128
Questão 2 – Ciências da Natureza

Resposta: E
Resolução: no processo da fotossíntese, é necessária uma substância doadora de prótons e de elétrons. No fotossíntese anoxigênica, o doador é o H2S enquanto na fotossíntese oxigênica, o doador é a água.
Questão equivalente em cada prova:
- Amarela – Questão 121
- Azul – Questão 123
- Cinza – Questão 115
- Verde – Questão 132
Questão 3 – Matemática
Resposta: E
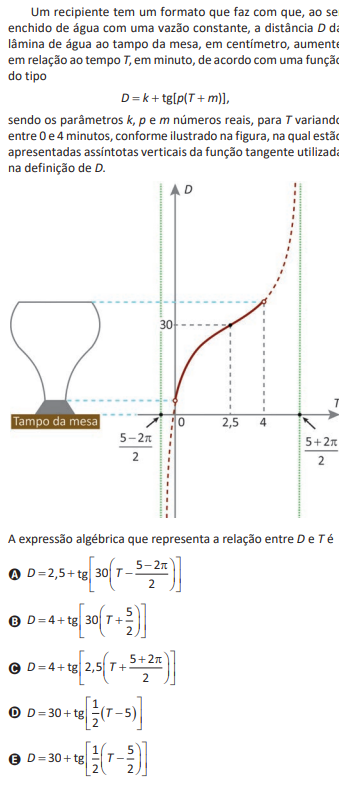
Resolução: os parâmetros k, p, m da função D = k + tg [p(T + m)] são responsáveis, respectivamente, pela translação vertical, dilatação/contração horizontal e translação horizontal do gráfico.
A função f(x) = tg(x) é periódica com período π, com o ponto (0, 0) sendo o ponto de inflexão (ponto de mudança da concavidade) do gráfico.
Note que, de acordo com o gráfico, o período da função dada é
Assim, como a função foi dilatada horizontalmente, temos que o parâmetro p é obtido fazendo
No gráfico apresentado, o ponto de inflexão (mudança da concavidade) ocorreu em D = 30, conclui-se que a função foi transladada verticalmente de 30 unidades, assim, k = 30.
Por fim, substituindo o ponto (5/2 ; 30) na expressão, temos:
Logo, a expressão algébrica que representa a relação entre D e T é:
Questão equivalente em cada prova:
- Amarela – Questão 159
- Azul – Questão 160
- Cinza – Questão 155
- Verde – Questão 164
Questão 4 – Matemática
Resposta: D
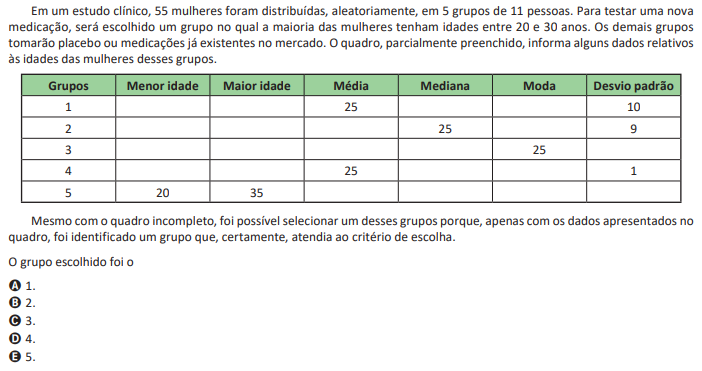
Resolução: note que, no grupo 4, como temos média de 25 e desvio padrão de 1, podemos concluir que:
Caso alguma das mulheres tenha idade maior do que 30, como por exemplo, 31, então teríamos que o termo referente a ela seria (25 – 31)² = 6² = 36, o que faria com que a soma fosse maior do que 11.
Caso alguma das mulheres tenha idade menor do que 20, como por exemplo, 19, então teríamos que o termo referente a ela seria (25 – 19)² = 6² = 36, o que também faria com que a soma fosse maior do que 11.
Com isso, qualquer outra idade maior do que 31 ou menor do que 19 faria com que a soma fosse maior ainda.
Assim, certamente as mulheres deste grupo têm idade entre 20 e 30 anos.
Questão equivalente em cada prova:
- Amarela – Questão 157
- Azul – Questão 165
- Cinza – Questão 158
- Verde – Questão 155
Questão 5 – Ciências da Natureza

Resposta: B
Resolução: o volume de gás produzido para um rendimento de 100% é:
Transformando o volume de gás em quantidade de matéria, tem-se:
De acordo com a equação química, a massa de bicarbonato de amônio é:
Questão equivalente em cada prova:
- Amarela – Questão 127
- Azul – Questão 125
- Cinza – Questão 120
- Verde – Questão 127
Questão 6 – Matemática

Resposta: A
Resolução: da condição P = 4 log [-k (t + 1) (t – 19) ≤ 10 obtemos:
Como k ≤ 102,5/-(t + 1) (t – 19), para obter o maior valor possível de k, precisamos do maior valor de:
Desenvolvendo, temos que D (t) = -t² + 18t + 19.
O maior valor ocorre em t = -18/(2 . -1) (abcissa do vértice da parábola)
∴ t = 9
Como 9 ∈ [0,10], então ele será o ponto de máximo, assim
Substituindo em 1, temos que o maior valor de k será
Questão equivalente em cada prova:
- Amarela – Questão 176
- Azul – Questão 172
- Cinza – Questão 169
- Verde – Questão 179
Questão 7 – Matemática

Resposta: E
Resolução: como Artur joga com dois dados de 1 a 6, os casos possíveis de combinações de resultados é dado por:
Artur:
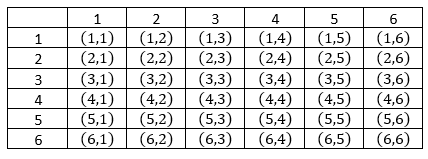
Já para o João, os casos são:

Assim, a probabilidade de João vencer é dada por
Logo, o jogador que tem a maior probabilidade de vitória é Artur com
Questão equivalente em cada prova:
- Amarela – Questão 169
- Azul – Questão 178
- Cinza – Questão 176
- Verde – Questão 172
Quer saber mais?
Entre no canal de WhatsApp do Curso Enem Gratuito! Lá, você recebe dicas exclusivas, resumos práticos, links para aulas e muito mais – tudo gratuito e direto no seu celular. É a chance de ficar por dentro de tudo o que rola no curso e não perder nenhuma novidade.

