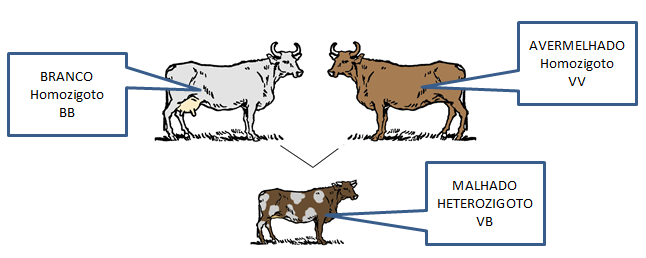
Veja os cálculos matemáticos para prever as probabilidades de um indivíduo herdar certas características hereditárias. Confira no Heredograma o fluxo da transmissão dos genes.
Então, para gabaritar as questões de genética e arrasar no vestibular, vamos revisar probabilidade aplicada à genética? Basicamente, as características hereditárias deterimadas pela genética que você e eu apresentamos são uma espécie de “loteria” em que temos a sorte (ou o azar) de herdarmos de nossos pais.
Por isso, para se dar bem nas questões deste conteúdo, não basta você ser fera nos conceitos básicos desse conteúdo! Saber o que é gene, fenótipo, genótipo e diferenciar os tipos de herança é essencial. Porém, estar afiado nos cálculos de probabilidades é vital para gabaritar as questões de genética & Características Hereditárias.
Aí você pensa: “- Poxa, já não bastam todas as questões de matemática? Ainda tenho que estudar isso também na biologia?” Pois é, querido (a) vestibulando (a), disso não dá para fugir! Mas, não se preocupe! Vamos te dar super dicas que vão te ajudar a tirar de letra as questões de probabilidade genética!
Regra da multiplicação ou regra do “e”
Você vai utilizar essa regra quando precisar calcular a probabilidade de dois eventos ocorrerem ao mesmo tempo, porém independentemente um do outro, ou seja, acontecimentos em que a possibilidade de um ocorrer não afeta a dos demais.
O jogo com duas moedas na genética
Vejamos a situação: tenho duas moedas e quero saber qual a probabilidade de que depois de lançadas ambas caiam com a face “cara” para cima. Para uma moeda é fácil: só há duas possibilidades: cara ou coroa. Então, eu tenho a possibilidade de ½ de sair “cara” em uma jogada.
Então se eu jogo as duas moedas ao mesmo tempo, cada uma terá ½ de ficar com a face “cara” voltada para cima, independentemente da outra, ou seja, uma não influencia no movimento da outra. Então, para que elas apresentem “cara” e “cara” eu preciso multiplicar a possibilidade das duas apresentarem esta face: ½ . ½ = ¼.
Podemos aplicar a mesma regra em genética. Por exemplo, imagine que uma questão do Enem cobre a seguinte resolução: qual a probabilidade de um casal heterozigoto para o albinismo ter um filho do sexo masculino albino?
Veja como resolver: o problema quer que você calcule duas características independentes: albinismo e sexo. Então, desse cruzamento, há ¼ de chances de o casal ter um filho albino e ½ de chance de ter um filho menino.
- Veja como resolver:
- Aplicamos a regra do “e” e multiplicamos as probabilidades isoladas de cada evento:
- ¼ albino . ½ menino
- Resultado = 1/8 de chances de nascer um menino albino.
Resumo sobre a Transmissão das Características Hereditárias
Confira agora com a professora Juliana Evelyn Santos, do canal do Curso Enem Gratuito, uma aula-sintese, que é um resumo super fácil sobre a Transmissão das Características Hereditárias.
Dicas básicas sobre as Características Hereditárias:
- No ser humano a determinação do sexo se dá por cromossomos especiais – os cromossomos sexuais.
- Para que uma pessoa seja do sexo feminino, ela precisa ter recebido um cromossomo sexual X de sua mãe e um cromossomo sexual X de seu pai.
- Já os indivíduos do sexo masculino, precisam receber um cromossomo X de sua mãe e um Y de seu pai para compor o seu par de cromossomos sexuais.
- Que tal visitar os Fundamentos da Genética?
- Se está difícil para você acompanhar esta aula, então, a dica é você revisar a 1ª lei de Mendel e o mecanismo de dominância completa.
Regra da adição ou regra do “ou” nas Catacterísticas Hereditárias:
Você irá utilizar esta regra quando dois acontecimentos são mutuamente exclusivos, ou seja, se um ocorre, o outro não acontece. Por exemplo: qual a possibilidade de sair o número 1 ou o número 5 em um lançamento de dado? Bem, isoladamente é fácil.
- Como resolver:
- Para que o dado caia com a face 1 virada para cima temos a probabilidade de 1/6 uma vez que o dado possui 6 lados.
- A mesma probabilidade ocorre para o número 5.
- Então, como eu quero saber a possibilidade de um acontecimento ou de outro, a probabilidade será calculada pela soma dos acontecimentos independentemente.
- Logo: 1/6 para que o dado caia com a face 1 somado com mais 1/6 para que o dado caia com a face 5
- Resultado = 2/6 = 1/3 de probabilidade que o dado caia com a face 1 ou 5 para cima.
Veja a aula de Probabilidade aplicada à Genética para entender mais
Agora, para aplicar à genética, vamos ao exemplo do professor Eduardo: Qual a probabilidade de um casal heterozigoto para o albinismo ter um filho menino ou albino? Para albinismo já sabemos que a proporção é de 1 para 4 (1/4) e para menino é de 1 para 2 (1/2).
Então, como as opções são excludentes, precisamos soma-las: ¼ de probabilidade de ser albino + ½ de probabilidade de ser menino = 6/8.
Outro exemplo: qual a probabilidade de um casal ter dois filhos: um do sexo feminino e outro do sexo masculino? Fique atento à “pegadinha” nesse caso – há duas maneiras de um casal ter um menino e uma menina: tendo primeiro uma menina e depois um menino ou tendo primeiro um menino e depois uma menina.
- Então, vamos calcular:
- Primeiro menina e depois menino (1/2 . ½ =1/4);
- Ou (+) primeiro menino e depois menina (1/2 . ½=1/4).;
- Logo: ¼ + ¼ = 2/4, ou ½.
Veja agora o Heredograma e a Transmissão das Características Hereditárias
Para compreender por que herdamos determinadas características genéticas, muitas vezes é fundamental que conheçamos o histórico biológico dos indivíduos afetados e de seus familiares.
Para isso é importante organizar as características investigadas em um esquema, ao qual chamamos de heredograma ou árvore genealógica. Os heredogramas costumam introduzir questões de genética nas provas de biologia dos vestibulares. Revise agora com a professora Juliana Evelyn Santos.
Quando tentamos descobrir os padrões de herança de determinada característica, geralmente realizamos cruzamentos testes, como Mendel realizou com suas ervilhas. Porém, isto não é possível quando pensamos na espécie humana. Por questões éticas, não podemos realizar cruzamentos dirigidos em seres humanos.
Por tais motivos, para entendermos os padrões de herança nos seres humanos, precisamos investigar o histórico familiar que cada indivíduo afetado pela característica que estamos estudando. Isto permite ao geneticista saber se a característica analisada é de fato herdada e de que maneira é herdada. E, para organizar os dados obtidos com esta investigação, organizamos um gráfico: o heredograma.
O heredograma consiste na representação de indivíduos, suas características e parentesco através de símbolos. Por exemplo, os indivíduos do sexo masculino, são representados por quadrados. Já as mulheres são indicadas por círculos.
Quando um indivíduo é afetado pela característica analisada, o símbolo aparece pintado. Casamentos são indicados por um traço ligando as laterais de dois símbolos.
Agora, veja o quadro abaixo com os principais símbolos de um heredograma: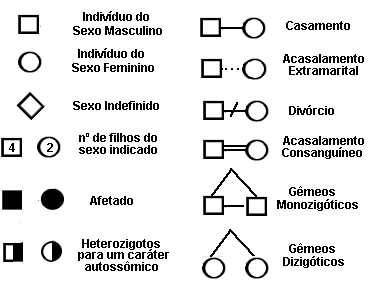 
Existem algumas regras durante a montagem de um heredograma que também pode ajudar você a entendê-lo:
- – Cada geração ocupa uma linha do heredograma, e é indicada por um algarismo romano (I, II, III, IV…).
- – Cada indivíduo é indicado por algarismos arábicos (1,2,3,4…) e sua numeração se inicia da esquerda para direita. A numeração começa de 1 em cada geração.
- – Os filhos de um casal são organizados por ordem de nascimento.
Os heredogramas adoram aparecer nos vestibulares e no Enem, pois eles permitem explorar uma série de conceitos genéticos e principalmente determinar o padrão de herança genética de uma característica.
Veja com a professora Juliana Evelyn Santos um resumo sobre o Heredograma:
Gostou da aula sobre o Heredograma? Assim você aprende o “caminho” da transmissão das características hereditárias. Agora, para saber analisá-los é essencial para você se dar bem nas questões de genética. Vamos, então, “esmiuçar” um exemplo?
Veja o heredograma a seguir: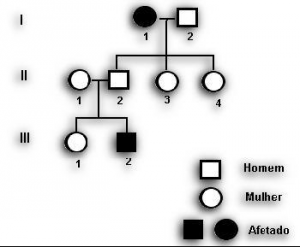 
A primeira coisa que você pode tentar descobrir ao observar este heredograma é se a característica analisada é condicionada por um gene recessivo ou dominante. Uma dica para ajuda-lo a descobrir: procure no heredograma casais fenotipicamente iguais que tiveram um ou mais filhos diferentes deles.
Se esta característica estiver presente, com certeza, meu querido, minha querida, a característica analisada é causada por um gene recessivo. Isto aconteceu, pois o caráter permaneceu oculto no casal e apareceu no filho.
Depois que você descobriu que tipo de gene condiciona a característica analisada, o segundo passo é mais simples: você deve localizar os homozigotos recessivos. No caso acima, como você sabe, a característica analisada é causada por um gene recessivo, por isso, os indivíduos afetados, indicados pelos símbolos pintados, são os indivíduos homozigotos recessivos.
Importante: Para finalizar a análise do heredograma, é importante lembrar-se de duas coisas:
1ª) Em um par de genes alelos, um veio do pai e o outro veio da mãe. Se o indivíduo analisado é homozigoto recessivo (possui dois alelos recessivos para um mesmo loco gênico), ele recebeu um gene recessivo de cada genitor.
2ª) Se um indivíduo é homozigoto recessivo, ele envia o gene recessivo para todos os seus filhos, uma vez que ele só tem esse tipo de alelo. Dessa forma, é fácil encontrar os outros genótipos dos outros integrantes do heredograma. Então, antes de finalizar o exercício, é importante que você saiba todos os genótipos presentes na árvore genealógica.
Sabendo disso, vamos pensar um pouco mais na árvore genealógica acima:
- – A primeira linha, ou geração, indica um casal em que a mulher é afetada.
- – Já a segunda linha, possui quatro indivíduos, em que nenhum é afetado pela característica analisada.
- – Na terceira geração vemos que há dois indivíduos, em que o do sexo masculino é afetado.
A partir disso, podemos notar duas informações importantes:
1 – *A característica é produzida por um gene recessivo, pois o casal 1-2 da segunda geração é fenotipicamente idêntico, porém produziu um filho com característica diferente.
2 – ** Provavelmente, esta não é uma herança ligada ao sexo, uma vez que está afetando igualmente ambos os sexos.
Agora que você já aprendeu a “desvendar” a simbologia dos heredogramas, que tal resolver os exercícios para testar seus conhecimentos?
Para isso, observe a imagem a seguir, e pense para compreender as Características Hereditárias:
Em 2006, a inglesa Kerry Richardson deu à luz a gêmeos com cor de pele e olhos completamente diferentes.
Em cima desse exemplo, vamos calcular uma possibilidade genética?
Qual a probabilidade de um casal de olhos castanhos heterozigoto para esta característica (lembre-se que o gene para olhos castanhos é dominante em relação ao gene para olhos azuis) ter dois filhos, um menino com olhos castanhos e uma menina com olhos azuis?
Resposta: Há duas possibilidades de esse casal ter essa combinação de filhos: primeiro uma menina de olhos azuis e depois um menino de olhos castanhos OU primeiro um menino de olhos castanhos e depois uma menina de olhos azuis. Então, em um cruzamento de heterozigotos para a cor de olhos temos a possibilidade de ¼ para o nascimento de uma criança de olhos azuis e ¾ de olhos castanhos. Para a determinação do sexo ½ para cada sexo. Então:
[(¼ olhos azuis e ½ menina) e (3/4 olhos castanhos e ½ menino)] OU [(3/4 olhos castanhos e ½ menino) e (¼ olhos azuis e ½ menina)] = [(1/4 . ½) . (3/4 . ½)] + [(3/4 . ½) . (1/4 . ½)] = [1/8 . 3/8] + [3/8 . 1/8] = 3/64 + 3/64 = 6/64 = 3 / 32.
Logo a probabilidade desta combinação ocorrer é de 3/32.
Veja mais dois exercícios sobre Características Hereditárias
1)(PUC-RS) A Doença de Huntington (DH) é uma anomalia autossômica com caráter dominante cuja manifestação ocorre na fase adulta, com uma progressiva perda do controle motor e problemas psiquiátricos como demência e distúrbios afetivos.
No heredograma a seguir, os indivíduos afetados por DH estão indicados em negro.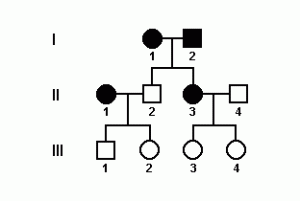
As afirmativas abaixo se referem aos possíveis genótipos dos indivíduos indicados no heredograma.
- Assinale, nos parênteses, V para as verdadeiras e F para as falsas.
- ( ) Os indivíduos I-1, I-2, II-1 e II-3 são homozigotos.
- ( ) Os indivíduos II-1 e II-3 são heterozigotos.
- ( ) Os indivíduos II-2 e II-4 são heterozigotos.
- ( ) Os indivíduos III-1, III-2, III-3 e III-4 são homozigotos.
A sequência correta de preenchimento dos parênteses, de cima para baixo, é
- a) F – V – F – V
- b) F – V – V – F
- c) V – F – V – F
- d) V – F – F – V
- e) V – F – V – V
Resposta: alternativa A. O casal I-1 I-2 teve um filho com fenótipo igual ao seu e outro diferente. Logo, este casal não pode ter homozigose para a característica analisada. Sendo assim, os indivíduos afetados podem ser homozigotos dominantes ou heterozigotos. Já os indivíduos não afetados, serão homozigotos. Neste heredograma, a partir dos dados analisados, podemos dizer que a característica avaliada é produzida a partir de um gene dominante.
2) (UFPR) Na genealogia a seguir, os indivíduos assinalados com preto apresentam uma anomalia determinada por um gene dominante.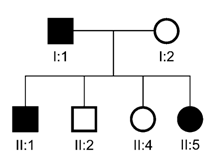
Analisando essa genealogia, é correto afirmar:
- a) Todos os indivíduos afetados são homozigotos.
- b) Todos os indivíduos não afetados são heterozigotos.
- c) Apenas o indivíduo I:1 é heterozigoto.
- d) Apenas os indivíduos I:1; II:1 e II:5 são heterozigotos.
- e) Apenas os indivíduos I:1 e I:2 são homozigotos.
Resposta: alternativa D.
