Inequações do 2º grau, inequação produto e quociente

Nesta aula, serão abordados os mais diversos tipos de inequações, suas definições, restrições e resoluções. Venha se preparar para fazer uma prova show de matemática no Enem!

Inequações do 2° Grau:

As inequações são expressões matemáticas que utilizam, na sua formatação, os seguintes sinais de desigualdades:
>: maior que
<: menor que
≥: maior ou igual
≤: menor ou igual
≠: diferente

As inequações do 2º grau são resolvidas utilizando o teorema de Bháskara. O resultado deve ser comparado ao sinal da inequação, com o objetivo de formular o conjunto solução.

São denominadas de inequações do 2° grau as inequações do tipo:

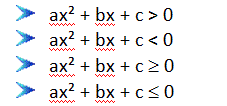
Para resolvermos uma inequação do Segundo grau devemos estudar o sinal da função correspondente equação.

1. Igualar a sentença do 2° grau à zero;
2. Localizar e (se existir) as raízes da equação no eixo x.
3. Estudar o sinal da função correspondente, tendo-se como possibilidades:

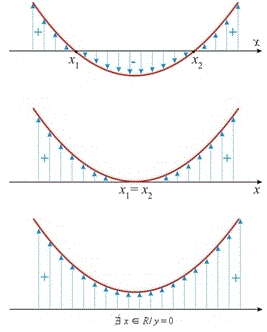
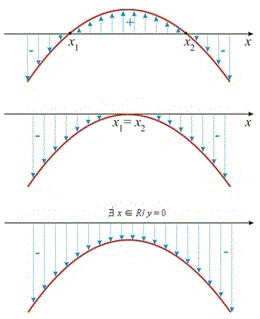
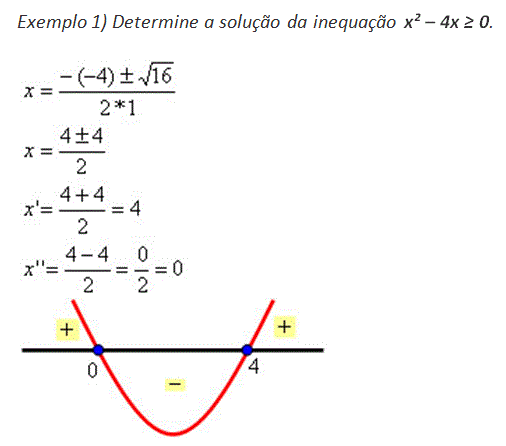
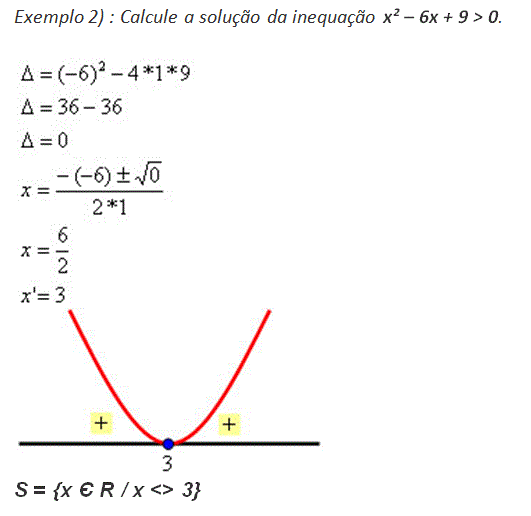
Antes de continuar, veja esta videoaula com exemplos para entender como resolver inequações do segundo grau:

Inequação Produto 

Resolver uma inequação produto consiste em encontrar os valores de x que satisfazem a condição estabelecida pela inequação. Para isso utilizamos o estudo do sinal de uma função. Observe a resolução da seguinte equação produto: (2x + 6).( – 3x + 12) > 0.
Vamos estabelecer as seguintes funções: y1 = 2x + 6 e y2 = – 3x + 12

Determinando a raiz da função (y = 0) e a posição da reta (a > 0 crescente e a < 0 decrescente).

y₁ = 2x + 6
2x + 6 = 0
2x = – 6
x = –3

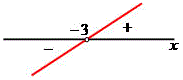
y₂ = – 3x + 12
–3x + 12 = 0
–3x = –12
x = 4

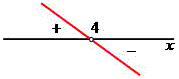
Verificando o sinal da inequação produto (2x + 6).(– 3x + 12) > 0. Observe que a inequação produto exige a seguinte condição: os possíveis valores devem ser maiores que zero, isto é, positivo.

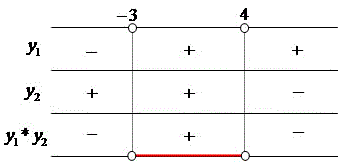
Através do esquema que demonstra os sinais da inequação produto y1*y2, podemos chegar à seguinte conclusão quanto aos valores de x: {x Є R / –3 < x < 4}

Inequação quociente

Na resolução da inequação quociente utilizamos os mesmos recursos da inequação produto, o que difere é que, ao calcularmos a função do denominador, precisamos adotar valores maiores ou menores que zero e nunca igual a zero. Observe a resolução da seguinte inequação quociente:

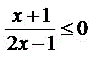
Resolver as funções y₁ = x + 1 e y₂ = 2x – 1, determinando a raiz da função (y = 0) e a posição da reta (a > 0 crescente e a < 0 decrescente).
y₁ = x + 1
x + 1 = 0
x = –1

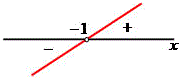
y₂ = 2x – 1
2x – 1 = 0
2x = 1
x = 1/2

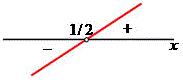
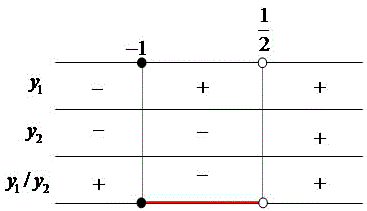
Com base no jogo de sinal concluímos que x assume os seguintes valores na inequação quociente:

{x Є R / –1 ≤ x < 1/2 }

Os textos e exemplos acima foram preparados pela professora Jaceli Eccher para o Blog do Enem. Jaceli é formada em Matemática habilitação Licenciatura pela Universidade Federal de Santa Catarina com Especialização no ensino de Ciências pelo Instituto Federal de Santa Catarina. Facebook: https://www.facebook.com/Jacelieccher