Potenciação, radiciação e notação científica

Você lembra de Potenciação e Radiciação? Veja aqui um resumo para o Enem e o Vestibular.

Potenciação

Potenciação é a operação matemática que resulta da multiplicação de um mesmo número n vezes. Algumas propriedades importantes devem ser relembradas:
a) aⁿ ⋅ a ^m = a^n+m

b)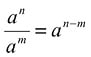

c) (aⁿ)^m = a ^n.m

d) (a⋅b)ⁿ = aⁿ⋅bⁿ

e)

f)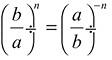

g)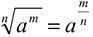

Radiciação

A radiciação é uma operação unária oposta à potenciação (ou exponenciação). Destacam-se algumas propriedades importantes, a saber:

a)

b)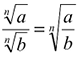

c)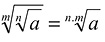

d)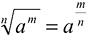

Notação científica

Notação científica, também denominada padrão ou notação em forma exponencial, é uma forma de escrever números que acomoda valores demasiadamente grandes (100000000000) ou pequenos (0,00000000001) para serem adequadamente escritos na forma convencional.

aⁿ ⋅ 10ⁿ 1 ≤ a <10

n &#8712 Z

Exercício resolvido:

(G1 – EPCAR [CPCAR], 2011) Simplificando-se a expressão

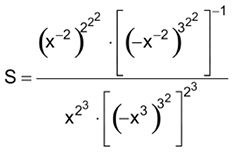
onde x ≠ 0, x ≠ 1 e x ≠ -1, obtém-se

a)-x^-94

b) x⁹⁴

c) x^-94

d) -x⁹⁴

Gabarito: A

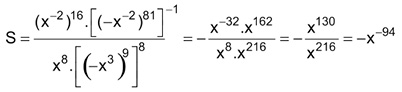
Veja nossa aula sobre radiciação e prepare-se para as provas!

Exercícios:

Questão 1

(G1 – CFTMG, 2010) Segundo estimativas do IBGE, em 2009, o Brasil tinha, aproximadamente, 190 milhões de habitantes espalhados pelas suas 27 unidades da Federação e 5.565 municípios. A tabela seguinte mostra o número aproximado de habitantes em algumas capitais brasileiras.

Capitais	Nº de habitantes
Belo Horizonte	2.400.000
Brasília	2.600.000
Rio de Janeiro	6.000.000
São Paulo	11.000.000

Com base nesses dados, é correto afirmar que, aproximadamente ………………., habitantes estão distribuídos em ………………. .

A opção que completa corretamente as lacunas acima é:

a) 1,68 x 10⁸, 5.561 municípios.

b) 2,45 x 10⁷, 5.561 municípios.

c) 7,52 x 10⁶, Belo Horizonte e Brasília.

d) 7,10 x 10⁶, Belo Horizonte e São Paulo.

Questão 2

(PUCSP, 2007) A tabela a seguir permite exprimir os valores de certas grandezas em relação a um valor determinado da mesma grandeza tomado como referência. Os múltiplos e submúltiplos decimais das unidades derivadas das unidades do Sistema Internacional de Unidades (SI) podem ser obtidos direta ou indiretamente dos valores apresentados e têm seus nomes formados pelo emprego dos prefixos indicados.

Nome	Símbolo	Fator pelo qual a unidade é multiplicada
tera	T	1012 = 1000000000000
giga	G	103 = 1 000 000 000
mega	M	106 = 1 000 000
quilo	k	103 = 1 000
hecto	h	102 = 100
decta	da	10 = 10
deci	d	10-1 = 0,1
centi	c	10-2 = 0,01
mili	m	10-3 = 0,001
micro	µ	10-6 = 0,000 001
nano	n	10-9 = 0,000 000 001
pico	p	10-12 = 0, 000 000 000 001

Assim, por exemplo, se a unidade de referência fosse o metro (m), teríamos: 28.000 μm (micrômetros) = 28.000 × 10^-6 m (metros) = 0,028 m (metros).

Considerando o bel (b) como unidade de referência, a

expressão 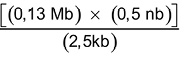é equivalente a:

a) 0,0026 cb

b) 0,026 ìb

c) 0,26 kb

d) 2,6 db

e) 26 pb

Questão 3

(G1 – CPS 2005) Um grupo de alunos do Ensino Técnico realizou um trabalho de pesquisa para determinar a área da superfície do corpo humano de jovens de 15 a 20 anos. Chegaram à conclusão de que a área varia, aproximadamente, de acordo com a fórmula matemática S = 0,12.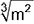, em que S é a área (m²) e m a massa do corpo humano (kg). A área aproximada da superfície do corpo de um aluno de massa 70 kg, em m² é:

a) 3,0

b) 2,5

c) 2,0

d) 1,5

e) 1,0

Questão 4

(UFRN, 2004) Uma calculadora apresentava, em sua tela, o resultado da soma dos gastos do mês realizados por um pai “coruja” que permitiu a seu filho apertar algumas teclas, alterando esse resultado. O pai observou que o menino havia apertado as teclas uma única vez, na ordem mostrada na figura 1.

Para recuperar o resultado que estava na tela, o pai deverá apertar as teclas:

Questão 5

(UFMG, 2003) O valor da expressão (a^-1 + b^-1)^-2 é:

a) [ab/(a + b)²]

b) [ab/(a² + b²)²]

c) a² + b²

d) [a²b²/(a + b)²]