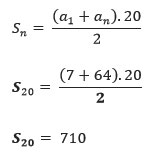Progressão Aritmética (PA): resumo de Matemática Básica

Você lembra do conceito de  Progressão Aritmética, a famosa PA? – Hora de revisar, porque sempre cai. É fácil, mas exige um pouco de atenção. Veja os resumos e acompanhe os exercícios resolvidos.

Vamos começar pelo começo: Progressão Aritmética é toda sequência numérica em que a diferença entre um termo e o seu antecedente é constante. A essa constante dá-se o nome de razão ‘r’ da PA.  Complicou ou entendeu de primeira?

Veja esta outra forma de descrever o que é uma Progressão Aritmética: Uma progressão aritmética (abreviadamente, P. A.) é uma sequência numérica em que cada termo, a partir do segundo, é igual à soma do termo anterior com uma constante. O número é chamado de razão ou diferença comum da progressão aritmética. (fonte Wiki)

Para sair da complicação, vamos ao exemplo, que descomplica geral.  Acompanhe a solução da seguinte Progressão Aritmética:

• Observe esta PA (1, 5, 9, 13, 17, …)
• Veja que 5-1 = 9-5 = 13-9 = 17-13 = 4
• Assim, temos que a razão dessa PA é igual a 4
• Ou seja, r = 4

Veja outro outro exemplo de Progressão Aritmética:

• PA (20, 18, 16, 14, …)
• Aqui também há diferença constante entre qualquer termo e seu antecedente. Veja:
• 18-20 = 16-18 = 14-16 = -2 = r
• Portanto:
• R=-2

Aula Gratuita para começar sua revisão de Progressão Aritmética com o prof. Lucas:

Valeu o resumo? Veja mais exercícios resolvidos.

Só mais este problema,  para você não esquecer:

• PA (5, 5, 5, 5, …)
• Neste caso, r = 0.

Classificação da Progressão Aritmética:

• PA Crescente⇒ r > 0
• PA Decrescente ⇒ r < 0
• PA Constante ⇒ r = 0

Numa PA sempre se encontram as seguintes propriedades:

Propriedades da Progressão Aritmética:

P1) A soma dos termos extremos é igual à soma dos termos equidistantes dos extremos.

P2) Um termo central é igual à média aritmética dos equidistantes.

Só vendo para crer? Então observe confirmação dessas propriedades no exemplo abaixo:

PA (1, 4, 7, 10, 13, 16, 19)

P1) 1+19 = 4 +16 = 7+13

P2)

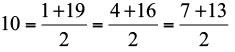
Fórmula do termo geral de uma PA, você lembra o que é?

É uma formula que fornece todos os termos da sequência, por exemplo:

Supondo que nosso interesse seja obter o 51^o da PA (2, 5, 8, …), seria muito prático usar uma fórmula para obtê-lo, não é mesmo?

Vamos à fórmula:

a_n=a₁ +(n-1).r

Considere uma PA qualquer

Voltando à pergunta “Qual o 51^o da PA (2, 5, 8, …)?”, observe que:

a₅₁ = a₁ + (n-1)r

a₅₁ = 2 + (51-1).3

a₅₁ = 152

E se você precisar calcular todos os termos de uma PA? Vamos lá…

Você pode utilizar a fórmula da soma dos termos de uma PA:

Veja um exemplo:

Qual a soma dos 20 primeiros termos da P.A (7,10,13…)?

Primeiramente você precisa saber qual o valor do vigésimo termo da PA, para tanto, usaremos a fórmula do termo geral:

a₂₀ = a 1 + (n-1).r
a₂₀ = 7 + (20-1).3
a₂₀ = 64

Agora, a soma dos termos:

Resumo de Progressão Geométrica

Pra você gabaritar geral no Enem, veja também o resumo básico sobre Progressão Geométrica, a famosa PG:

Exercícios sobre Progressão Aritmética. Veja:

Você consegue resolver este exercício abaixo? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!

(Enem, 2011) O número mensal de passagens de uma determinada empresa aérea aumentou no ano passado nas seguintes condições: em janeiro foram vendidas 33.000 passagens; em fevereiro, 34.500; em março, 36.000. Esse padrão de crescimento se mantém para os meses subsequentes.

Quantas passagens foram vendidas por essa empresa em julho do ano passado?

a) 38 000
b) 40 500
c) 41 000
d) 42 000
e) 48 000

Resposta:d

Os textos e exemplos de apresentação desta aula foram preparados pela professora Munique Dias para o Blog do Enem. Munique é formada em química pela UFSC, tem mestrado e atualmente cursa o doutorado em Engenharia. Química, também pela UFSC. Facebook: https://www.facebook.com/MuniqueDias .