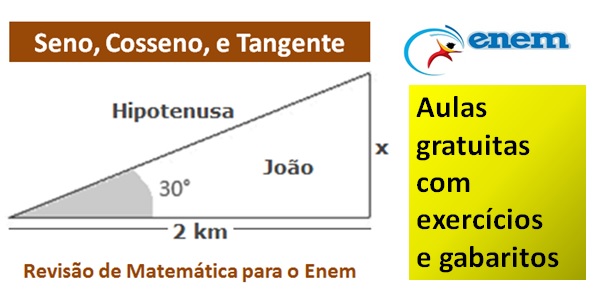
Aprenda mais sobre Seno, Cosseno e Tangente aqui no Blog do Enem com aulas e exercícios da Khan Academy e o aplicativo Geogebra. Depois dessa aula do professor Davi Rissetti você estará pronto para enfrentar a Matemática o Enem e os Vestibulares mais concorridos.
Seno, Cosseno, e Tangente. Você esta em dia com as definições, conceitos e os cálculos? Questões assim pouca gente acerta. Se você conseguir, soma pontos importantes. Vamos lá? Veja a Introdução e siga adiante. Tudo começa com o Teorema de Pitágoras:
Você já deve estar familiarizado com o estudo das relações métricas em um triângulo retângulo. É claro que você deve se lembrar de que um triângulo possui três lados que podem se relacionar compondo, inclusive, o famoso: TEOREMA DE PITÁGORAS.
Esse teorema é crucial para os estudos de Matemática para o Enem. Você sabe tudo sobre o Teorema de Pitágoras?Se você respondeu ‘SIM’, que sabe tudo sobre o Teorema de Pitágoras, então avence uma casa.
Porém, só avance se lembrar mesmo as relações entre os Catetos e a Hipotenusa, e os cálculos de ângulos envolvendo os triângulos retângulos.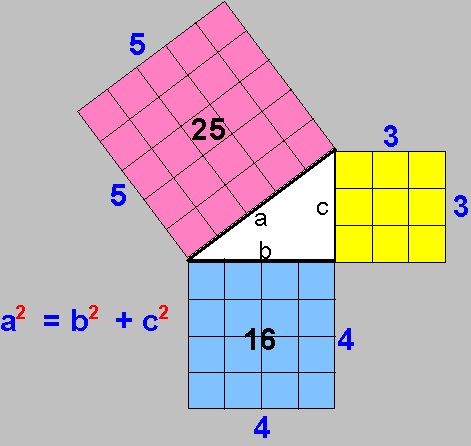 Revise o Teorema de Pitágoras
Revise o Teorema de Pitágoras
Mas, se você têm dúvidas ou precisa recordar um pouco sobre o Teorema de Pitágoras a dica do Blog do Enem é você dar uma parada aqui de 15 minutos para revisar este conteúdo numa aula especial com o professor
Agora, vamos à aula de Seno e Cosseno
Pois bem, já que você revisou ou relembrou o Teorema de Pitágoras, é hora de mergulhar mais fundo e aprender (ou lembrar) Seno e Cosseno. Vamos considerar o triângulo da figura abaixo: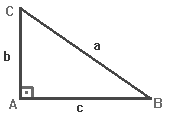
Em um triângulo retângulo, temos dois lados que formam ângulos com a hipotenusa, então para não criar confusões, denomina-se o lado sempre tomando como referência o ângulo ao qual ele está relacionado. Para isso, acompanhe a tabela abaixo:
|
Ângulo |
Lado oposto |
Lado adjacente |
|
C |
AB = c |
AC = b |
|
B |
AC = b |
AB = c |
O lado adjacente, que citei na tabela acima, é o lado que descreve o ângulo junto com a hipotenusa. Agora, treine com os exercícios abaixo a aplicação do teorema de Pitágoras, procure destacar em cada um dos exercícios resolvidos qual é o nome de cada lado (se é oposto ou adjacente) em relação aos ângulos da figura.
Veja a Lei do Seno
- A lei dos senos é usada quando temos um triângulo e sabemos os valores de dois ângulos e um lado. Quando temos os valores de dois lados e um ângulo, usamos a lei dos cossenos.
- A lei dos senos diz o seguinte: se eu tenho um lado qualquer e divido pelo seno do ângulo que enxerga esse lado, isso é igual que um outro lado dividido pelo seno do seu ângulo.
- Ou seja, a fórmula da lei dos senos é: a / sen(A) = b / sen(B) = c / sen(C). Para aplicar a lei dos senos, temos que definir qual ângulo está associado a qual lado para montar a fórmula.
- ntão, na figura do triângulo, é interessante estipular qual será lado a e o ângulo A, assim como o lado b e o ângulo B, e o lado c e o ângulo C.
- Assim, pode-se montar a fórmula da lei dos senos substituindo os valores colocados pelo exercício. Para ficar mais fácil de visualizar, no vídeo, o professor Lucas faz uma demonstração de como aplicar a lei dos senos em um exercício! Veja acima.
Veja a Lei do Cosseno
Acompanhe com o professor Lucas Borguesan, a Lei doCosseno.
- A lei dos cossenos é usada quando temos um triângulo e só sabemos os valores de dois dos seus lados e o valor de um dos ângulos.
- Se for um triângulo retângulo, ou seja, um triângulo com um ângulo reto, seria possível resolver o problema com o Teorema de Pitágoras.
- Contudo, em outros tipos de retângulos é preciso aplicar a lei dos cossenos. A fórmula da lei dos cossenos, inclusive, é bastante parecida com o Teorema de Pitágoras, então é importante prestar atenção para não confundir as fórmulas.
- A fórmula da lei dos cossenos é a² = b² + c² – 2.b.c.cos(A)
- Na hora de aplicar a lei dos cossenos, lembre-se de que a “hipotenusa” é o lado oposto ao ângulo cujo valor é conhecido. Ou seja, o temos o valor do lado a e o valor do ângulo A, cujo cosseno precisamos descobrir caso o enunciado do exercício não informar.
Agora que você já entendeu o processo acima, vamos trabalhar a ideia principal desse nosso post. Para isso, vamos contextualizar um pouco a motivação deste estudo.
Processo histórico
A essa altura, você já deve saber que a Matemática sempre andou de mãos dadas com a Astronomia, Agrimensura e as Navegações. E, por conta dessa proximidade, muitos dos problemas que surgiram com essas ciências utilizaram recursos da Álgebra e Geometria para encontrar suas respectivas soluções.
Por exemplo, no ENEM de 2009, caiu uma questão interessante que envolvia três irmãos que dividiriam uma herança com uma área de extração de ouro delimitada por uma região circular. Se tomarmos emprestado uma parte desse problema, teríamos a seguinte figura geométrica:
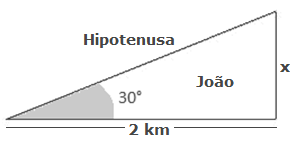
E, para encontrar o valor do lado X deste triângulo usaremos as relações trigonométricas, pois com elas podemos associar as razões entre dois lados (oposto e adjacente) a uma medida específica de cada ângulo. No nosso caso, podemos fazer três associações:
|
Ângulo |
1ª Razão |
2ª Razão |
3ª Razão |
|
30° |
x/hipotenusa |
2/hipotenusa |
x/2 |
Para a 1ª razão, damos o nome de SENO. Já para a 2ª razão, damos o nome de COSSENO e para a 3ª razão, damos o nome de TANGENTE. Agora, você deve estar se perguntando: porque esses nomes? E como eu vou guardar quem é o que?
Primeiro, a história da matemática possui alguns fatos interessantes. Por volta de 500 d.C. os hindus chamavam o nosso atual SENO de JIVA. Que ao ser traduzido pelos árabes (que tinham o costume de escrever somente as consoantes) ficou conhecido como JAIB, ao invés de JIBA (denominação correta segundo o conceito hindu). E, este quando foi traduzido para o latim, chegou até nós como SINUS. Se quiser saber mais sobre este processo histórico e a origem dos outros nomes fica a dica abaixo.
Dicas de Trigonometria:
Respondendo a sua provável segunda inquietação, é muito simples guardar qual razão está relacionada com qual lado, veja:
![]()
Existe até uma brincadeira que fazemos em sala de aula para vocês guardarem essas siglas, imagine que eu estou parado em frente à escola em que vou aplicar a prova do ENEM. Ao olhar no relógio, vejo que estou atrasado, então, pego a minha coca e saio correndo, no caminho tomo um tombo daqueles e chego todo molhado na sala de aula, para justificar a vocês digo:
“CORRI e CAÍ com COCA!” à (Cohi, Cahi, Coca).
Dica do Blog: Conheça mais sobre o processo histórico e enriqueça suas ideias trigonométricas em http://ecalculo.if.usp.br/historia/historia_trigonometria.htm E veja também uma aula completa sobre o Círculo Trigonométrico one você aprende a utilizar os eixos X e Y, e os Quatro Quadrantes do Círculo para fazer os cálculos necessários.
Aulas Khan Academy de Seno e Cosseno:
Veja na Khan Academy algumas aplicações para Seno, Cosseno e Tangente:
Assista essas aulas na plataforma da Khan Academy: http://goo.gl/e5dsnQ E veja esta também, sobre o Teorema de Pitágoras: http://goo.gl/F0VcZM
Dica 3: Para explorar melhor o comportamento da razão SENO, aproveite esse applet desenvolvido por mim através do Geogebra (software gratuito de geometria dinâmica) aqui no blog do ENEM. Você pode utilizá-lo logo abaixo ou neste link http://ggbtu.be/mvKiLAW9r
Veja mais sobre essa parte introdutória de trigonometria com a Khan Academy e fique preparado para o ENEM ou Vestibulares.
Veja esta aula na plataforma da Khan: http://goo.gl/qcdwfO
Aqui você poderá explorar outras informações mais relevantes sobre as razões trigonométricas na forma de exercícios: http://goo.gl/878zKf
Não esqueça que a tabela trigonométrica passada no vídeo acima e trabalhada em alguns exercícios leva em consideração somente os três ângulos notáveis, mas que existem outros infinitos ângulos que possuem cada um suas respectivas razões trigonométricas.
Confira a tabela abaixo: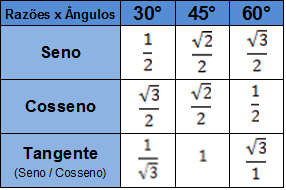
Desafios de Seno e Cosseno
1 – (UFPI) Um avião decola, percorrendo uma trajetória retilínea, formando com o solo um ângulo de 30° (suponha que a região sobrevoada pelo avião seja plana). Depois de percorrer 1.000 metros, a altura atingida pelo avião, em metros, vale quanto?
2 – (PUCCAMP) Uma pessoa encontra-se num ponto A, localizado na base de um prédio, conforme mostra a figura adiante. Se ela caminhar 90 metros em linha reta, chegará a um ponto B, de onde poderá ver o topo C do prédio, sob um ângulo de 60°. Quantos metros ela deverá se afastar do ponto A, andando em linha reta no sentido de A para B, para que possa enxergar o topo do prédio sob um ângulo de 30°?
a) 150 b) 180 c) 270 d) 300 e) 310
Resolva mais exercícios de Trigonometria com a Khan Academy e vá confiante para a prova do ENEM ou Vestibular: http://goo.gl/AiaSoo
Gabarito: 1) A altura será de 500 metros; 2) C
Autoria de Davi Rissetti
Este post é resultado da parceria da Fundação Lemann com o Blog do Enem – www.fundacaolemann.org.br