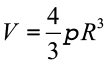Esfera – Conceitos e cálculos no resumo de matemática

Considerando a rotação completa de um semicírculo em torno de um eixo e, a esfera é o sólido gerado por essa rotação. Assim, ela é limitada por uma superfície esférica e formada por todos os pontos pertencentes a essa superfície e ao seu interior.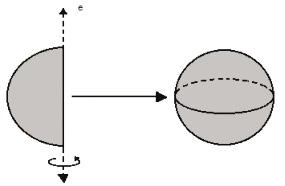

Ôpa, complicou pra você? Foi tudo rápido demais? Então, vamos descomplicar com um resumo de introdução do professor professor de matemática Lucas Borguezan, do canal do Curso Enem Gratuito.

Conceitos e Cálculos da Esfera

Valeu pra você? Agora ficou mais fácil. Vamos continuar, então.

Elementos da Esfera

• R = raio = distância do centro da esfera até a superfície.
• D = diâmetro = 2R

Relações da Esfera

Área da superfície esférica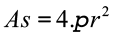

Volume da esfera

Dica 1 – Tire todas as suas dúvidas sobre o Tronco de Pirâmide e Tronco de Cone em mais esta aula de revisão para prova de Matemática Enem – https://blogdoenem.com.br/tronco-de-piramide-e-cone-matematica-enem/

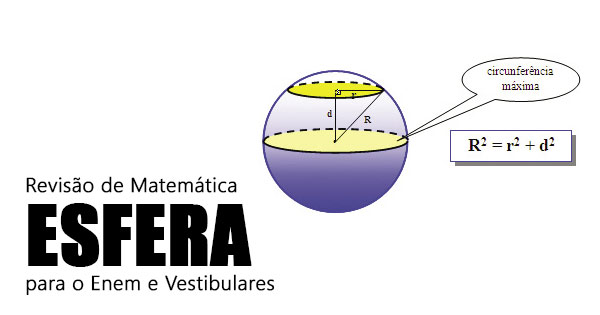
Secção da Esfera

Uma esfera de raio R pode ser cortada por um plano a uma distância d em relação ao seu centro. Esse corte forma uma área circular de raio r, conforme a figura abaixo.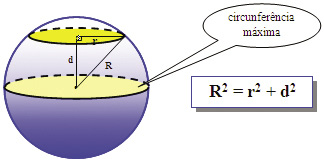

Relações

 

Saiba mais sobre Esfera nesta aula do canal Curso Enem Gratuito, com o professor Sérgio, disponível no Youtube. Após assistir, revise o que você aprendeu respondendo aos nossos desafios!

.

Veja o que é um Tronco de Cone, e como

Confira agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, como fazer os cálculos para o Tronco de Cone:

Desafios e cálculos sobre a Esfera

Questão 01

Sabendo que a área de uma superfície esférica é 16 π cm², qual o raio da esfera?

a) 3cm

b) 5cm

c) 7cm

d) 2cm

e) 4cm

Dica 2 – Relembre tudo sobre as características dos Cones em mais esta aula preparatória para a prova de Matemática Enem. Estude com a gente, o Enem está chegando! – https://blogdoenem.com.br/cones-matematica-enem/

Questão 02

Uma superfície esférica de raio 13cm é cortada por um plano situado a uma distância de 12cm do centro da superfície esférica, determinando uma circunferência. O raio dessa circunferência, em centímetros, é:

a) 5

b) 4

c) 3

d) 2

e) 6

Dica 3 – Relembre sobre o conceito e os tipos de Cilindros nesta aula preparatória para a prova de Matemática Enem. Estude conosco e fique preparado para o Exame! – https://blogdoenem.com.br/cilindro-matematica-enem/

Questão 03

Um sorveteiro vende sorvetes em casquinhas de biscoito que têm a forma de cone de 3cm de diâmetro e  6cm de profundidade. As casquinhas são totalmente preenchidas de sorvete e, ainda, nelas é superposta uma meia bola de sorvete de mesmo diâmetro do cone. Os recipientes onde é armazenado o sorvete têm forma cilíndrica de 18cm de diâmetro e 5cm de profundidade. Determine o número de casquinhas que podem ser servidas com o sorvete armazenado em um recipiente cheio.

a) 36

b) 40

c) 45

d) 50

e) 52

Questão 04

A tira seguinte mostra o Cebolinha tentando levantar um haltere, que é um aparelho feito de ferro, composto de duas esferas acopladas a um bastão cilíndrico.

Suponha que cada esfera tenha 10,5cm de diâmetro e que o bastão tenha 50cm de comprimento e diâmetro da base medindo 1,4cm. Se a densidade do ferro é 7,8g/cm³, quantos quilogramas, aproximadamente, o Cebolinha tentava levantar? (Use: π = 22/7)

a) 8

b) 16

c) 15

d) 12

e) 10

Questão 05

A área da superfície coberta de água corresponde a aproximadamente 3/4 da superfície da Terra. Considerando que a Terra seja uma esfera de raio 6.370km, determine a área da superfície da Terra que é coberta pela água.

a) 382.234.398 km²

b) 420.120.300 km²

c) 285.465.213 km²

d) 345.654.124 km²

e) 410.879.523 km²