Relembre tudo sobre as características dos Cones em mais esta aula preparatória para as provas de Matemática no vestibular e no Enem. Estude com a gente e chegue para gabaritar nas provas.
Cones caem com frequência nas questões avançadas de matemática. Aprenda a fazer os cálculos de área, volume, base, eixo, Geratriz, e etc.
Considere uma região plana limitada por uma curva suave (sem quinas), fechada e um ponto P fora desse plano. Chamamos de cone ao sólido formado pela reunião de todos os segmentos de reta que têm uma extremidade em P e a outra num ponto qualquer da região. Veja nesta aula como fazer os cálculos para resolver questões de matemática no Enem e nos vestibulares sobre os Cones.
Em nosso cotidiano, encontramos diversos objetos na forma cônica. Se você parar um segundo para pensar logo virão imagens de cones na sua mente. Vamos lá… Sorvete na casquinha? Sim, é um cone. Cartucho de amendoim, daqueles enrolados em papel de pão? Sim, é um cone.
Os ‘pirulitos’ de sinalização utilizados pela polícia para demarcar operações de trânsito? Sim, são cones. O que mais vem à sua lembrança? Veja as imagens de cones a seguir e os Elementos dos Cones:

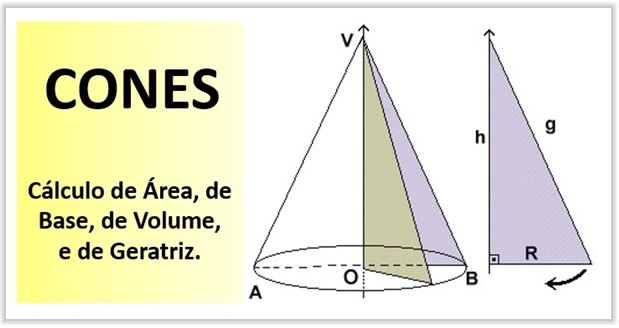
Veja os Elementos do Cone: Vértice, Eixo, Geratriz, Altura
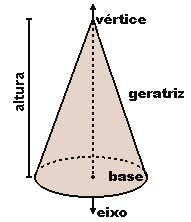
- Base: A base do cone é a região plana contida no interior da curva, inclusive a própria curva.
- Vértice: O vértice do cone é o ponto V.
- Eixo: Quando a base do cone é uma região que possui centro, o eixo é o segmento de reta que passa pelo vértice P e pelo centro da base.
- Geratriz: Qualquer segmento que tenha uma extremidade no vértice do cone e a outra na curva que envolve a base.
- Altura: Distância do vértice do cone ao plano da base.

- Superfície lateral: A superfície lateral do cone é a reunião de todos os segmentos de reta que tem uma extremidade em P e a outra na curva que envolve a base.
- Superfície do cone: A superfície do cone é a reunião da superfície lateral com a base do cone que é o círculo.
- Seção meridiana: A seção meridiana de um cone é uma região triangular obtida pela interseção do cone com um plano que contem o eixo do mesmo.

A Classificação dos Cones Retos e dos Clones Oblíquos
Quando observamos a posição relativa do eixo em relação à base, os cones podem ser classificados como retos ou oblíquos. Um cone é dito reto quando o eixo é perpendicular ao plano da base e é oblíquo quando não é um cone reto. Ao lado apresentamos um cone oblíquo.
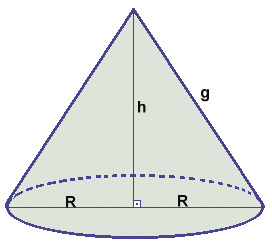
Cone reto
Cone oblíquo
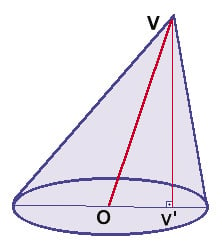
Observações sobre um cone circular reto
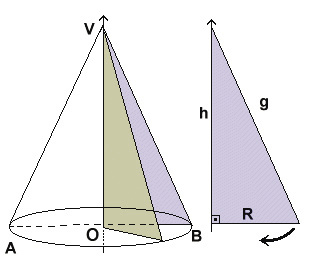
- Um cone circular reto é chamado cone de revolução por ser obtido pela rotação (revolução) de um triângulo retângulo em torno de um de seus catetos
- A seção meridiana do cone circular reto é a interseção do cone com um plano que contém o eixo do cone.
No caso acima, a seção meridiana é a região triangular limitada pelo triângulo isósceles VAB.
Cone equilátero é aquele onde a geratriz igual ao diâmetro da base (g = 2R). A secção meridiana é um triângulo equilátero.
Em um cone circular reto, todas as geratrizes são congruentes entre si. Se g é a medida de cada geratriz, então, pelo Teorema de Pitágoras, temos:
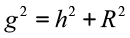
Fórmulas para os cálculos envolvendo os Cones
Área da base: 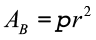
Área lateral: 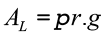
Área total: 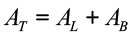
Volume: 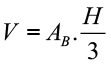
Aula Gratuita sobre cone e geometria espacial:
Desafios para você resolver e compartilhar
Questão 01
Dois amigos, Antônio e José, foram tomar chope num lugar onde existem dois tipos diferentes de copos, conforme as figuras abaixo.
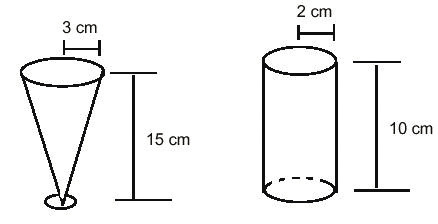
Antônio escolheu o copo cônico, José escolheu o cilíndrico e cada um tomou 10 copos de chope.
Considerando π = 3,14 , pode-se afirmar que:
a) Antônio tomou mais de 2 litros de chope.
b) Antônio e José tomaram quantidades iguais de chope.
c) Antônio tomou 1 / 2 litro de chope a mais que José.
d) Antônio e José, juntos, tomaram mais de 2 litros de chope.
Dica 1 – Relembre sobre o conceito e os tipos de Cilindros nesta aula preparatória para a prova de Matemática Enem. Estude conosco e fique preparado para o Exame! – https://blogdoenem.com.br/cilindro-matematica-enem/
Questão 02
Uma caixa d`água, com capacidade de 81 m3 de volume, tem a forma de um cone circular reto invertido, conforme a figura. Se o nível da água na caixa corresponde a 1/3 da altura do cone, o volume de água existente, em litros, é:
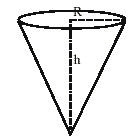
a) 10.000
b) 20.000
c) 30.000
d) 40.000
e) 50.000
Dica 2 – Se você ainda não sabe o que é um poliedro, e que as Pirâmides são poliedros, então preparamos esta aula para você gabaritar na prova de Matemática Enem – https://blogdoenem.com.br/piramide-matematica-enem/
Questão 03
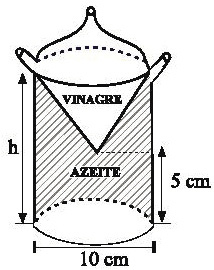
A figura representa um galheteiro para a colocação de azeite e vinagre em compartimentos diferentes, sendo um cone no interior de um cilindro. Considerando h como a altura máxima de líquido que galheteiro comporta e a razão entre a capacidade total azeite e vinagre igual a 5, o valor de h é:
a) 7 cm.
b) 8 cm.
c) 10 cm.
d) 12 cm.
e) 15 cm.
Dica 3 – Nesta aula de revisão para a prova de Matemática Enem você vai estudar a classificação, as nomenclaturas e os cálculos de volume e áreas dos Prismas – https://blogdoenem.com.br/estudo-dos-prismas-matematica-enem/
Questão 04
Uma jarra cilíndrica, com 20cm de profundidade e 10cm de diâmetro, está completamente cheia de suco de laranja. Este suco deverá ser servido em taças cônicas com 12cm de profundidade e 4cm de diâmetro. O número mínimo de taças necessária, para esvaziar completamente a jarra, será de:
a) 26
b) 30
c) 11
d) 16
e) 32
Questão 05
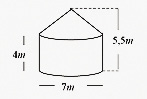
A figura abaixo representa um galpão de base circular e suas medidas estão nela representadas. Quan os metros quadrados de telhado, aproximadamente, foram gastos para cobrir esse galpão?
a) 42m2
b) 41m2
c) 42,5m2
d) 41,5m2
e) 45,5m2
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!


