Aprenda mais sobre Trigonometria aqui no Blog do ENEM com mais de 300 mil exercícios da Khan Academy e o aplicativo Geogebra. Depois dessa aula, você estará pronto para enfrentar o ENEM ou os Vestibulares mais concorridos.
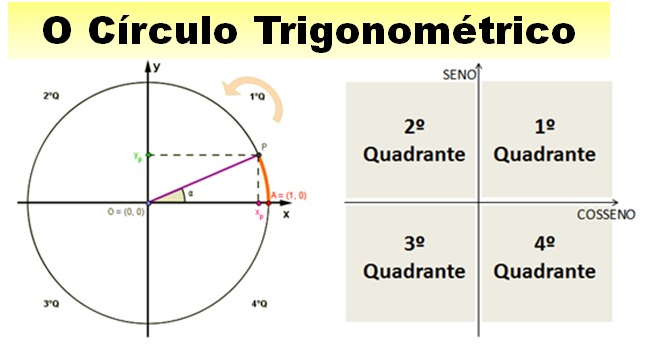
Introdução ao Círculo Trigonométrico: Ele consiste em um círculo de raio unitário (igual a um), cujo eixo vertical denomina-se de SENO e o eixo horizontal de COSSENO. Domine o Círculo para que ele vire um forte aliado para você resolver as questões de trigonometria.
Você entendeu ‘de primeira’, ou teve que parar para pensar? É normal ter que refletir um pouco para recuperar este conteúdo. Se você já estudou Seno, Cosseno e Tangente, então pode compreender o processo para escrever e ler as principais razões trigonométricas de um triângulo retângulo, certo? Vamos lá, então, ao Círculo Trigonométrico.
Mas, se você está em dúvida, ‘volte uma casa’ e clique no link a seguir e faça um novo estudo, veja mais de uma vez os vídeos indicados e refaça os exercícios da plataforma do Khan Academy e do blog do ENEM.
O Círculo Trigonométrico
Aprenda agora na aula bem didática do professor Lucas Borguesan, do canal do Curso Enem Gratuito, para você dominar de maneira prática os segredos do Círculo Trigonométrico:
As dicas sobre o Círculo Trigonométrico:
- O ciclo trigonométrico é um círculo de raio 1. Ou seja, do seu cento até a borda, a medida é 1.
- Assim, podemos definir todos os valores de seno e cosseno que existem, uma vez que o círculo trigonométrico compreende todos os ângulos.
- Na trigonometria, seno e cosseno são chamados de razões trigonométricas.
- Para medir o valor do seno, é comum usar o eixo vertical do círculo trigonométrico. Desta forma, o eixo vertical do ciclo trigonométrico é chamado eixo dos senos.
- Por outro lado, podemos encontrar o valor do cosseno no eixo horizontal, de maneira que este é chamado de eixo dos cossenos.
- Veja novamente o resumo acima, para você dominar e mandar bem no Enem com este forte aliado.
Veja aqui uma revisão completa de Seno, Cosseno, e Tangente.
O Círculo trigonométrico é seu forte aliado
Ao trabalharmos em trigonometria somente com os ângulos notáveis, estamos restringindo muito o campo de ação desse ramo da Matemática. Sendo assim, é importante termos consciência de que outros ângulos maiores do que 90º possuem seus respectivos valores de SENO, COSSENO e TANGENTE.
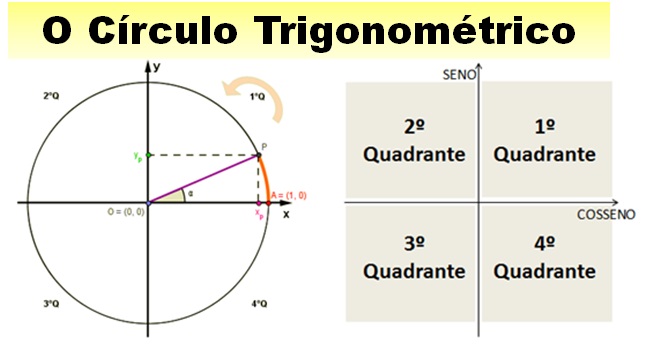
Pensando em uma forma de aglutinar todo esse raciocínio incluindo as relações trigonométricas para ângulos acima de 90° é que foi desenvolvido o círculo trigonométrico. Veja a ilustração acima e observe, antes de ler a definição de Círculo Trigonométrico.
Definição do Círculo Trigonométrico:
O Círculo Trigonométrico consiste em um círculo de raio unitário (igual a um), cujo eixo vertical denomina-se de SENO e o eixo horizontal de COSSENO. Para entender melhor esse processo, acesse o applet a seguir desenvolvido através do Geogebra: http://tube.geogebra.org/student/mdaP7mPvF.
Os quadrantes do Círculo Trigonométrico
O interessante do círculo trigonométrico é notar a relação entre os valores de SENO e COSSENO em cada um dos quadrantes. Por exemplo, podemos notar que um ângulo do 1º quadrante terá o mesmo triângulo descrito no 2º quadrante de duas formas:
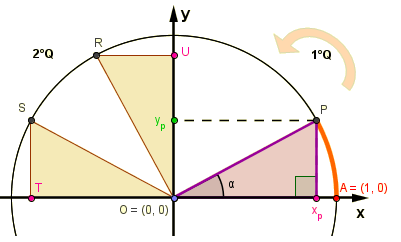
Repare que os triângulos POX e ROU são congruentes, assim como os triângulos POX e SOT. Com isso, podemos identificar outras importantes relações trigonométricas:
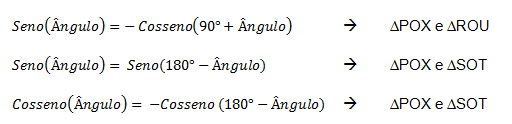
Use o applet acima novamente para identificar todas essas relações ao longo do restante do círculo trigonométrico. E aproveite o vídeo a seguir para ampliar mais a sua capacidade de leitura deste importante instrumento para o ENEM ou Vestibulares.
Veja o App Geogebra
Agora, vamos ampliar um pouco mais a sua capacidade de trabalhar com as razões trigonométricas. Você já chegou a acessar o applet feito com o Geogebra? Lá na versão de estudante, eu lancei dois questionamentos que você poderá conferir aqui abaixo.
O primeiro questionamento tem a intenção de fazer você manipular os controles deslizantes do Geogebra e verificar o que acontecia com o triângulo e todos os valores a ele associados.
Mas em especial, o segundo questionamento tem por objetivo levar você a perceber que para alguns pares específicos de ângulos os valores de senos ficavam iguais. Em especial, dois deles nos ajudarão muito: B = 30° e C = 60°.
Veja as figuras abaixo nas duas situações possíveis de construir com o applet:
Na primeira situação podemos notar que o valor de B = 60° possui aproximadamente a mesma razão do valor de C = 60° da segunda situação. Veja:
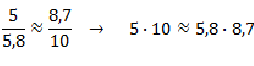
Além disso, podemos notar também que o valor de B = 30° na primeira situação é exatamente igual ao valor de C = 30° na segunda situação. Veja:
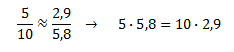
Isso ocorreu, pois os triângulos de cada situação são semelhantes entre si. Lembra-se desse conceito de semelhança?
Dica 1: Revise um pouco antes de continuar aqui no blog do ENEM em https://blogdoenem.com.br/semelhanca-entre-triangulos-matematica-enem/
Ou seja, quando atribuíamos ao ângulo B na primeira situação o valor dele, estávamos ao mesmo tempo descrevendo o seno do ângulo C e, sem você se dar conta, o cosseno do ângulo B. Reveja a tabela da aula anterior de Seno, Cosseno e Tangente aqui no blog do ENEM. https://blogdoenem.com.br/seno-cosseno-tangente-enem-vestibular/
Seno (30º) = Cosseno (60°) = ½
Isso ocorreu, pois os ângulos B = 30° e C = 60° são complementares.
Dica 2: Reveja a aula de Ângulos e suas classificações – Matemática ENEM em https://blogdoenem.com.br/angulos-matematica-enem/.
Agora que você já está habituado a reconhecer os senos e cossenos de ângulos complementares, vamos definir uma fórmula geral para essa situação.
seno(ângulo) = cosseno(90º-Ângulo)
Desafios para dominar seu forte aliado
1 – (VUNESP) Uma pessoa, no nível do solo, observa o ponto mais alto de uma torre vertical, à sua frente, sob o ângulo de 30º. Aproximando-se 40 metros da torre, ela passa a ver esse ponto sob o ângulo de 45º. A altura aproximada da torre, em metros, é:
- a) 44,7 b) 48,8 c) 54,6 d) 60,0 e) 65,3
Dica: veja o desenho desta situação abaixo
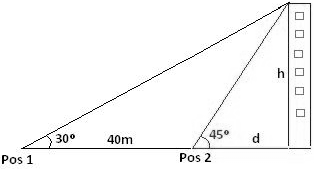
2 – (UFRS) Um barco parte de A para atravessar o rio. A direção de seu deslocamento forma um ângulo de 120° com a margem do rio. Sendo a largura do rio 60m, a distância, em metros, percorrida pelo barco foi de:
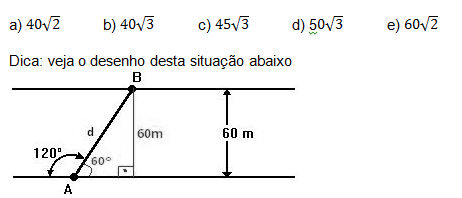
Resolva mais exercícios de Trigonometria com a Khan Academy e vá confiante para a prova do ENEM ou Vestibular:
Gabarito: 1) C ; 2) B
Autoria de Davi Rissetti, o seu forte aliado professor de matemática.
Este post é resultado da parceria da Fundação Lemann com o Blog do Enem – www.fundacaolemann.org.br