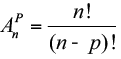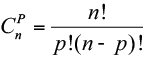Veja agora o conceito e os exemplos de aplicação prática sobre dois tipos de combinação: a simples e a com repetição de elementos. Veja os fundamentos da Análise Combinatória.
Aprender a resolver questões de Análise Combinatória Simples, ou com Repetição de Elementos faz parte dos conteúdos classicos da Matemática. E cai direto no Enem, no Encceja e nos vestibulares. Para quem vai fazer concursos de nível médio também conta muitos pontos.
Então, a hora é de se ligar para aprender e mandar bem. Os fundamentos para você dominar esta área estão na Aula de Introdução ao tema de Permutação com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito. Em seguida você revisa também a Análise Combinatória, para usar e gabaritar nas provas.
Resumo de Permutação com Repetição de Elementos
A permutação é uma das formas de agrupamentos ordenados dentro da chamada análise combinatória, onde o número de elementos (n) do agrupamento é igual ao número de elementos disponíveis.
O Princípio Fundamental da Contagem:
- “Se uma decisão d1 pode ser tomada de x maneiras diferentes e se, uma vez tomada a decisão d1, a decisão d2 puder ser tomada de y maneiras diferentes, então o número de maneiras de se tomarem as decisões d1 e d2 é dado pelo produto x . y.”
- Observação importante: O princípio multiplicativo pode ser generalizado para mais de duas decisões.

Veja neste Exemplo:
- Numa sala existem 3 garotas (Adriana, Beatriz e Cleide) e 2 rapazes (Rodrigo e Sandro). Quantos casais diferentes podemos formar com essas 5 pessoas?
- Resolução: – Para formarmos um casal precisamos agrupar 1 homem e 1 mulher, isto é, precisamos tomar uma decisão d1 que consiste na escolha de um homem e tomar uma decisão d2, que consiste na escolha de uma mulher.
- • A decisão d1 pode ser tomada de 2 maneiras diferentes (existem 2 homens);
• A decisão d2 pode ser tomada de 3 maneiras diferentes (existem 3 mulheres). - Logo, o número total de casais é 2.3 = 6.
O Cálculo Fatorial
Definição de Fatorial: Seja n um número natural maior que 1. O fatorial de n, indicado por n!, é definido como o produto dos n números naturais consecutivos de 1 até n, isto é: n! = n.(n – 1) . (n – 2) . … .3.2.1 onde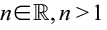 Observação importante sobre Fatorial: convencionou-se que 0! = 1 e que 1! = 1
Observação importante sobre Fatorial: convencionou-se que 0! = 1 e que 1! = 1
Exemplos para você relembrar Fatorial:
- Exemplo A – Veja o ‘Cinco Fatorial’
- 5! = 5.4.3.2.1
- Exemplo B – Veja o ‘Oito Fatorial’
- 8! = 8.7.6.5.4.3.2.1
Esse conceito de fatorial aparece em várias fórmulas na análise combinatória, como as apresentadas a seguir.
Agrupamentos por Arranjo simples
- Definição: “Seja E um conjunto com n elementos, isto é, E = {a1,a2, a3, …, an} . Chamamos de arranjos simples dos n elementos de E tomados P a P (1≤ p ≤ n) a qualquer sequência formada por P elementos distintos de E.”
- Símbolo: An . P ou APn.
- Fórmula:

Combinação simples
- Definição: “Seja E um conjunto com n elementos, isto é, E = {a1,a2, a3, …, an} . Chamamos de arranjos simples dos n elementos de E tomados P a P (1≤ p ≤ n) a qualquer subconjunto de E formada por P elementos.”
- Símbolo: Cn . P ou CPn.
- Fórmula:

Obs.: Veja que a diferença entre arranjo e combinação está na ordem dos elementos. Como arranjo é uma sequência, a mudança de ordem gera um novo grupo, enquanto na combinação isto não ocorre.
Considere o seguinte exemplo
- Com os elementos do conjunto {1,2,3,4,5,6},
- a) Quantas senhas de 3 algarismos distintos podemos formar?
- b) Quantos subconjuntos de 3 elementos distintos podemos formar?
Veja a Resolução:
a) Veja que a senha 123 é diferente de 321. Neste caso, como a variação da ordem gera uma nova senha, cada um desses grupos é considerado um arranjo de 6 elementos tomados 3 a 3. O total é dado por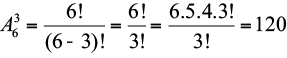
b) O subconjunto {1,2,3} é o mesmo que {3,2,1}. Neste caso, como a variação da ordem dos elementos não gera um novo agrupamento, estamos diante de um problema de combinação. O total de subconjuntos é dado por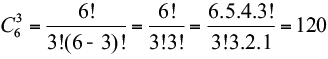
Resumo de Análise Combinatória
Confira com o professor Vinny, do Curso Enem Gratuito, uma outra maneira de aprender a resolver Análise Combinatória Simples ou com Repetição de Elementos:
Viu como é simples de aprender com o professor Vinny?
Aprenda Permutação simples
Este é um conceito muito simples, pois permutação é um caso particular de arranjo. Além disso, o termo permutação é bastante sugestivo e, neste sentido, o que irá ser feito é, essencialmente, permutar as posições de elementos de um conjunto dado.
- Definição: “Seja E um conjunto com n elementos, isto é, E = {a1,a2, a3, …, an} . Chamamos de permutação simples dos n elementos de E a qualquer sequência formada pelos n elementos distintos de E.”
- Símbolo: Pn.
- Fórmula: Pn = n!
Veja neste exemplo bem simples: – Quantos são os anagramas da palavra AMOR?
Acompanhe a Resolução: > Anagramas da palavra amor são todas as palavras, com ou sem significado, que criamos usando todas as letras da palavra dada. Alguns deles são ROMA, ROAM, MORA, AMOR, MROA, etc.
A Resposta: Veja que estamos simplesmente permutando todas as 4 letras. Assim, o total de anagramas é dado por P4 = 4! = 24
Novo Desafio: > E se a palavra fosse BATATA?
Neste caso tem-se uma Permutação com Repetição, e a fórmula é esta: 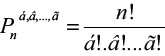 (n objetos, onde um deles se repete á vezes, outro às vezes, e assim por diante).
(n objetos, onde um deles se repete á vezes, outro às vezes, e assim por diante).
Calculando então o total de anagramas da palavra BATATA, temos 6 letras, com A repetindo 3 vezes e T duas vezes.
Aula Gratuita sobre Análise Combinatória
Agora, para você completar a revisão de Análise Combinatória, assista esta aula em vídeo, e, logo em seguida, resolva os exercícios ao final da página.
Dica 3 – Você já estudou sobre juros simples e juros compostos? Revise tudo sobre cálculo de porcentagem e juros em mais uma aula de Matemática Enem – https://blogdoenem.com.br/porcentagem-juros-simples-e-compostos-matematica-enem/
Exercícios de aplicação – Análise Combinatória
Desafio 01
Com os números do conjunto {1, 2, 3, 4, 5, 6} quantas senhas
a) de 3 letras podemos formar?
b) de 3 letras distintas podemos formar?
Exercício 02
Com as letras A, B, C, D, E quantas senhas de 3 letras distintas podemos formar?
Exercício 03
Com as frutas A, B, C, D, E quantas vitaminas de 3 frutas podemos formar?
Exercício 04
Quantos anagramas da palavra SONHAR começam e terminam por vogal?
Exercício 05
(ENEM, 2ª aplicação, 2010) Considere que um professor de arqueologia tenha obtido recursos para visitar 5 museus, sendo 3 deles no Brasil e 2 fora do país. Ele decidiu restringir sua escolha aos museus nacionais e internacionais relacionados na tabela a seguir.
|
Museus nacionais |
Museus internacionais |
|
Masp – São Paulo |
Louvre – Paris |
|
MAM – São Paulo |
Prado – Madri |
|
Ipiranga – São Paulo |
British Museum – Londres |
|
Imperial – Petrópolis |
Metropolitan – Nova York |
De acordo com os recursos obtidos, de quantas maneiras diferentes esse professor pode escolher os 5 museus para visitar?
a) 6
b) 8
c) 20
d) 24
e) 36
Desafios
Questão 01
(ENEM, 2009) Doze times se inscreveram em um torneio de futebol amador. O jogo de abertura do torneio foi escolhido da seguinte forma: primeiro foram sorteados 4 times para compor o Grupo A. Em seguida, entre os times do Grupo A, foram sorteados 2 times para realizar o jogo de abertura do torneio, sendo que o primeiro deles jogaria em seu próprio campo, e o segundo seria o time visitante.
A quantidade total de escolhas possíveis para o Grupo A e a quantidade total de escolhas dos times do jogo de abertura podem ser calculadas através de:
a) Uma combinação e um arranjo, respectivamente.
b) Um arranjo e uma combinação, respectivamente.
c) Um arranjo e uma permutação, respectivamente.
d) Duas combinações.
e) Dois arranjos.
Questão 02
(ENEM, 2004) No Nordeste brasileiro é comum encontrarmos peças de artesanato constituídas por garrafas preenchidas com areia de diferentes cores, formando desenhos. Um artesão deseja fazer peças com areia de cores cinza, azul, verde e amarela, mantendo o mesmo desenho, mas variando as cores da paisagem (casa, palmeira e fundo), conforme a figura.

O fundo pode ser representado nas cores azul ou cinza; a casa, nas cores azul, verde ou amarela; e a palmeira, nas cores cinza ou verde. Se o fundo não pode ter a mesma cor nem da casa nem da palmeira, por uma questão de contraste, então o número de variações que podem ser obtidas para a paisagem é:
a) 6
b) 7
c) 8
d) 9
e) 10
Questão 03
(ENEM, 2005) A escrita Braile para cegos é um sistema de símbolos no qual cada caractere é um conjunto de 6 pontos dispostos em forma retangular, dos quais pelo menos um se destaca em relação aos demais.
Por exemplo, a letra A é representada por:

O número total de caracteres que podem ser representados no sistema Braile é:
a) 12
b) 31
c) 36
d) 63
e) 720
Questão 04
(ENEM, 2007) Estima-se que haja no Acre 209 espécies de mamíferos, distribuídas conforme a tabela a seguir:
Deseja-se realizar um estudo comparativo entre três dessas espécies de mamíferos – uma do grupo cetáceos, outra do grupo primatas e a terceira do grupo roedores.
O número de conjuntos distintos que podem ser formados com essas espécies para esse estudo é igual a:
a) 1.320
b) 2.090
c) 5.845
d) 6.600
e) 7.245
Questão 05
(ENEM, 2011) O setor de Recursos Humanos de uma empresa vai realizar uma entrevista com 120 candidatos a uma vaga de contador. Por sorteio, eles pretendem atribuir a cada candidato um número, colocar a lista de números em ordem numérica crescente e usá-la para convocar os interessados. Acontece que, por um defeito do computador, foram gerados números com 5 algarismos distintos e em nenhum deles apareceram dígitos pares.
Em razão disso, a ordem de chamada do candidato que tiver recebido o número 75.913 é
a) 24
b) 31
c) 32
d) 88
e) 89
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
Veja agora outra explicação para Combinação:
Combinações são agrupamentos de k elementos, de forma que os k elementos sejam distintos entre si apenas pela espécie. A posição dos elementos não importa e não os distingue.