Quem acerta uma questão de Matrizes no Enem arranca na frente da concorrência. Veja agora as definições, os tipos de matrizes, e aprenda a fazer o Cálculo do Determinante. Não se assuste com os nomes. O professor Lucas Borguezan vai traduzir tudo de um jeito que você entende, aprende, e gabarita na prova de matemática. Vem!
Determinante é um tipo de matriz, mas essa deverá ter o mesmo número de linhas e o mesmo número de colunas, ou seja, uma matriz quadrada. Nele não aplicamos as quatro operações, mas há outras propriedades, como achar o valor numérico dos determinantes.
Você compreendeu assim “de primeira”, ou deu aquela engasgadinha, e precida revisar um pouco para mandar bem? Então, não tem problema. Primeiro veja o resumo de Matrizes, e logo em seguida vamos ao Determinante.
O que são as MATRIZES?
O professor Lucas Borguezan, do canal do Curso Enem Gratuito, preparou um resumo especial para você tirar as principais dúvidas sobre as Matrizes. Confira agora:
- O método de resolução para equações matriciais é o mesmo utilizado para equações envolvendo números reais: queremos usar as operações básicas com o objetivo de isolar a incógnita.
- Entretanto, o trabalho com matrizes envolve algumas regras específicas que vamos aprender nessa aula.
Nesta aula você vai conferir o determinante de uma matriz de ordem 2 e ordem 3 e suas propriedades. Faça parte desta aula e arrase em matemática no Enem!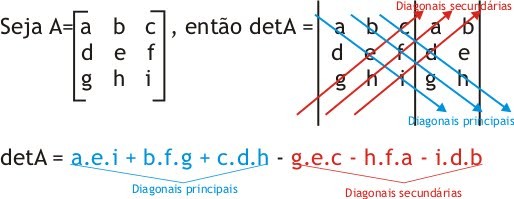
O Determinante
- Podemos calcular o determinante de qualquer matriz desde que essa seja quadrada, ou seja, que a matriz tenha o mesmo número de linhas e de colunas (seja uma matriz de ordem n x n).
- Podemos dizer que determinante de uma matriz quadrada é o seu valor numérico.
- Os elementos de uma matriz podem ser colocados entre parênteses, colchetes ou entre duas barras duplas; e os elementos dos determinantes são colocados entre duas barras.
-
Veja como fazer o cálculo dos Determinantes:
As dicas do professor Lucas
- Para determinar o número de soluções de um sistema de matrizes é preciso utilizar a matriz dos coeficientes.
- Para isso, precisamos calcular o determinante da matriz dos coeficientes e analisar seu resultado.
- Mais precisamente: quando o determinante da matriz dos coeficientes for diferente de 0 sabemos que o sistema em questão possui uma única solução.
- Ou seja, que o sistema é possível e determinado.
- Em contrapartida, quando o determinante da matriz dos coeficientes de um sistema for igual a 0, sabemos que é possível e indeterminado (infinitas soluções) ou que ele é impossível (nenhuma solução)
- Nesta aula acima, o professor Lucas te ensina a fazer o cálculo de determinante com mais detalhes.
Determinante na Matriz de Ordem 1
Quando uma matriz possui apenas um elemento ou possui apenas uma linha e uma coluna, dizemos que essa matriz é de ordem 1. Veja alguns exemplos:

Conseguiu compreender? Se precisar, volte aos vídeos com o professor Lucas Borguezan, que eles te ajudam no aprendizado essencial de Matrizes e Determinantes.
Determinante na Matriz de Ordem 2
A – Determinante de uma matriz quadrada de 2ª Ordem
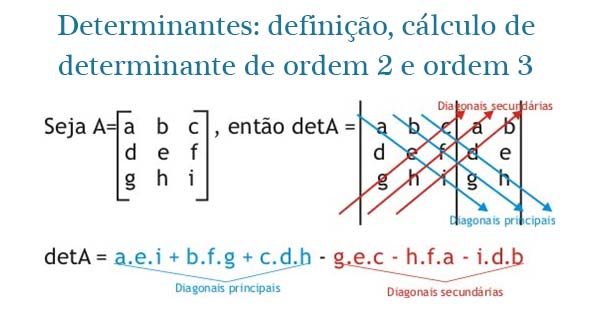
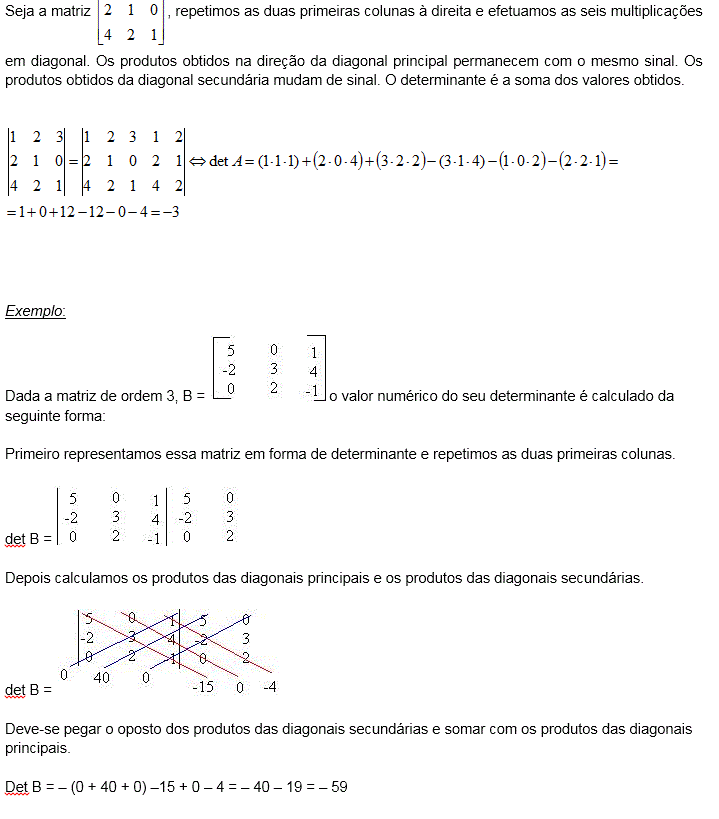
Regra de Sarrus: regra prática para calcular determinantes de ordem 3
Você está conseguindo acompanhar e aprender o raciocínio e o modo de resolver os problemas para o Cálculo do Determinante nas Matrizes? É preciso um pouco de calma e persistência.
Quer ver mais? Confira o Teorema de Laplace, e a Regra de Chió.
Exercícios sobre o cálculo do Determinante