Olá pessoal, hoje vamos aprender sobre o conceito de intervalo. Para isso, que tal assistir a aula de conjuntos antes para entenderem esse assunto direitinho para o Enem 2013? Vamos lá.
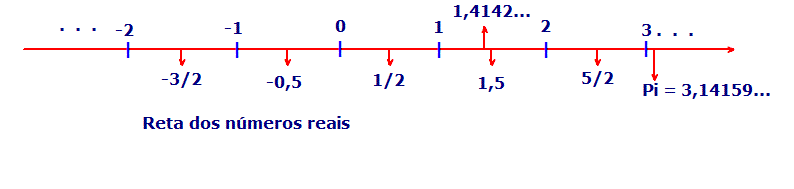
Antes de começarmos nossa aula sobre com intervalos para o Enem 2o13, vamos relembrar que todos os números estão representados numa reta, na qual eles estão dispostos de maneira que os menores sempre estão à esquerda, ou seja, é uma reta crescente da esquerda pra direita. Chamamos essa reta de reta Real ou reta dos Números Reais. Qualquer número que vocês possam imaginar está contido nessa reta.
Suponha agora que não queremos falar de toda a reta e sim de um intervalo específico. Por exemplo, o intervalo que chamaremos de A.
O intervalo A vai do -2 até o +2, porém não queremos que +2 pertença ao nosso intervalo, ou seja, queremos que o limite superior do intervalo seja o maior número menor que +2. Vamos agora dar as diferentes notações do intervalo A para seu Enem 2013:
Dica do Blog do Enem: Veja aqui o que mais cai em todas as provas – https://blogdoenem.com.br/category/cainaprova/
Notação geométrica:
A= 
O que fizemos foi pintar de verde o intervalo desejado. No extremo esquerdo, quando a bolinha é fechada, queremos dizer que -2 pertence ao intervalo A. Já no caso do extremo direito, +2 não pertence a A, pois não queremos isso. Portanto, o limite do intervalo é uma bolinha aberta. Assim, para seu Enem 2013, você deve notar que, quando o número faz parte, a bolinha é fechada; e quando o número não faz parte do conjunto ou do intervalo, a bolinha é aberta.
Notação de conjuntos para o Enem 2013: 
, onde “x” quer dizer: todos os “x” tal que. Como assim? A é o conjunto de todos os “x”, tal que -2 é menor ou igual que x e, ao mesmo tempo, x tem que ser menor que 2. Note que menor ou igual significa que x pode ser igual a -2; e menor significa que x nunca pode ser 2, mas pode ser um número muito próximo de 2, por exemplo 1,9999999…
Notação Simbólica para o Enem 2013: O nosso intervalo pode ser representado da seguinte maneira: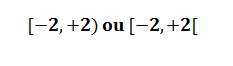
Vamos entender a notação acima para o Enem 2013. Quando o extremo de um intervalo está contido no intervalo, representamos ele por colchetes, que é o caso do -2. Ele é extremo do nosso intervalo A e ao mesmo tempo está contido em A. Já o caso do +2 é diferente: ele é extremo de A, porém não faz parte do intervalo. Assim, tem um parênteses ao seu lado.
Regra para seu Enem 2013: colchetes virados para o lado externo do intervalo tem o mesmo sentido de parênteses, ou seja, intervalo aberto.
Assim, em nossa notação simbólica, dizemos que o intervalo A é aberto a direita e fechado a esquerda.
Exemplos:
a) Notação geométrica: 
b) Notação de Conjunto: 
c) Notação Simbólica: 
O intervalo acima é dito fechado a esquerda e a direita, pois seus dois extremos estão contidos no conjunto.
Agora que já sabemos mais sobre intervalos, vamos assistir uma aula do professor Nerckie, do canal Vestibulandia.com, que ensina a fazer a união e a intersecção dos intervalos. Vamos lá?
Gostaram, galera? Para vocês se darem muito bem no Enem 2013, podem assistir a parte final dessa aula aqui.
RESPOSTAS:
1a) intervalo fechado entre 6 e 10, ou seja, bolinha fechada nos dois extremos.
1b) intervalo aberto em -1 e fechado em 5, ou seja bolinha aberta à esquerda e fechado à direita.
Esclarecemos que quando um intervalo tem extremos em o extremo correspondente é sempre aberto.
Subtração de intervalos tem o mesmo sentido de subtração de conjuntos, ou seja, A-B significa, tudo de A e nada de B.
Confira o Simulado Enem 2013 – Clique AQUI.
Confira Como se preparar para o Enem 2013 – Clique AQUI.
Agora que você já sabe tudo sobre o Enem 2013, que tal conhecer nossa rede de blogs?
