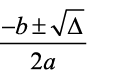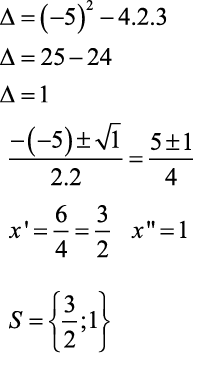Nesta aula de Matemática Enem vamos revisar sobre Estudo do Delta, Equação Polinomial do 2º grau e como resolver este tipo de equação. Vamos lá? Cai no Enem e nos vestibulares
Você lembra como é uma equação de segundo grau? Vamos relembrar?
Denomina-se equação de segundo grau qualquer sentença matemática que possa ser reduzida à forma: ax² +bx +c = 0, com a ≠0
- Onde x é a incógnita e a, b e c são números reais, com a ≠ 0. a, b e c são coeficientes da equação. Observe que o maior índice da incógnita na equação é igual a dois e é isto que a define como sendo uma equação do segundo grau.
- Veja nestes Exemplos:
- a) 2x² -5x +3 = 0
- b) -x² +9 = 0

Dica 1 – O que mais cai em Matemática nos Vestibulares e no Enem? Veja aqui as melhores dicas: https://blogdoenem.com.br/category/cainaprova/matematica/
Mas como solucionar este tipo de equação? Calma! O Blog do Enem não te deixa na mão! Vamos explicar tudo direitinho pra você. Preste atenção!
Dentre as várias maneiras de solucionar uma equação de segundo grau, temos como a mais comum e mais utilizada as fórmulas de delta e Bhaskara. Confira:
- Primeiramente você deverá calcular o valor do Delta (∆), através da equação:
- ∆ = b² – 4ac
- Onde a, b e c são os coeficientes da equação.
- Depois de calculado o Delta, você o substituirá na equação abaixo, para obter os valores das raízes da equação, ou seja, os valores do x.

Veja o exemplo para ficar mais fácil:
Encontre a solução da equação x² -5x +3 =0
- Para solucionar x² -5x +3 = 0 vamos aos seguints passos:
- Temos que os coeficientes da equação são: a=2, b=-5 e c=3
- Assim:

Aula Gratuita: prepare-se para o Enem com essa super aula de Equação do segundo grau
Muito boa a didática do professor Sérgio Sarkis. Têm mais aulas de matemática com ele no canal de aulas do Curso Enem Gratuito.
Dica 2 – Pronto para gabaritar na prova de matemática do Enem? Faça uma revisão com esta aula sobre Equações Polinomiais do 1º grau – https://blogdoenem.com.br/funcao-polinomial-matematica/
Agora vamos fazer um estudo sobre o valor do Delta?
O delta nos criará três situações distintas na resolução de uma equação, vamos a elas:
- Para ∆ < 0, ou seja, para valores de Delta menores do que Zero: Não teremos raízes Reais.
- Para ∆ = 0 , ou seja, valores de Delta iguais à zero: Teremos duas raízes Reais e Iguais.
- Para ∆ > 0, Delta maior do que zero: Teremos duas raízes Reais e Distintas.
Resumo Gratuito: Soma e Produto nas Equações do 2º Grau
Confira uma abordagem diferente para resolver os problemas com Equações do 2º Grau com o método de Soma e Produto. Já vimos que as equações de segundo grau são expressões algébricas de grau 2, igualadas a zero, que podem ser resolvidas por meio da fórmula de Bháskara. Mas, têm outros caminhos:
A técnica da soma e do produto facilita na resolução de equações do segundo grau. Nessa parte do vídeo, o professor explica essa técnica. Vale lembrar que quando o delta for negativo, não haverá raízes da equação e, portanto, não há como resolver todas as equações por soma e produto.
Soma e Produto das Raízes
Existe ainda outra forma de encontrar as raízes da equação, que é através da “soma e produto”, vamos vê-las?
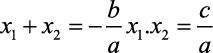
Entendeu? Vamos ver como é feito:
Observe a seguinte equação:
x2 – 5x + 6 = 0
Você poderia responder: Quais são os dois números que somados totalizam 5 e que multiplicados resultam em 6?
É muito provável que mentalmente você tenha identificado rapidamente que os dois números procurados são 2 e 3, pois 2 + 3 = 5 e 2 . 3 = 6.
Mas de onde surgiu a questão “Quais são os dois números que somados totalizam 5 e que multiplicados resultam em 6?”
É isso mesmo! Utilizando a equação mostra acima, onde a soma das raízes da equação é igual ao resultado da divisão do coeficiente B pelo a com o sinal negativo na frente da equação e a multiplicação dessas mesmas raízes é igual a divisão entre os coeficientes a e b da equação de segundo grau.
Dica 4 – Relembre outros assuntos de matemática acessando o nosso blog www.blogdoenem.com.br e gabarite as questões de matemática nas provas dos vestibulares e do Enem.
Veja mais sobre a equação de segundo grau assistindo ao vídeo com as resoluções alternativas para as equações do segundo grau. Cai no Enem e nos vestibulares de todo Brasi!
Exercício sobre equações do Segundo Grau
Você consegue resolver este exercício abaixo ? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
Qual deve ser o valor real de Y para que as equações (2y+1/y+2) e (y+5)/(y+3) sejam iguais?
Resposta:![]()