Relembre tudo sobre Estatística em mais esta aula de revisão para a prova de Matemática Enem. Estude com a gente para o Exame Nacional do Ensino Médio! Confira abaixo aula gratuita com exercícios resolvidos.
Revisão sobre os Fundamentos de Estatística para você lembrar das aulas do Ensino Médio. Vamos lá? Vamos começar pelos conceitos e descrições essenciais para a sua revisão:
1 – Estatística é a ciência que coleta, organiza e interpreta dados coletados entre um grupo que se deseja estudar. Esse grupo pode ser de pessoas, de objetos, de países, etc.
2 – Estatística descritiva Concentra-se mais na coleta, organização, classificação, apresentação e descrição dos dados a serem observados. É a parte da Estatística que estudaremos.
3 – Estatística inferencial Refere-se ao processo de generalização, a partir de resultados particulares. Neste caso há uma margem de incerteza na generalização feita. Mas, nãoo será objeto de nosso estudo nesta aula de revisão básica. Vamos prosseguir com os elementos necessários para os cálculos em Estatistica:
A – População: É o conjunto de pessoas, objetos, etc. que pretendemos estudar. Por exemplo, a população total da cidade de São Paulo.
B – A Amostra: É uma parte da população (um subconjunto). Por exemplo, a população do bairro Vila Madalena, na cidade de São Paulo. É apenas uma parte, um subconjunto da população total da cidade,
C – Variável: É a característica da população que se pretende estudar. Por exemplo, qual a quantidade ou a proporção de pessoas acima de 60 anos que residem no bairro da Vila Madalena. E, depois podemos ainda querer saber qual o percentual deles que são casados ou separados, ou solteiros que nunca se casaram, e se nasceram no Brasil ou em outros países.
- Variável quantitativa: Pode ser mensurável. Pode ser representada através de valores numéricos. Ex: tempo de serviço, peso de crianças.
- Variável qualitativa: Refere-se a um atributo não estruturado numericamente. Ex: estado civil, nacionalidade.
C – Os Dados: São os valores associados às variáveis de pesquisas. Ex: Se a variável em estudo for a idade de crianças, os dados podem ser 3, 5, 1, etc.
D – O Rol: É qualquer lista em ordem crescente (ou decrescente) dos dados coletados associados a uma variável quantitativa.
Por Exemplo: Numa pesquisa sobre idades de 10 alunos de uma sala, os resultados obtidos foram 18,17,18,20,22,21,18,16,19,16.
Um Rol consiste, então, na lista ordenada destas idades: 16,16,17,18,18,18,19,20,21,22.
Distribuição de Frequências
Consiste numa tabela onde os dados são apresentados com as suas respectivas frequências. Essas frequências podem ser absolutas (número de vezes que o dado aparece) ou relativas (percentual de frequência do dado). No exemplo anterior das idades dos 10 alunos de uma sala, a distribuição de frequências é dada pela tabela
|
Idade |
Frequência Absoluta |
Frequência Relativa |
|
16 |
2 |
20% |
|
17 |
1 |
10% |
|
18 |
3 |
30% |
|
19 |
1 |
10% |
|
20 |
1 |
10% |
|
21 |
1 |
10% |
|
22 |
1 |
10% |
|
Total |
10 |
100% |
Medidas de tendência central
É um tipo de medida que tenta representar todo o conjunto de dados. O exemplo mais conhecido é a média aritmética, mas, além dele, veremos outros dois.
Média
A Média (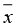 ) ou média aritmética simples de um conjunto x1, x2, …, xn é dada por
) ou média aritmética simples de um conjunto x1, x2, …, xn é dada por
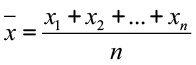
Exemplo:
A média das 10 idades 16,16,17,18,18,18,19,20,21,22 é dada por
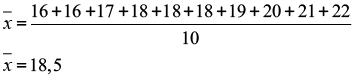
Mediana
Quando os dados estiverem num rol, a mediana (Md) desse conjunto de dados é:
- o valor central, caso a quantidade de dados for ímpar
- a média aritmética dos centrais, caso a quantidade de dados for par
Exemplos – Exercícios Resolvidos.
Exemplo 01 – Para os dados 5,7,7,8,9,15,15, a Mediana será Md = 8, pois é o valor central num universo de sete números.
Exemplo 02 – Para os dados 5,7,7,8,9,15, a Mediana é
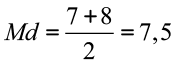 pois há seis números no conjunto.
pois há seis números no conjunto.
Moda
A Moda (Mo) é o valor mais frequente (quando existir) num conjunto de dados.
Exemplos de Moda
- Com os dados 3,3,4,7, a moda é Mo = 3
- Com os dados 3,3,4,4,7, há duas modas: Mo = 3 e Mo = 4. Dizemos que é um conjunto de dados Bimodal.
- Com os dados 3,4,7,9,13,16, não há moda.
Exercício resolvido
Foi feita uma pesquisa com 400 alunos de uma escola sobre suas idades. Os resultados coletados foram organizados na seguinte tabela de distribuição de frequências.
|
Atividade esportiva |
Frequência Absoluta |
Frequência Relativa |
|
13 |
80 |
20% |
|
14 |
120 |
30% |
|
15 |
160 |
40% |
|
16 |
40 |
10% |
|
Total |
400 |
100% |
Calcule a média, a mediana e a moda dessas 400 idades.
Resolução:
- Média: com a tabela de frequências fica muito prático calcular a média
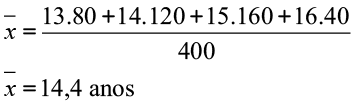
- Mediana: como há uma quantidade par (400) de dados, vamos fazer a média dos valores centrais
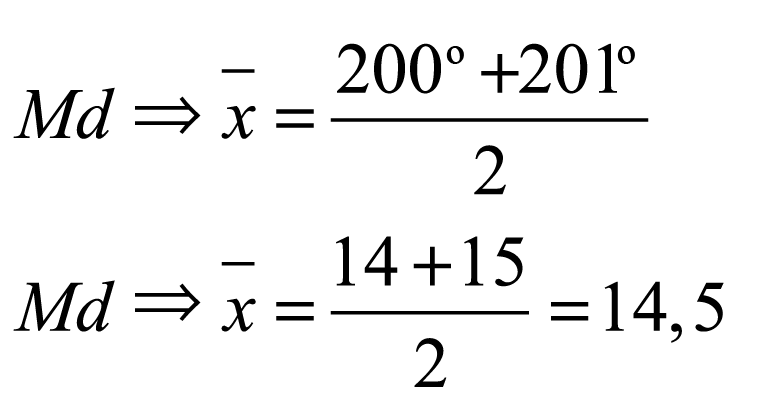
- Moda: Mo=15, pois tem a maior frequência (160 alunos)
Saiba mais sobre Estatística nesta aula do canal Curso Enem Gratuito Quebra tudo no Enem!, disponível no Youtube. Após assistir, revise o que você aprendeu respondendo aos nossos desafios!
Desafios para você resolver e compartilhar a solução
Questão 01
(Enem 2011) O termo agronegócio não se refere apenas à agricultura e à pecuária, pois as atividades ligadas a essa produção incluem fornecedores de equipamentos, serviços para a zona rural, industrialização e comercialização dos produtos.
O gráfico seguinte mostra a participação percentual do agronegócio no PIB brasileiro:
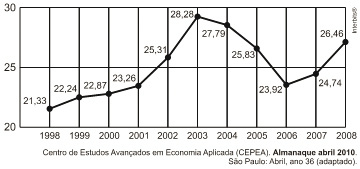
Esse gráfico foi usado em uma palestra na qual o orador ressaltou uma queda da participação do agronegócio no PIB brasileiro e a posterior recuperação dessa participação, em termos percentuais.
Segundo o gráfico, o período de queda ocorreu entre os anos de
a) 1998 e 2001.
b) 2001 e 2003.
c) 2003 e 2006.
d) 2003 e 2007.
e) 2003 e 2008.
Dica 1 – Relembre tudo sobre Probabilidade nesta aula de revisão para a prova de Matemática Enem. Estude com a gente para o Exame Nacional do Ensino Médio! – https://blogdoenem.com.br/probabilidade-matematica-enem/
Questão 02
(Enem 2011) Uma equipe de especialistas do centro meteorológico de uma cidade mediu a temperatura do ambiente, sempre no mesmo horário, durante 15 dias intercalados, a partir do primeiro dia de um mês. Esse tipo de procedimento é frequente, uma vez que os dados coletados servem de referência para estudos e verificação de tendências climáticas ao longo dos meses e anos.
As medições ocorridas nesse período estão indicadas no quadro:
|
Dia do mês |
Temperatura (em ºC) |
|
1 |
15,5 |
|
3 |
14 |
|
5 |
13,5 |
|
7 |
18 |
|
9 |
19,5 |
|
11 |
20 |
|
13 |
13,5 |
|
15 |
13,5 |
|
17 |
18 |
|
19 |
20 |
|
21 |
18,5 |
|
23 |
13,5 |
|
25 |
21,5 |
|
27 |
20 |
|
29 |
16 |
Em relação à temperatura, os valores da média, mediana e moda são, respectivamente, iguais a
a) 17°C, 17°C e 13,5°C
b) 17°C, 18°C e 13,5°C
c) 17°C, 135°C e 18°C
d) 17°C, 18°C e 21,5°C.
e) 17°C, 13,5°C e 21,5°C.
Dica 2 – Que tal revisar sobre Análise Combinatória? Aproveite esta aula e fique preparado para a prova de Matemática Enem. Estude com a gente para o Exame! – https://blogdoenem.com.br/analise-combinatoria-1-matematica-enem/
Questão 03
(Enem 2010) O gráfico apresenta a quantidade de gols marcados pelos artilheiros das Copas do Mundo desde a Copa de 1930 até a de 2006.
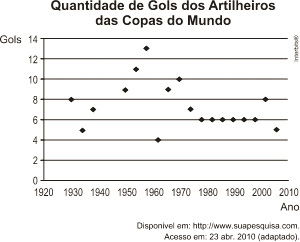
A partir dos dados apresentados, qual a mediana das quantidades de gols marcados pelos artilheiros das Copas do Mundo?
a) 6 gols
b) 6,5 gols
c) 7 gols
d) 7,3 gols
e) 8,5 gols
Dica 3 – Fique preparado para a prova de Matemática Enem com esta segunda aula sobre Análise Combinatória. Revise com a gente e garanta sua nota nas provas do Exame – https://blogdoenem.com.br/analise-combinatoria-2-matematica-enem/
Questão 04
(Enem 2010) O quadro seguinte mostra o desempenho de um time de futebol no último campeonato. A coluna da esquerda mostra o número de gols marcados e a coluna da direita informa em quantos jogos o time marcou aquele número de gols.
|
Gols marcados |
Quantidade de partidas |
|
0 |
5 |
|
1 |
3 |
|
2 |
4 |
|
3 |
3 |
|
4 |
2 |
|
5 |
2 |
|
7 |
1 |
Se X, Y e Z são, respectivamente, a média, a mediana e a moda desta distribuição, então
a) X = Y < Z.
b) Z < X = Y.
c) Y < Z < X.
d) Z < X < Y.
e) Z < Y < X.
Questão 05
(Enem cancelado 2009) No quadro seguinte, são informados os turnos em que foram eleitos os prefeitos das capitais de todos os estados brasileiros em 2004.
|
cidade |
turno |
|
|
1 |
Aracaju (SE) |
1º |
|
2 |
Belém (PA) |
2º |
|
3 |
Belo Horizonte (MG) |
1º |
|
4 |
Boa Vista (RR) |
1º |
|
5 |
Campo Grande (MS) |
1º |
|
6 |
Cuiabá (MT) |
2º |
|
7 |
Curitiba (PR) |
2º |
|
8 |
Florianópolis (SC) |
2º |
|
9 |
Fortaleza (CE) |
2º |
|
10 |
Goiânia (GO) |
2º |
|
11 |
João Pessoa (PB) |
1º |
|
12 |
Macapá (AP) |
1º |
|
13 |
Maceió (AL) |
2º |
|
14 |
Manaus (AM) |
2º |
|
15 |
Natal (RN) |
2º |
|
16 |
Palmas (TO) |
1º |
|
17 |
Porto Alegre (RS) |
2º |
|
18 |
Porto Velho (RO) |
2º |
|
19 |
Recife (PE) |
1º |
|
20 |
Rio Branco (AC) |
1º |
|
21 |
Rio de Janeiro (RJ) |
1º |
|
22 |
Salvador (BA) |
2º |
|
23 |
São Luís (MA) |
1º |
|
24 |
São Paulo (SP) |
2º |
|
25 |
Terezina (PI) |
2º |
|
26 |
Vitória (ES) |
2º |
Fonte: TSE. Almanaque ABRIL: Brasil 2005. São Paulo: Abril, 2005.
Na região Norte, a frequência relativa de eleição dos prefeitos no 2º turno foi, aproximadamente,
a) 42,86%.
b) 44,44%.
c) 50,00%.
d) 57,14%.
e) 57,69%.
Questão 06
(Enem 2009) Na tabela, são apresentados dados da cotação mensal do ovo extra branco vendido no atacado, em Brasília, em reais, por caixa de 30 dúzias de ovos, em alguns meses dos anos 2007 e 2008.
|
Mês |
Cotação |
Ano |
|
Outubro |
R$ 83,00 |
2007 |
|
Novembro |
R$ 73,10 |
2007 |
|
Dezembro |
R$ 81,60 |
2007 |
|
Janeiro |
R$ 82,00 |
2008 |
|
Fevereiro |
R$ 85,30 |
2008 |
|
Março |
R$ 84,00 |
2008 |
|
Abril |
R$ 84,60 |
2008 |
De acordo com esses dados, o valor da mediana das cotações mensais do ovo extra branco nesse período era igual a
a) R$ 73,10.
b) R$ 81,50.
c) R$ 82,00.
d) R$ 83,00.
e) R$ 85,30.
Questão 07
(Enem cancelado 2009) Cinco equipes A, B, C, D e E disputaram uma prova de gincana na qual as pontuações recebidas podiam ser 0, 1, 2 ou 3. A média das cinco equipes foi de 2 pontos.
As notas das equipes foram colocadas no gráfico a seguir, entretanto, esqueceram de representar as notas da equipe D e da equipe E.
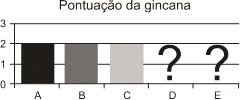
Mesmo sem aparecer as notas das equipes D e E, pode-se concluir que os valores da moda e da mediana são, respectivamente,
a) 1,5 e 2,0.
b) 2,0 e 1,5.
c) 2,0 e 2,0.
d) 2,0 e 3,0.
e) 3,0 e 2,0.
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!




