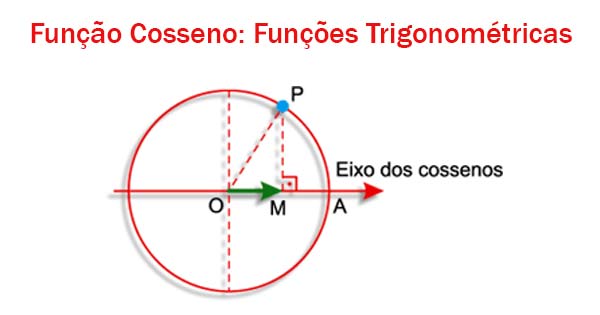
Você tem dúvidas sobre as Funções Trigonométricas? - São questões da categoria 'difícil' no Enem e nos Vestibulares. Quem acerta uma dessas já arranca na frente. Então revise os conceitos e propriedades. Aproveite também e resolva exercícios com gabarito!
Na aula de hoje as funções Seno e Cosseno serão definidas conceitualmente e geometricamente por meio dos seus gráficos. Serão abordados ainda as variações de seu sinal no ciclo trigonométrico e algumas propriedades.
Confira esta aula e arrase em matemática no Enem e nos vestibulares. É hora de mergulhar mais fundo e aprender (ou lembrar) Seno e Cosseno.
Vamos considerar o triângulo da figura abaixo: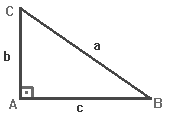
Em um triângulo retângulo, temos dois lados que formam ângulos com a hipotenusa, então para não criar confusões, denomina-se o lado sempre tomando como referência o ângulo ao qual ele está relacionado.
Para isso, acompanhe a tabela a seguir: 
O lado adjacente, na tabela acima, é o lado que descreve o ângulo junto com a hipotenusa.
Está complicando? Então, vamos dar uma parada e resolver um exercício básico de Trigonometria. Vai ajudar você a continuar.
Agora que você já entendeu o processo básico da Trigonometria, vamos trabalhar a ideia principal desse post. que é dominar Seno e Cosseno dentro do mundo da Trigonometria.
A Lei do Seno
A lei dos senos é usada quando temos um triângulo e sabemos os valores de dois ângulos e um lado. Quando temos os valores de dois lados e um ângulo, usamos a lei dos cossenos.
A lei dos senos diz o seguinte: se eu tenho um lado qualquer e divido pelo seno do ângulo que enxerga esse lado, isso é igual que um outro lado dividido pelo seno do seu ângulo. Ou seja, a fórmula da lei dos senos é: a / sen(A) = b / sen(B) = c / sen(C).
Para aplicar a lei dos senos, temos que definir qual ângulo está associado a qual lado para montar a fórmula. Para ficar mais fácil de visualizar, no vídeo, o professor Lucas faz uma demonstração de como aplicar a lei dos senos em um exercício!
Para aprender a usar a lei dos senos, veja na aula seguinte com o professor Lucas Borguesan, do canal do Curso Enem Gratuito. Ele faz vários exercícios resolvidos de trigonometria mostrando como gabaritar questões de Matemática envolvendo a lei dos senos em um triângulo!
Para continuar, veja agora o contexto que dá motivação deste estudo sobre as funções trigonométricas do Seno e do Cosseno.
Processo histórico
A essa altura, você já deve saber que a Matemática sempre andou de mãos dadas com a Astronomia, Agrimensura e as Navegações. E, por conta dessa proximidade, muitos dos problemas que surgiram com essas ciências utilizaram recursos da Álgebra e Geometria para encontrar suas respectivas soluções.
Por exemplo, no ENEM de 2009, caiu uma questão interessante que envolvia três irmãos que dividiriam uma herança com uma área de extração de ouro delimitada por uma região circular.
Se tomarmos emprestado uma parte desse problema, teríamos a seguinte figura geométrica: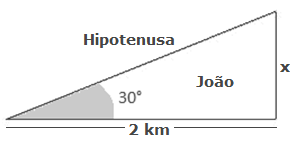
E, para encontrar o valor do lado X deste triângulo usaremos as relações trigonométricas, pois com elas podemos associar as razões entre dois lados (oposto e adjacente) a uma medida específica de cada ângulo.
No nosso caso, podemos fazer três associações:
Ângulo | 1ª Razão | 2ª Razão | 3ª Razão |
30° | x/hipotenusa | 2/hipotenusa | x/2 |
Para a 1ª razão, damos o nome de SENO.
.
.
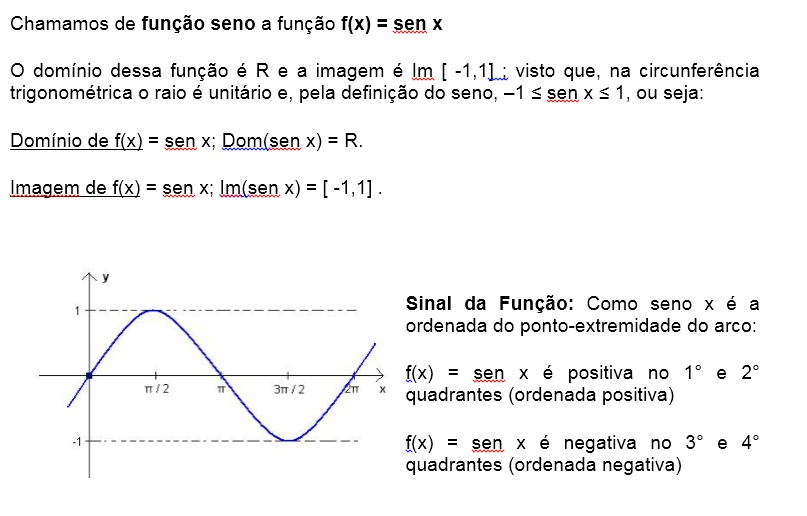
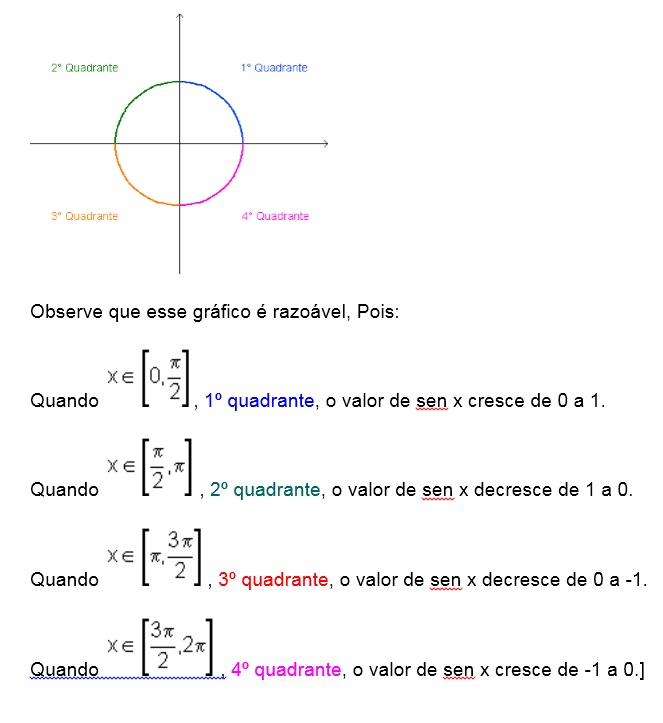
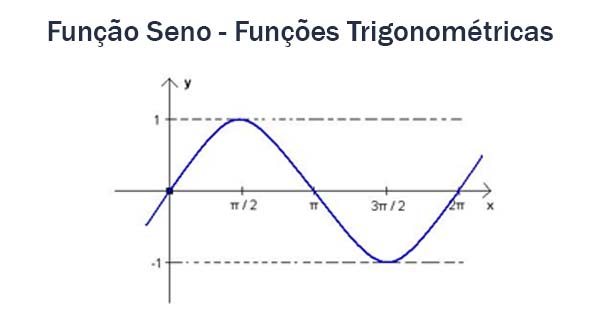
Variação da função seno
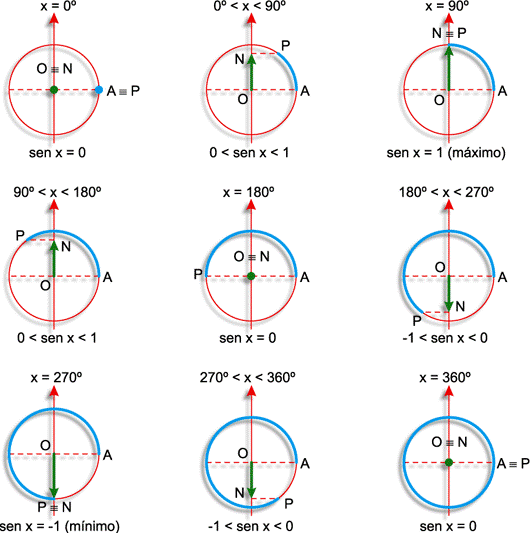
Gráfico
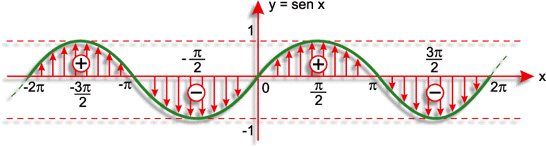
Veja a Lei do Cosseno
Acompanhe com o professor Lucas Borguesan, a Lei do Cosseno.
- A lei dos cossenos é usada quando temos um triângulo e só sabemos os valores de dois dos seus lados e o valor de um dos ângulos.
- Se for um triângulo retângulo, ou seja, um triângulo com um ângulo reto, seria possível resolver o problema com o Teorema de Pitágoras.
- Contudo, em outros tipos de retângulos é preciso aplicar a lei dos cossenos. A fórmula da lei dos cossenos, inclusive, é bastante parecida com o Teorema de Pitágoras, então é importante prestar atenção para não confundir as fórmulas.
- A fórmula da lei dos cossenos é a² = b² + c² – 2.b.c.cos(A)
- Na hora de aplicar a lei dos cossenos, lembre-se de que a “hipotenusa” é o lado oposto ao ângulo cujo valor é conhecido. Ou seja, o temos o valor do lado a e o valor do ângulo A, cujo cosseno precisamos descobrir caso o enunciado do exercício não informar.
Veja agora aplicações da Função Cosseno
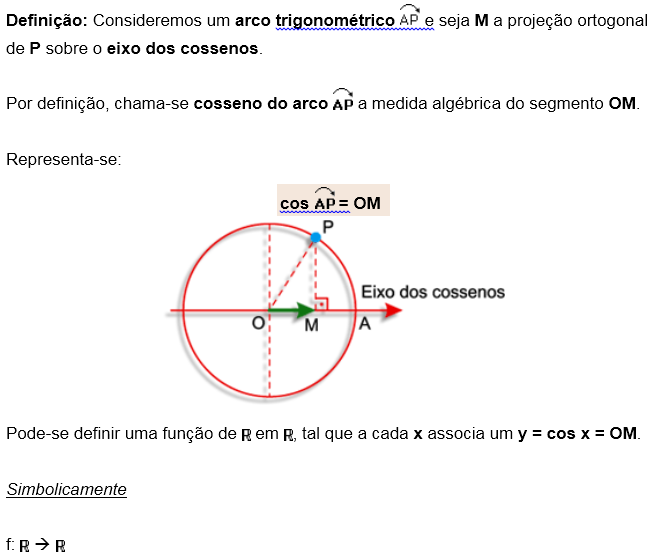
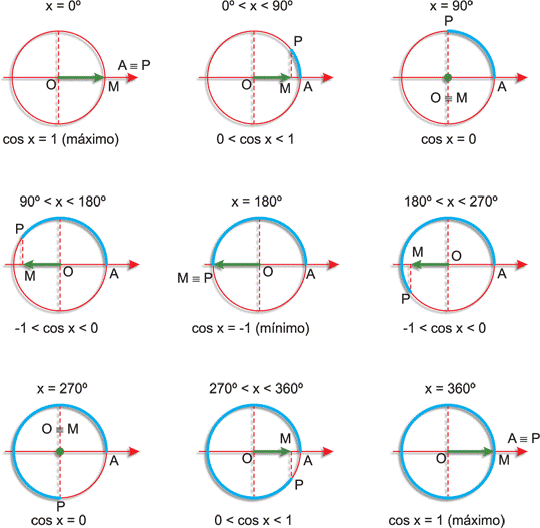
Gráfico
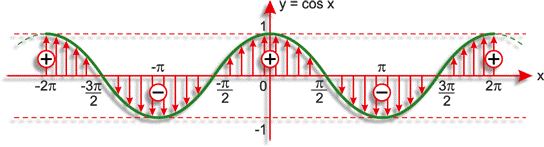
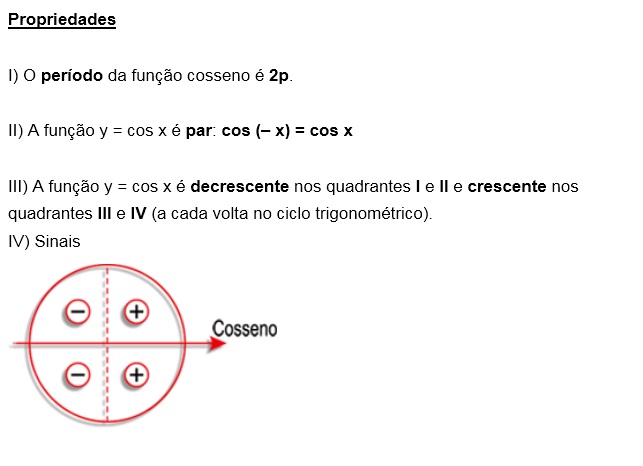
Para ajudar ainda mais nesta revisão, assista a vídeoaula abaixo e acabe com as dúvidas sobre a função cosseno. Não esqueça de resolver os exercícios!
Curso Enem Gratuito
Quer aumentar suas chances no próximo Exame Nacional do Ensino Médio e mandar bem nas Notas de Corte do Enem? Estude com as apostilas e aulas gratuitas do Curso Enem Online. Todas as matérias do Exame e ainda as Dicas de Redação. Acesse aqui o Curso Enem Gratuito Online.
Acesse aqui os Aulões do Blog do Enem! São videoaulas gratuitas e completas com os conteúdos mais relevantes para o Exame Nacional do Ensino Médio.
Os textos e exemplos acima foram preparados pela professora Jaceli Eccher para o Blog do Enem. Jaceli é formada em Matemática habilitação Licenciatura pela Universidade Federal de Santa Catarina com Especialização no ensino de Ciências pelo Instituto Federal de Santa Catarina. Facebook: https://www.facebook.com/Jacelieccher
O trecho da introdução às funções trigonométricas, no começo do post, é do professor Davi Risseti.
