O ciclo trigonométrico é a representação de uma circunferência num plano cartesiano. Ele auxilia no cálculo de razões trigonométricas como seno e cosseno. Saiba mais!
Os estudos de trigonometria estão associados à figura do triângulo retângulo e ao ciclo trigonométrico. A função do ciclo trigonométrico é estabelecer relações entre ângulos, graus, radianos, senos, cossenos e tangentes de uma circunferência.
Entenda o que é o ciclo trigonométrico e como ele pode ser cobrado no Enem e vestibulares.
O que é o ciclo trigonométrico
O círculo ou ciclo trigonométrico é uma circunferência construída sobre o plano cartesiano e que corta os eixos das abcissas e das ordenadas no ponto 1. Dessa maneira, os eixos se cruzam no ponto 0 da reta numérica e formam 4 quadrantes: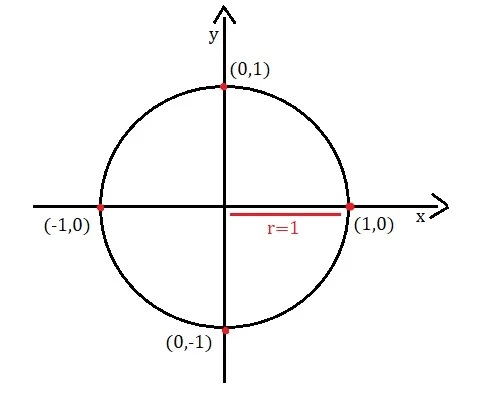
O ciclo trigonométrico possui diversos pontos que estão associados a valores de ângulos. No caso do ciclo de raio unitário, o intervalo para a localização dos ângulos é [0, 2π[, sendo que π equivale a 180º.
Dessa forma, o ciclo trigonométrico possui uma volta completa de 360º. Enquanto isso, um ângulo de 540º corresponde a uma volta inteira mais meia volta.
Ficou difícil? Então aproveita para fazer uma parada de recuperação com o professor Lucas Borguesan. Ele tem duas aulas, uma já entrando direto no Cíclo Trigonométrico, e outra que começa pelos fundamentos da trigonometria. Escolha a melhor pra você. Ou veja as duas, começando pelas relações métricas do triângulo retângulo?
O Cíclo Trigonométrico na prática
Aprenda agora na aula bem didática do professor Lucas Borguesan, do canal do Curso Enem Gratuito, para você dominar de maneira prática os segredos do Cíclo Trigonométrico:
As dicas sobre o Cíclo Trigonométrico:
- O ciclo trigonométrico é um círculo de raio 1. Ou seja, do seu cento até a borda, a medida é 1.
- Assim, podemos definir todos os valores de seno e cosseno que existem, uma vez que o círculo trigonométrico compreende todos os ângulos.
- Na trigonometria, seno e cosseno são chamados de razões trigonométricas.
- Para medir o valor do seno, é comum usar o eixo vertical do círculo trigonométrico. Desta forma, o eixo vertical do ciclo trigonométrico é chamado eixo dos senos.
- Por outro lado, podemos encontrar o valor do cosseno no eixo horizontal, de maneira que este é chamado de eixo dos cossenos.
- Veja novamente o resumo acima, para você dominar e mandar bem no Enem.
As Relações Métricas do Triângulo
Agora, veja os Fundamentos básicos para a Trigonometria, que começam com as Relações Métricas doo Triângulo Retângulo:
- Você já sabe que o triângulo retângulo é uma referência nas aplicações que envolvem a geometria plana.
- Em algumas profissões ficaria difícil entender diferentes fenômenos se não usássemos suas diferentes aplicações.
- Seu ângulo reto, suas relações métricas e trigonométricas dão ferramentas para cálculos de distâncias muito grandes como entre dois planetas, por exemplo.
- Nesta aula acima, o professor Lucas te ensina tudo sobre as relações trigonométricas do triângulo retângulo, te mostra como calcular seno, cosseno e tangente, explica a tabela dos ângulos notáveis e te dá dicas e macetes para agilizar seus cálculos.
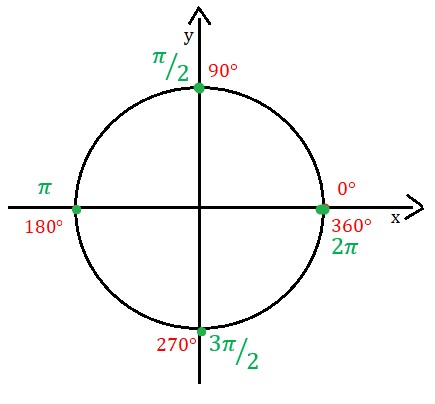
Ângulos e quadrantes do ciclo trigonométrico
O ciclo trigonométrico possui os seguintes referenciais na localização dos ângulos: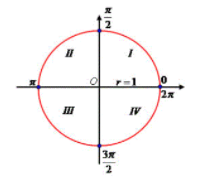
- Quadrante I: 0º < x < 90º ou 0 < x < π/2
- Quadrante II: 90º < x < 180º ou π/2 < x < π
- Quadrante III: 180º < x < 270º ou π < x < 3π/2
- Quadrante IV: 270º < x < 360º ou 3π/2 < x < 2π
Além dos quadrantes, ainda temos os ângulos principais:
Já em relação aos quadrantes e os eixos x e y, lembre-se da seguinte relação: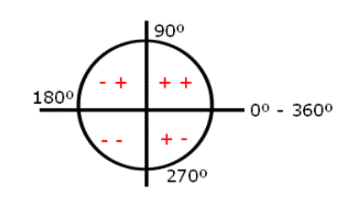
Os sinais de mais (+) e de menos (-) indicam o sinal de cada quadrante em relação ao seu respectivo eixo. Perceba que no 1º quadrante temos dois sinais positivos. O primeiro sinal é referente ao eixo x, ou seja, o eixo horizontal. Já o segundo sinal é referente ao eixo y, ou seja, o eixo vertical.
Note que o 1º quadrante está localizado ao lado direito do eixo horizontal, o que significa que está d0 lado positivo. Também está localizado na parte superior do eixo y, que é sua camada positiva. Portanto, o 1º quadrante está localizado positivamente nos eixos x e y do plano cartesiano. É por isso que ele possui dois sinais positivos, um indicando o eixo x e outro o eixo y.
Já o 2º quadrante está localizado na parte negativa do eixo horizontal, pois está à sua esquerda. Mas note que o 2º quadrante está localizado acima do eixo vertical. Por isso ele é positivo.
O 3º quadrante encontra-se à esquerda do eixo x e na parte inferior do eixo y, o que significa que ele é negativo em ambas as posições.
Por fim, o 4º quadrante está à direita do eixo x, logo é positivo. Contudo, está localizado na parte inferior do eixo y, tornando-se negativo nesta localização.
Exemplos
Os cálculos a seguir são efetuados com o objetivo de localizar ângulos nos quadrantes do círculo trigonométrico.
Exemplo 1
Em qual quadrante está localizado o ângulo de 600º?
Resolução: a fim de descobrir a posição do ângulo é necessário dividir 600º por 360º. Em seguida, é necessário verificar o valor correspondente ao resto, pois é ele que indicará o quadrante de localização.
Fazendo o cálculo 600/360 obtemos 1 com resto igual a 240. Portanto, o ângulo de 600º está localizado no 3º quadrante. Lembre-se que o 3º quadrante abrange os ângulos entre 180º e 270º.
Exemplo 2
O ângulo 1540º está localizado em qual quadrante?
Resolução: 1540/360 = 4 e resto igual a 100. Assim, concluímos que 1540º corresponde a 4 voltas completas, estando localizado no ponto equivalente a 100º. Portanto, está localizado no 2º quadrante.
Radianos no ciclo trigonométrico
Além dos graus, existem os radianos no ciclo trigonométrico. Para você entender a equivalência entre graus e radianos, lembre-se que um π radianos corresponde a 180º. Assim:
- Uma volta completa equivale a 360º e 2π radianos;
- Meia volta equivale a 180º e π radianos;
- Um quarto de volta equivale a 90º e π/2 radianos;
- Três quartos de volta equivalem a 270º e 3π/2 radianos.
Então, toda vez que você tiver que transformar graus em radianos ou vice-versa, você pode fazer uma destas duas operações:
- Lembrar que um π radianos corresponde a 180º e fazer uma regra de 3.
- Construir o ciclo trigonométrico levando em conta a posição dos quadrantes, sentido e congruência.
Seno e cosseno
O seno e o cosseno são algumas das relações trigonométricas que podem ser representadas no ciclo trigonométrico. Esta relação é dada entre os pontos no arco que representam os ângulos e os próprios eixos x e y.
Seno
O seno é a reflexão do ponto no eixo das ordenadas. A fim de entender melhor, imagine que uma lanterna está localizada ao lado do ciclo trigonométrico. A sombra que o ponto da circunferência faz no eixo y é o valor do seno daquele ângulo. Veja no exemplo com o ângulo de 30º:
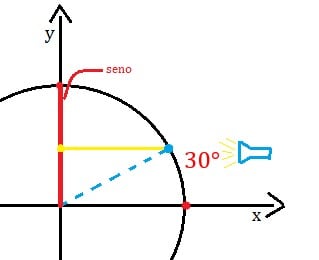
Você se lembra que no início deste post dissemos que o raio do ciclo trigonométrico é sempre igual a 1? Então observe na imagem que a sombra do ponto que representa o ângulo de 30º atinge o eixo dos senos exatamente na metade. Logo, podemos concluir que o seno de 30º é igual a 1/2.
Cosseno
O mesmo raciocínio é utilizado para obtenção dos cossenos. A diferença é que agora a reflexão do ponto é no eixo x, representando o valor do cosseno naquele ângulo. Assim, é só imaginar que a lanterna está iluminando de cima para baixo: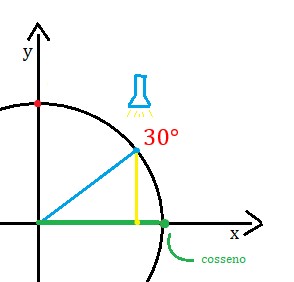
Agora, somente visualizando a imagem, ficou um pouco mais difícil de estimar qual é o cosseno de 30º refletido no eixo x, não é? Mas com uma observação mais minuciosa é possível perceber um triângulo retângulo e, através dele, calcular os valores do cosseno.
Essa visualização nos leva a um ponto bem importante que é o sinal do cosseno e o sinal do seno em cada um dos quadrantes. Visto que o ciclo trigonométrico é posicionado sobre um plano cartesiano, tanto o sinal do seno quanto do cosseno obedecem ao sinal do eixo no qual estão projetados.
Sendo assim: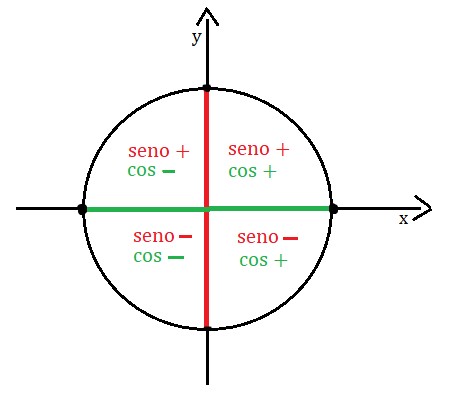
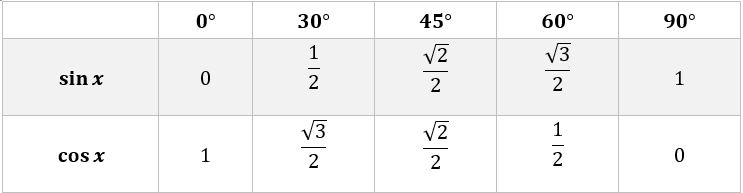
Ângulos notáveis
Os ângulos mais utilizados em cálculos costumam ser 0º, 30º, 45º, 60º e 90º. Esses são os chamados ângulos notáveis e possuem os seguintes valores para seno e cosseno:
Videoaula
Exercícios sobre ciclo trigonométrico
1- (ENEM/2018)
A rosa dos ventos é uma figura que representa oito sentidos, que dividem o círculo em partes iguais.
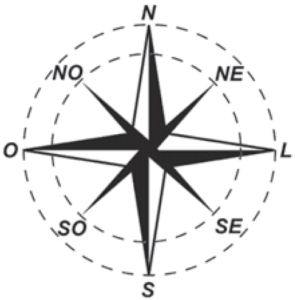
Uma câmera de vigilância está fixada no teto de um shopping e sua lente pode ser direcionada remotamente, através de um controlador, para qualquer sentido. A lente da câmera está apontada inicialmente no sentido Oeste e o seu controlador efetua três mudanças consecutivas, a saber:
1ª mudança: 135º no sentido anti-horário;
2ª mudança: 60º no sentido horário;
3ª mudança: 45º no sentido anti-horário.
Após a 3ª mudança, ele é orientado a reposicionar a câmera, com a menor amplitude possível, no sentido Noroeste (NO) devido a um movimento suspeito de um cliente.
Qual mudança de sentido o controlador deve efetuar para reposicionar a câmera?
a) 75º no sentido horário.
b) 105º no sentido anti-horário.
c) 120º no sentido anti-horário.
d) 135º no sentido anti-horário.
e) 165º no sentido horário.
2- (UFRR/2015)
Conforme apresentado na figura, a seguir, por meio de um dispositivo, articularam-se dois discos, A (maior) e B (menor). O disco B gira dentro do disco A, e o raio de B é igual à metade da medida do raio de A; a seta coincide com o diâmetro do disco B, e indica um ângulo central.
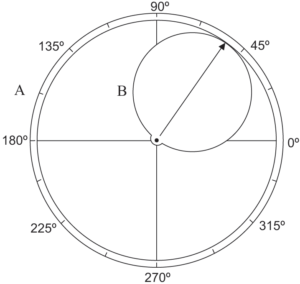
Os comprimentos dos segmentos determinados pelas interseções da borda do disco B com os eixos perpendiculares do disco A indicam os valores de quais funções trigonométricas?
a) seno e tangente;
b) seno e secante;
c) seno e cosseno;
d) cosseno e secante;
e) cosseno e tangente.
3- (UFJF MG/2015)
No processo de calcular o ângulo x formado entre duas avenidas transversais, um engenheiro obteve a seguinte equação sen x = sen3x. Sabendo que x não excede 180º, é CORRETO afirmar que:
a) x = –1
b) x = 0
c) x = 1
d) x = π/2
e) x = 3π/2
Gabarito:
- E
- C
- D
