O triângulo retângulo tem um ângulo de 90º, cateto oposto, cateto adjacente e hipotenusa. Partem daí as relações trigonométricas. Veja a origem no Teorema de Pitágoras
Em primeiro lugar você precisa saber o que significa um triângulo retângulo. Além disso, você vai estudar aqui a área do triângulo retângulo, as relações métricas e trigonometria. Então vamos lá:
O que é o triângulo retângulo?
- Por definição, esse triângulo é aquele que possui um ângulo reto (igual a 90º) e dois outros ângulos agudos.
- Além disso, a soma dos ângulos internos é de 180 graus, o que corresponde a um ângulo raso.
- Os lados desse triângulo apresentam nomes específicos.
- Assim, os lados que formam o ângulo reto são denominados de catetos
Já o lado oposto ao ângulo reto é denominado hipotenusa.
Da mesma forma, você podes constatar isso na imagem, onde A-C e B-C são os dois catetos, enquanto A-B é a hipotenusa: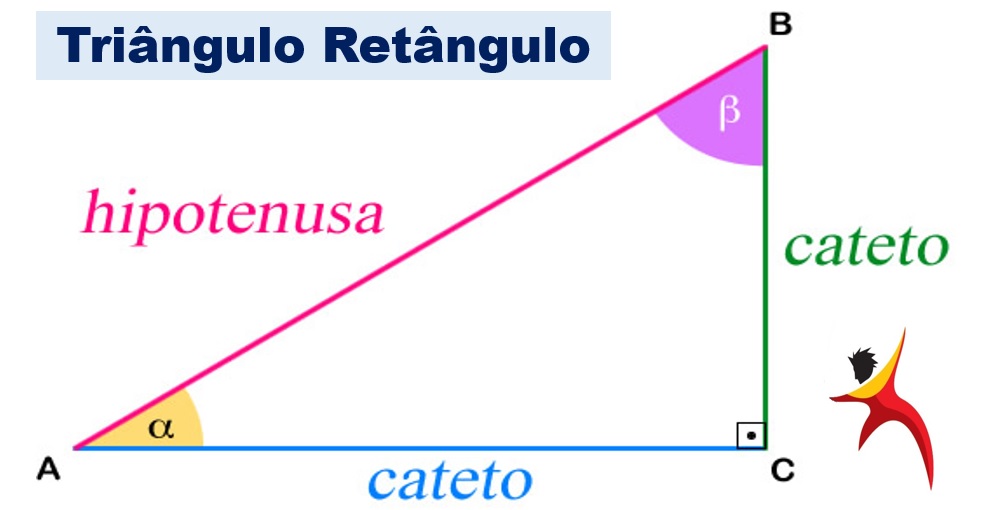 Esquema representando os nomes dos lados de um triângulo retângulo. O que fica “de frente” para o ângulo reto se chama hipotenusa. Os outros dois são os catetos.
Esquema representando os nomes dos lados de um triângulo retângulo. O que fica “de frente” para o ângulo reto se chama hipotenusa. Os outros dois são os catetos.
Introdução ao triângulo retângulo
O triângulo retângulo no universo da matemática é uma das figuras geométricas mais utilizadas para solucionar problemas que envolvem cálculos de ângulos, lados, área e etc.
- Apesar dessa aula ser focada no triângulo retângulo, devemos lembrar que existem outros tipos de triângulos.
- É o caso dos isósceles, escaleno e equilátero.
- Também pode existir um triângulo retângulo isósceles.
- Nesse sentido, esse triângulo retângulo isósceles apresenta os catetos de mesma medida.
Relações métricas no triângulo retângulo
As relações métricas do triângulo retângulo relacionam as medidas dos seus lados e suas projeções. Para entender, vamos representar esse triângulo apoiado, por exemplo, sobre a hipotenusa: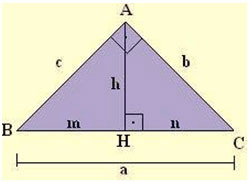 Imagem de um triângulo dividido em dois triângulos menores internamente. Os dois triângulos menores possuem um ângulo de noventa graus.
Imagem de um triângulo dividido em dois triângulos menores internamente. Os dois triângulos menores possuem um ângulo de noventa graus.
Nessa representação temos:
- Hipotenusa = a
- Catetos = b e c
- Altura relativa à hipotenusa = h
- Projeções dos catetos sobre a hipotenusa = m e n
Leia também
Relações métricas e o Teorema de Pitágoras
Antes de tudo, você já deve ter escutado a famosa fórmula do Teorema de Pitágoras, certo? Pois bem, ele está relacionado às relações métricas no triângulo retângulo.
1) Teorema de Pitágoras: hip 2 = cat 1 + cat 2
Em outras palavras a representação da fórmula: a soma do quadrado dos catetos é igual ao cateto da hipotenusa. Agora, observe a representação do Teorema de Pitágoras atuando nos cálculos: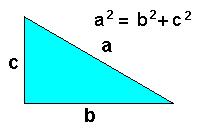 fórmula do teorema de Pitágoras expressa em um triângulo retângulo
fórmula do teorema de Pitágoras expressa em um triângulo retângulo
Observe na demonstração gráfica do Teorema de Pitágoras na imagem abaixo que se você ‘somar as áreas geradas pelos quadrados dos catetos’ vai encontrar exatamente a mesma ‘área gerada pelo quadrado da hipotenusa’.
Veja esta imagem a seguir com calma. Trabalhe mentalmente esta representação gráfica para compreender o Teorema de Pitágoras. Nunca mais você esquece esta característica do triângulo retângulo: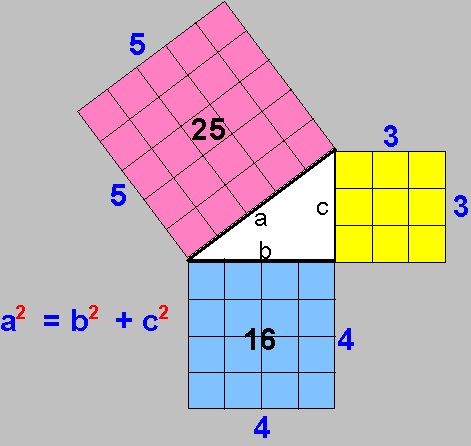
Observe a quantidade de quadradinhos dentro da área quadrada que se forma com o lado de cada um dos catetos (quadrado amarelo + quadrado azul). Somando esses dois quadrados coloridos, temos 25 quadradinhos, certo?
Assim, você percebe rapidamente que a quantidade dessa soma é igual ao número de quadradinhos do quadrado rosa. Portanto, temos aí o Teorema de Pitágoras.
Cálculo da área no triângulo retângulo
Como falamos, esse triângulo conta com um ângulo reto (90º) e dois ângulos menores (conhecidos como agudos). Assim, das 3 alturas encontradas nesse tipo de triângulo, duas coincidem com os lados desse triângulo.
Veja no esquema abaixo como ficaria a fórmula da área do triângulo retângulo: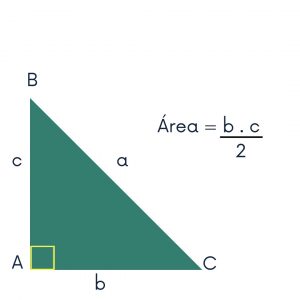 Fórmula usada para calcular a área do triângulo retângulo.
Fórmula usada para calcular a área do triângulo retângulo.
Trigonometria
Na solução de alguns problemas, aplicamos fórmulas denominadas de razões trigonométricas no triângulo retângulo. Elas são aquelas conhecidas como seno, cosseno e tangente. Frequentemente aparecem no vestibular e no Enem, ou seja, é muito importante que você as tenha na cabeça.
A fórmula do seno é expressa por cateto oposto dividido pela hipotenusa.
Já o cosseno é o cateto adjacente dividido pela hipotenusa.
Por fim, a tangente é o cateto oposto dividido pelo cateto adjacente.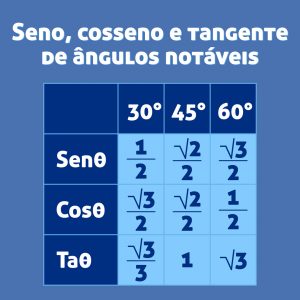 Tabela de razões trigonométricas dos ângulos mais utilizados.
Tabela de razões trigonométricas dos ângulos mais utilizados.
Na tabela, você pode ver os valores da trigonometria no triângulo retângulo com os ângulos mais utilizados em exercícios. Essas fórmulas também são frequentemente chamadas de relações trigonométricas no triângulo retângulo.
Veja agora uma videoaula com exercícios de triângulo retângulo:
Outras relações métricas:
- a) Cateto x Cateto = Hipotenusa x Altura (b x = a x h)
- b) Cateto 2 = Hipotenusa x Projeção
- (b2 = a x n) ou (c2 = a x m)
- c) Altura 2 = Projeção x Projeção
- (h 2 = m x n)
Triângulo retângulo: exercício resolvido
Por exemplo: Na figura abaixo, sabendo-se que AB = 6 cm e AC = 8 cm, determine as medidas de BC, BH, HC e AH.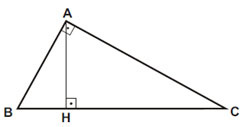 Solução:
Solução:
- a) BC2 =AB2+ AC 2
 62 + 82 = 36 + 64 = 100BC = √100 = 10
62 + 82 = 36 + 64 = 100BC = √100 = 10 - b) AB x AC = BC x AH
 6 x 8 = 10 x AH
6 x 8 = 10 x AH AH = 4,8
AH = 4,8 - c) AB2 = BH x BC
 62 = BH x 10
62 = BH x 10  BH = 3,6
BH = 3,6 - d) AC2 = CH x BC
 82 = CH x 10
82 = CH x 10  CH = 6,4
CH = 6,4
Logo depois de finalizar o exercício, confira suas respostas e veja se você as marcou corretamente. Dessa forma, você garante o sucesso na prova e não erra questões bobas. Frequentemente alunos trocam o sinal, por exemplo e acabam deslizando na prova.
Exercícios sobre triângulo retângulo do Enem
Veja como o conteúdo de triângulo retângulo costuma cair no Enem. Resolva os exercícios abaixo e prepare-se para as provas.
Questão 01 – (ENEM/2019)
A unidade de medida utilizada para anunciar o tamanho das telas de televisores no Brasil é a polegada, que corresponde a 2,54 cm. Diferentemente do que muitos imaginam, dizer que a tela de uma TV tem X polegadas significa que a diagonal do retângulo que representa sua tela mede X polegadas, conforme ilustração.
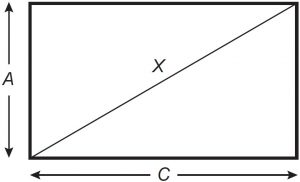
O administrador de um museu recebeu uma TV convencional de 20 polegadas, que tem como razão do comprimento (C) pela altura (A) a proporção 4 : 3, e precisa calcular o comprimento (C) dessa TV a fim de colocá-la em uma estante para exposição.
Portanto, a tela dessa TV tem medida do comprimento C, em centímetro, igual a
a) 12,00.
b) 16,00.
c) 30,48.
d) 40,64.
e) 50,80.
Gab: D
Questão 02 – (ENEM/2018)
Um quebra-cabeça consiste em recobrir um quadrado com triângulos retângulos isósceles, como ilustra a figura.

Uma artesã confecciona um quebra-cabeça como o descrito, de tal modo que a menor das peças é um triângulo retângulo isósceles cujos catetos medem 2 cm.
O quebra-cabeça, quando montado, resultará em um quadrado cuja medida do lado, em centímetro, é quadrado cuja medida do lado, em centímetro, é
a) 14
b) 12
c) 7√2
d) 6 + 4√2
e) 6 + 2√2
Gab: A
Questão 03 – (ENEM/2017)
Uma família possui um terreno retangular com 18 metros de largura e 24 metros de comprimento. Foi necessário demarcar nesse terreno dois outros iguais, na forma de triângulos isósceles, sendo que um deles será para o filho e o outro para os pais. Além disso, foi demarcada uma área de passeio entre os dois novos terrenos para o livre acesso das pessoas.
Os terrenos e a área de passeio são representados na figura.

A área de passeio calculada pela família, em metro quadrado, é de
a) 108.
b) 216.
c) 270.
d) 288.
e) 324.
Gab: A
Questão 04)
A figura mostra um edifício que tem 15 m de altura, com uma escada colocada a 8 m de sua base ligada ao topo do edifício. Portanto, o comprimento dessa escada é de: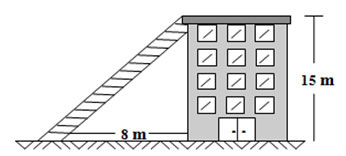
a) 12; b) 30; c) 15; d) 17; e) 20
Questão 05)
A prefeitura de uma cidade deseja construir um Posto de Saúde e uma Escola em um terreno retangular de lados AB = 150 m e BC = 80 m, de acordo com a figura abaixo:
O Posto de Saúde deve ficar sobre o lado AB à uma distância de 120m do vértice B e a Escola sobre o lado CD à uma distância de 70 m do vértice D. A prefeitura planeja a construção de um acesso passando por dentro desse terreno no sentido de diminuir a distância entre a Escola e o Posto de Saúde.
Assim, o valor mais próximo da extensão desse acesso é de:
a) 100 m; b) 90 m; c) 70 m; d) 60 m; e) 110 m
 6
6 6 x 8 = 10 x AH
6 x 8 = 10 x AH AH = 4,8
AH = 4,8 6
6 BH = 3,6
BH = 3,6 8
8 CH = 6,4
CH = 6,4


