Figuras planas possuem duas dimensões: comprimento e largura. A área mede o tamanho que uma figura ocupa numa superfície e o perímetro mede seu contorno.
Geometria plana é um dos assuntos de Matemática que mais caem no Enem, vestibulares e Encceja. Por isso é importante começar a estudar desde conteúdos básicos, como figuras planas, e ir até conteúdos mais avançados, como relações trigonométricas. Nesta aula você vai aprender o que são e quais são as figuras planas, quais são seus elementos e a calcular seu perímetro e área.
O que são figuras planas
Uma figura plana nada mais é que uma região plana fechada por segmentos de reta (no mínimo três segmentos). Em outras palavras, figuras planas são aquelas que possuem apenas duas dimensões: comprimento e largura.
Além disso, todas as figuras planas com três ou mais lados são chamadas de polígonos. Cada uma dessas formas geométricas possui fórmulas matemáticas específicas para o cálculo da medida de seus perímetros e de suas superfícies (ou áreas).
Em contrapartida, figuras geométricas espaciais – também conhecidas como sólidos geométricos ou poliedros – são aquelas que possuem 3 dimensões: comprimento, largura e altura.
Quais são as figuras planas
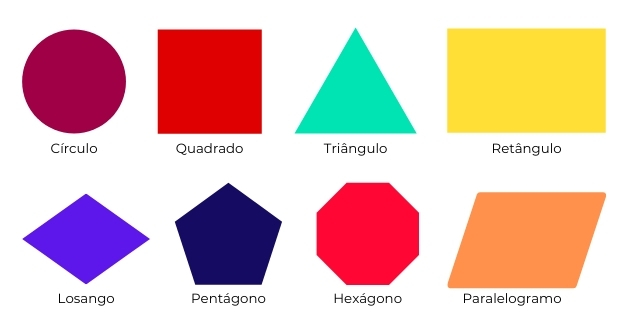
Na geometria, as formas mais conhecidas de figuras planas são: círculo, quadrado, triângulo, retângulo, trapézio, hexágono, pentágono, paralelogramo e losango.
Leia também
Elementos de um polígono
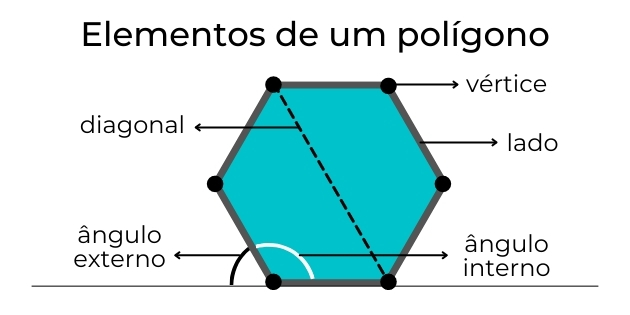
Existem 5 elementos principais em um polígono ou figura plana: vértices, lados, diagonais, ângulos internos e ângulos externos. O vértice é como se fosse o “canto” ou “esquina” do polígono. Ao ligar dois vértices consecutivos através de uma reta, obtemos um lado.
Enquanto isso, se você fizer a junção de dois vértices que não são consecutivos, você irá obter uma diagonal. Também é possível formar ângulos na parte de dentro do polígono ou figura plana. Esses são chamados de ângulos internos. Se prolongarmos o ângulo para a parte de fora do polígono, ele passa a ser o ângulo externo. Observe a imagem a seguir para entender melhor.
É possível que você encontre questões no Enem ou nos vestibulares que exijam que você saiba calcular o número de lados ou de diagonais de uma figura plana, mas sem te dizer qual é. Para que você consiga resolver esse tipo de problema existe uma fórmula simples:
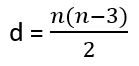
Onde:
- d = número de lados do polígono
- n = número de diagonais do polígono
Videoaula sobre figuras planas
Para ver exemplos desse cálculo e aprofundar o conteúdo visto até aqui, confira esta aula sobre figuras planas no canal do Curso Enem Gratuito:
Perímetro de uma figura geométrica plana
O perímetro de uma figura geométrica plana é a soma das medidas de todos os lados dessa figura. Portanto, quando você dá a volta num campo de futebol caminhando sobre as quatro linhas que demarcam o gramado, você percorreu a distância do perímetro do campo.
Ou, quando você dá a volta numa praça caminhando sobre a linha do meio-fio que separa a praça da rua, por exemplo, você percorreu o perímetro da praça. O campo de futebol ou a praça estão demarcados por linhas que formam figuras planas.
Vamos ver um exemplo para ficar mais fácil. Observe a figura abaixo: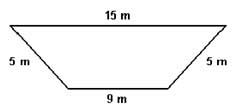
Ela representa uma figura plana de quatro lados – um quadrilátero – denominada trapézio. Então, como você pode ver, as medidas de seus lados valem 15 cm, 5 cm, 9 cm e 5 cm. Como conhecemos todas as medidas dos lados da figura, podemos calcular o perímetro através da soma dos lados:
Soma dos lados = 15 + 5 + 9 + 5 = 34 cm.
O perímetro é uma grandeza cuja unidade de medida é a de comprimento e, portanto, pode ser medido em metros ou em seus múltiplos e submúltiplos.
Perímetro de uma circunferência
A circunferência possui infinitos lados e, por isso, o cálculo do perímetro possui uma fórmula especial:
P = 2 . π . r
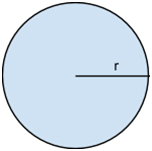
Lembre-se de que r é o raio da circunferência e o valor de π equivale a 3,14.
Área de uma figura geométrica plana
Área é a denominação dada à medida de uma superfície. Cada uma das figuras planas possui uma fórmula específica para o cálculo de sua área. Vamos conhecer cada uma delas em seguida.
Área do quadrado e do retângulo
O cálculo da área (A) de um retângulo, de um quadrado ou de um paralelogramo é feita pela multiplicação entre a medida da base (b) (comprimento) e a medida da altura (h) (largura).
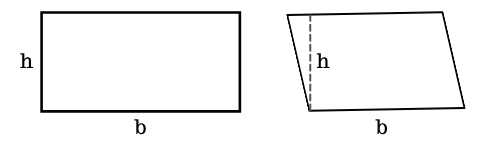
Portanto, a fórmula para o cálculo de um retângulo é A = b . h.
Como o quadrado tem todos os lados (l) iguais, podemos escrever a fórmula de duas maneiras: A = l . l ou A = l².
Área do triângulo
A fim de entender a fórmula do cálculo da área do triângulo, você pode imaginar que um retângulo dividido ao meio forma dois triângulos:
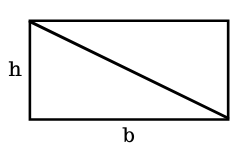
É por isso que para calcular a área do triângulo basta multiplicar a base (b) pela altura (h) e dividir o resultado por 2. Assim, a fórmula é a seguinte: A = (b . h) / 2.
Área do círculo
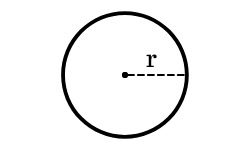
A área de um círculo pode ser calculada por meio da seguinte fórmula: A = π . r². Sendo que r é o raio do círculo e π (Pi) tem o valor de 3,141592…
Área do losango
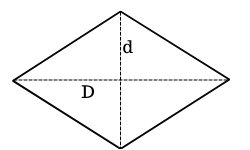
O losango é uma das figuras planas em que se utilizam as medidas das diagonais para calcular a área. Dessa forma, para calcular a área de um losango basta multiplicar a diagonal maior (D) pela diagonal menor (d), e dividir por 2, resultando na fórmula: A = (D . d) / 2.
Área do trapézio
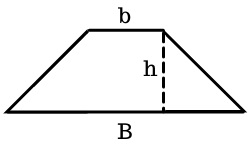
Por fim, para calcular a área do trapézio é necessário somar o valor das duas bases – base maior (B) e base menor (b) –, multiplicar pela altura (h) e dividir por 2. Assim, temos a fórmula A = [(B + b) . h]/2.
Para finalizar seus estudos, assista ao vídeo a seguir em que o prof. Sarkis resolve questões de figuras planas e responda aos exercícios:
Exercícios sobre figuras planas
1 – (Faculdade Santo Agostinho BA/2020)
Beatriz quer colocar uma fita decorativa ao redor do tampo de uma mesa redonda.
SHUTTERSTOCK/Zonda
Para calcular o perímetro da mesa, ela considerou π = 3,1416. Se o raio da mesa é 95 cm, então o valor inteiro, aproximado, do perímetro da mesa, em metros, é
a) 4 m.
b) 5 m.
c) 6 m.
d) 59 m.
e) 60 m.
2 – (IFAL/2019)
Um terreno tem o formato de um triângulo retângulo cuja dimensão de um dos catetos mede 5 m e a dimensão da sua hipotenusa mede 13 m. Qual é a área desse terreno em metros quadrados?
a) 12,5
b) 25
c) 30
d) 32,5
e) 35
3 – (UNIRG TO/2020)
No livro intitulado “Elementos”, do matemático grego Euclides de Alexandria (300 a.C), há um quadrado de lado a, a partir do qual Euclides procura encontrar a área de outro quadrado, destacado em cinza, na figura a seguir.
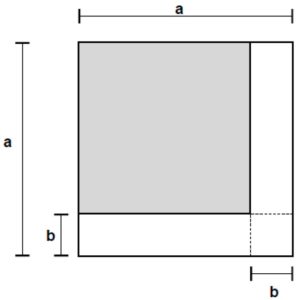
Desse modo, a área do quadrado destacado em cinza na figura é obtida pela expressão:
a) a2 = (a – b)2 + 2ab
b) a2 = (a – b)2 – 2ab
c) (a – b)2 = a2 + b2 – 2ab
d) (a + b)2 = a2 + b2 + 2ab
4 – (UECE/2014)
Se, em um polígono convexo, o número de lados n é um terço do número de diagonais, então o valor de n é
a) 9.
b) 11.
c) 13.
d) 15.
5- (IFBA/2019)
Um terreno retangular com 100 metros de frente e x metros de lateral foi dividido entre dois amigos A e B de tal forma que a área de A ficou igual a uma vez e meia área de B. Na divisão, os dois mantiveram a medida x nas suas laterais de forma que a divisão se deu por um segmento de reta com uma extremidade na frente do terreno e outra no fundo. Determine o comprimento, em metros, da frente do terreno de B, sabendo que o comprimento do fundo do terreno de A é igual a 30 metros.
a) 12
b) 24
c) 6
d) 36
e) 10
Gabarito:
- C. Resolução: O perímetro do disco é P = 2, com = 3,1416 e r = 95 cm. Temos que P = 2 x 3,1415 cm x 95 cm = 596,904 cm 5,97 m, arredondando para um número inteiro, P = 6 m
- C
- C
- A
- E
