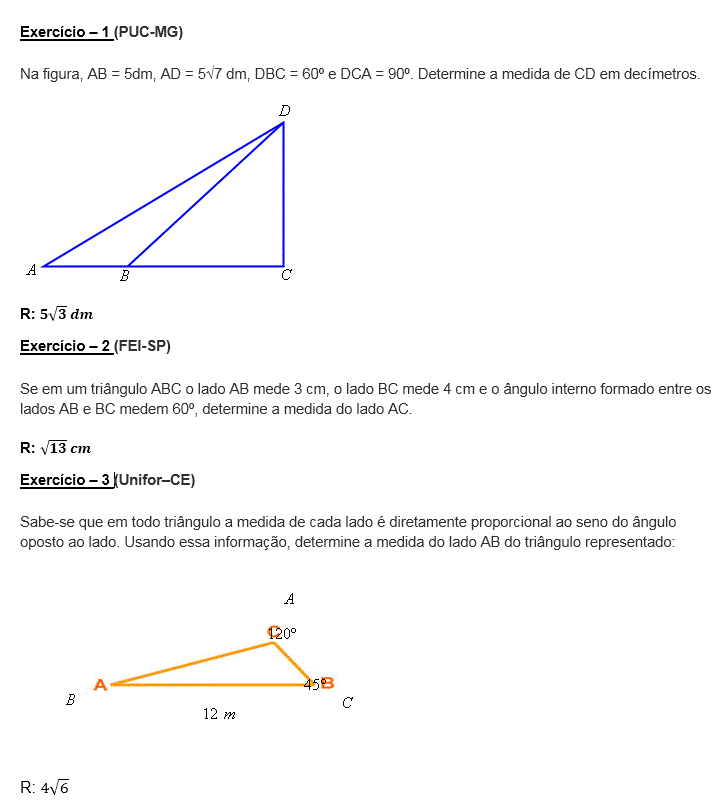
Veja a diferença entre um triângulo equilátero e um triângulo escaleno. Domine a classificação dos triângulos e as propriedades fundamentais do Triângulo Reto com o Teorema de Pitágoras.
Matemática Enem: O triângulo é considerado uma importante figura no ramo da Geometria, pois através dele podemos estabelecer várias relações fundamentais. Como exemplo temos uma relação muito importante utilizada na Geometria e na Trigonometria, que é o Teorema de Pitágoras. Nesta aula você vai conhecer a Classificação dos Triângulos e suas propriedades.
Podemos definir o triângulo como um polígono formado por três segmentos de retas que se cruzam duas a duas, formando três vértices, três ângulos e três lados. A palavra “triângulo” tem origem do latim triangulu, e é um polígono que possui três lados e três ângulos.
Observe a 0 figura a seguir, e leia novamente o parágrafo acima, e compare com a figura. É mais simples de entender assim, e você vai conseguir.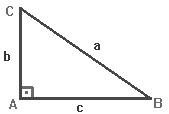
Os triângulos se classificam quanto ao tamanho da medida dos seus lados e quanto à medida de seus ângulos. Estes fatores interferem também na Classificação dos Triângulos.
A Classificação dos Triângulos
O Triângulo é o polígono com o menor número de lados, e é também o único polígono que não possui diagonais. Cada ângulo externo do triângulo é suplementar ao ângulo interno adjacente. Complicou de entender? Calma, que tem solução.
Veja agora um resumo inicial sobre a Classificação e Propriedades dos Triângulos. Confira com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito.
Como você já sabe, o triângulo é uma figura plana formada por três segmentos de retas. Serão estudados nesta aula os elementos geométricos que compõem essa figura bem como as propriedades pertinentes a esses elementos.
Os triângulos podem ser obtidos de diversas formas, a mais usual delas é desenhar 3 pontos não colineares (pontos que não pertencem a uma mesma reta) e ligá-los com segmentos de reta.
Alguns triângulos têm destaque na natureza e no dia a dia das pessoas por serem mais recorrentes, como é o caso dos triângulos retângulos que possuem um ângulo reto, isto é, um ângulo igual a 90 graus. Também ocorrem com frequência e possuem propriedades interessantes os triângulos isósceles e equiláteros
Elementos de um triângulo
Na figura identificam-se os seguintes elementos: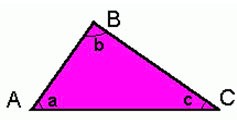
- 1) Vértices: são os pontos A, B e C
- 2) Ângulos internos: a, b e c
- 3) Lados: AB, AC e BC
Altura
Altura: é um segmento de reta traçado a partir de um vértice de forma a encontrar o lado oposto ao vértice formando um ângulo reto (90º). BH é uma altura do triângulo.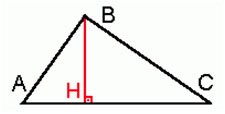
Ângulo Externo
O Ângulo externo é formado por um dos lados do triângulo e pelo prolongamento do lado adjacente.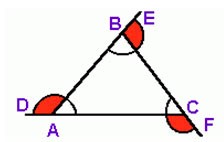
Na figura são ângulos externos os ângulos D, E, F.
Propriedades dos Triângulos
- 1) A soma dos ângulos internos de qualquer triângulo é sempre igual a 180º.
- 2) A soma dos ângulos externos de qualquer triângulo é sempre igual a 360º.
- 3) Cada ângulo externo é igual à soma dos outros dois internos não adjacentes a ele.
- 4) O maior lado do triângulo está sempre oposto ao maior ângulo desse triângulo.
Classificação de um triângulo quanto à medida de seus lados
- Triângulo equilátero: possui os três lados com medidas iguais.
- Triângulo isósceles: possui dois lados com medidas iguais.
Triângulo escaleno: possui os três lados com medidas diferentes.
Classificação dos triângulos quanto à medida dos ângulos
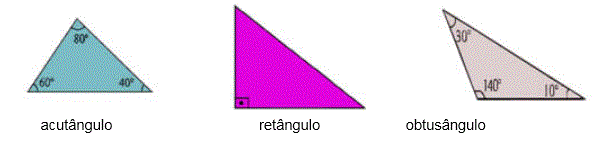
Triângulo acutângulo: possui todos os ângulos com medidas menores que 90º.
Triângulo retângulo: possui um ângulo com medida igual a 90º.
Triângulo obtusângulo: possui um ângulo obtuso, maior que 90º.
A Base do Triângulo
OBS.: 1) Denomina-se base o lado sobre qual se apoia o triângulo.
OBS.: 2) No triângulo isósceles, considera-se base o lado de medida diferente e sobre ele estarão localizados os ângulos congruentes (iguais) do triângulo.
Propriedades dos triângulos isósceles
1- Em um triângulo isósceles, os ângulos da base são congruentes
Para verificar essa propriedade basta lembrar que os triângulos ACD e BCD são congruentes e os ângulos da base, “f” e “g”, são também congruentes por serem correspondentes.
2- A altura de um triângulo isósceles, relativa à base, é também mediana e bissetriz
- Desenhe a altura do triângulo isósceles ABC. Repare que:
- 1- O lado CD é comum aos dois triângulos;
- 2- O ângulo formado pela altura é de 90 graus tanto para ACD quanto para BCD e
- 3- Os ângulos “f” e “g” são iguais pela propriedade anterior.
Os triângulos equiláteros
É importante lembrar que o triângulo equilátero recebe esse nome por que possui 3 lados iguais. Sendo assim, note que todo triângulo equilátero é também isósceles. Isso por que, olhando apenas dois de seus lados e ignorando o terceiro, observa-se um triângulo isósceles. Dessa forma, as duas propriedades acima são válidas para o triângulo equilátero assim como para o triângulo isósceles.
A novidade é que todos os ângulos de um triângulo equilátero são iguais e medem 60 graus. Os ângulos são iguais por que os lados são iguais. O valor deles é 60 graus por que a soma dos ângulos internos de um triângulo é 180 graus.
O Triângulo Retângulo
A importância do Triângulo REtângulo está nas relações trigonométricas nele estabelecidas., E que são a base para todo um desenvolvimento da matemática.
Confira agora as propriedades do Triângulo Retângulo e o Teorema de Pitágoras:
Veja 10 dicas sobre o Triângulo Retângulo:
- Esse triângulo se chama retângulo porque tem um ângulo reto (90º).
- O lado que estiver diante do ângulo reto será a hipotenusa.
- E os lados que formam o ângulo reto são chamados de catetos.
- Quando resolvemos problemas sobre triângulo retângulo você trabalhar com lados e medidas de segmentos. De todas as relações métricas que existem, o Teorema de Pitágoras é o mais recorrente nos vestibulares.
- O Teorema de Pitágoras diz que o quadrado da hipotenusa deve ser igual à soma do quadrado dos catetos: hip² = cat² + cat².
- Além desse teorema, podemos destacar outras relações métricas que se você souber vão facilitar muito a resolução do exercício:
- a) Existe uma relação que diz que o produto dos catetos é sempre igual ao produto da hipotenusa pela altura: cat.cat = hip.alt.
- b) Outra relação que você vai aprender na aula acima: todo cateto ao quadrado é igual ao produto da sua projeção pela hipotenusa: cat² = proj.hip.
- c) E, ainda mais essa relação: o quadrado da altura é igual ao produto das suas projeções: alt² = proj.proj.
- Confira com o professor Sarkis, porque todo ano cai.
Lista de Exercícios sobre a Classificação dos Triângulos
