Quadrilátero é um polígono de quatro lados. Quando possui lados opostos paralelos é chamados de paralelogramo. Já quando um par de lados opostos não é paralelo, é chamado de trapézio. Saiba mais nesta aula de Matemática para o Enem e o Encceja!
Você já conhece os quadriláteros paralelogramos no dia a dia. Eles estão por todo lado: nas mesas retangulares ou quadradas, nos campos de futebol, nas quadras de vôlei ou nos quadros utilizados por professores. Nesta aula você vai entender as características de um quadrilátero e a classificação em paralelogramos e trapézios.
O que é um quadrilátero
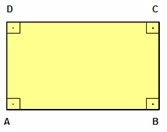
Quadrilátero é um polígono de quatro lados. A soma dos seus ângulos internos é igual a 360º, bem como dos ângulos externos. No quadrilátero ABCD da figura abaixo, destacam-se os seguintes elementos:
- Os pontos A, B, C e D são os vértices do quadrilátero ABCD.
- Os segmentos AB, BC, CD e DA são os lados do quadrilátero ABCD.
- Os ângulos Aˆ , Bˆ , Cˆ e Dˆ assinalados na figura são os ângulos internos do quadrilátero ABCD.
- O segmento AC, cujas extremidades são dois vértices não consecutivos, é uma diagonal do quadrilátero ABCD. O segmento BD é outra diagonal desse quadrilátero. Todo quadrilátero possui duas diagonais (iguais ou diferentes).
Os quadriláteros podem ser divididos em dois grupos: os quadriláteros paralelogramos e os trapézios. Em seguida veremos um pouco mais sobre cada um deles.
Quadriláteros paralelogramos
Paralelogramos são os quadriláteros que possuem lados iguais e paralelos dois a dois. Neste grupo estão o paralelogramo propriamente dito, o retângulo, o losango e o quadrado. Isso quer dizer que todo paralelogramo é um quadrilátero, mas nem todo quadrilátero é um paralelogramo.
Retângulo
O retângulo é o paralelogramo que tem os quatro ângulos congruentes, ou seja, os quatro ângulos são retos.
 Relações do retângulo:
Relações do retângulo:
- AB = CD e AD = BC
- As diagonais AC e BD são iguais.
Losango
O losango é o quadrilátero paralelogramo que tem os quatro lados congruentes. Seus ângulos opostos são congruentes sendo dois agudos e dois obtusos.
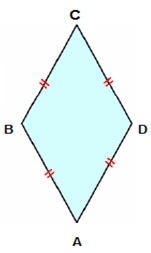
Relações do losango:
- AB = BC = CD = DA
- A diagonal AC é maior que a diagonal BD.
- As diagonais são perpendiculares.
- ^A = ^C e ^B = ^D
- ^A + ^B = 180º
Quadrado
O quadrado é o paralelogramo que tem os quatro lados congruentes e também os quatro ângulos congruentes (retos).
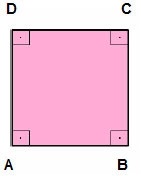
Relações do Quadrado:
- AB = BC = CD = DA
- A diagonal AC é igual a diagonal BD.
- As diagonais são perpendiculares.
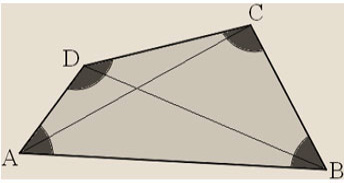
Paralelogramo
O paralelogramo propriamente dito é o quadrilátero que tem os lados opostos paralelos e iguais dois a dois.
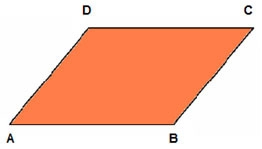
Relações do paralelogramo:
- ^ A = ^ C e ^ B = ^ D (os ângulos opostos são congruentes) e A + D = 180º e B + C = 180º.
- A diagonal AC é maior que a diagonal BD.
Trapézios
Trapézios são os quadriláteros que possuem apenas dois lados paralelos (denominados bases maior e menor). Os trapézios podem ser classificados em:
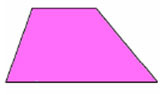
a) Escaleno: os lados oblíquos são diferentes.
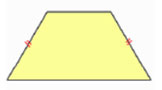
b) Isósceles: os lados oblíquos são iguais.
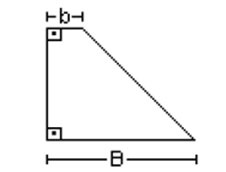
c) Retângulo: um dos lados oblíquos é perpendicular às bases.
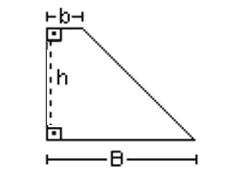
Propriedades de um trapézio
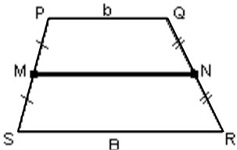
1) Num trapézio, as bases são os lados paralelos e a altura é a distância entre as bases.
2) Um trapézio retângulo tem dois ângulos internos retos e um dos lados perpendicular às bases.
3) Num trapézio isósceles, dois de seus lados opostos são congruentes e os ângulos das bases são iguais.
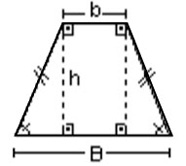
4) A base média de um trapézio é a média aritmética entre suas bases maior e menor.
Geometria plana
Saiba mais sobre quadriláteros paralelogramos e outras figuras planas nesta aula do canal Curso Enem Gratuito:
Exercícios sobre quadriláteros paralelogramos e trapézios
1 – (UFGD MS/2020)
Considerando os pontos A = (1,2), B = (4, –1), C = (2,–2) e D = (0,0), no plano cartesiano, é correto afirmar que o quadrilátero convexo com vértices nos pontos A, B, C e D é um
a) paralelogramo.
b) trapézio isósceles.
c) trapézio escaleno.
d) losango.
e) trapézio retângulo.
2 – (Unifenas MG/2020)
Sabe-se que um paralelogramo é um quadrilátero com lados opostos paralelos e congruentes. Considere que as medidas de seus ângulos sejam proporcionais a 1:5. Qual é a medida do elemento de seu menor ângulo?
a) 210º.
b) 250º.
c) 290º.
d) 310º.
e) 330º.
3 – (Encceja/2019)
Roger Penrose, professor na Universidade de Oxford e especialista mundial em relatividade e teoria quântica, descobriu um belíssimo tipo de pavimentação aperiódica, constituída apenas por dois tipos de ladrilhos, como se observa na figura 1.
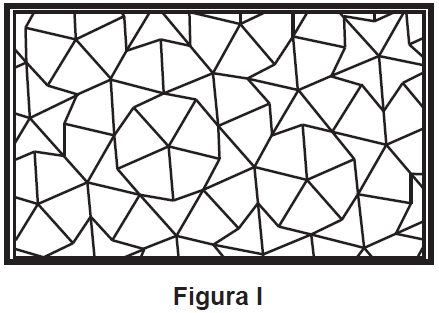
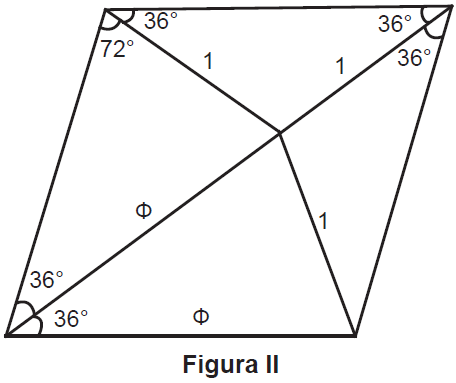
Esses dois tipos de ladrilhos, pelos seus aspectos, foram batizados de “flechas” e “papagaios” por John Conway (outro entusiasta de diversões matemáticas, à semelhança de Penrose). As “flechas” e os “papagaios” podem ser obtidos pela fragmentação de um polígono, como mostra a figura 2.
 Disponível em: www.educ.fc.ul.pt. Acesso em: 15 dez. 2012 (adaptado).
Disponível em: www.educ.fc.ul.pt. Acesso em: 15 dez. 2012 (adaptado).
Esse polígono é um
a) trapézio.
b) triângulo.
c) octógono.
d) paralelogramo.
4 – (UFJF MG/2015)
Dadas as seguintes afirmações:
I. Se um paralelogramo tem dois ângulos de vértices consecutivos congruentes, então ele é um retângulo.
II. A altura de um trapézio retângulo que tem o ângulo agudo medindo 30º é igual à metade do lado não perpendicular às bases.
III. Se as diagonais de um quadrilátero são congruentes e perpendiculares, então elas são bissetrizes dos ângulos desse quadrilátero.
É CORRETO afirmar que:
a) Apenas I é verdadeira.
b) Apenas II é verdadeira.
c) Todas as afirmações são verdadeiras.
d) Apenas I e II são verdadeiras.
e) Apenas II e III são verdadeiras.
5 – (UDESC SC/2013)
Considere num sistema de coordenadas cartesianas o polígono com vértices nos pontos A(–3, –3), B(3, 1), C(–3, 3) e D(–1, –1). O quadrilátero determinado pelos pontos médios dos segmentos AB, BC, CD e DA, nesta ordem, é um:
a) losango
b) retângulo
c) trapézio
d) quadrado
e) paralelogramo
Gabarito:
- B
- E
- D
- D