Ângulo Central e Ângulo Inscrito: Relembre tudo sobre Ângulos na Circunferência em mais esta aula preparatória para Matemática Enem e Vestibular. Resumo com as características do Círculo e da Circunferência. Aprenda agora como resolver os problemas.
Se você não lembra mais das aulas sobre as definições e os cálculos envolvendo os Ângulos na Circunferência, a hora é esta. Veja abaixo aula gratuita de revisão.
Vamos começar pelo começo. Você lembra a definição de circunferência ? Vamos lá: Circunferência é a linha fechada que contorna uma região chamada círculo.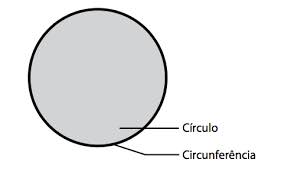 
Sim, simples assim, para nunca mais esquecer: a circunferência é a linha que demarca o círculo, como na imagem acima.
A diferença entre Círculo e Circunferência:
- O Círculo: Para você diferenciar claramente a circunferência (a linha que demarca) o círculo (o disco), perceba na imagem acima que o Círculo “é a reunião da circunferência com o conjunto de pontos localizados dentro da mesma”.
- Se ficou complicado de entender, volte na imagem com calma e observe novamente:
- A Circunferência é a linha preta que envolve a região cinza, enquanto o círculo é toda a região pintada de cinza reunida com a circunferência.
Os ângulos na circunferência
Para começar bem o seu resumo sobre os ângulos na circunferência acompanhe esta introdução completa com o professor Lucas Borguesan, do canal do Curso Enem Gratuito. Depois tem o segundo vídeo, com o complemento.
Confira a Aula 1
As dicas do Professor Lucas:
- Podemos dizer que todo polígono regular pode ser inscrito ou circunscrito a uma circunferência. Isso quer dizer que em todo polígono regular podemos “desenhar” uma circunferência no seu interior e no seu exterior.
- Caso a circunferência esteja no interior do polígono, dizemos que a circunferência está inscrita ao polígono ou que o polígono está circunscrito à circunferência.
- Por outro lado, caso a circunferência esteja no exterior do polígono, dizemos que a circunferência está circunscrita ao polígono ou que o polígono está inscrito à circunferência.
- Nesta aula acima, o professor Lucas vai te introduzir nos cálculos de ângulos da circunferência.
Os tipos de ângulos mais importantes na circunferência.
Ângulo central – Ângulo central (α) é o ângulo formado a partir do centro O. Observe a figura abaixo: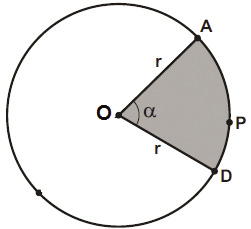
A medida do ângulo central α é igual à medida do arco APD. Por Exemplo: Se a medida do arco APD for igual a 60º, dizemos que a medida do ângulo central α vale também 60º.
Ângulo inscrito na circunferência
O Ângulo inscrito na circunferência (β) é o ângulo formado a partir do arco mas com vértice sobre a circunferência.Seu valor corresponde à metade do ângulo central (α).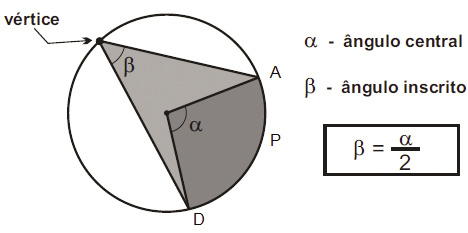
Os Ângulos na Circunferência – Aula 2
Valeu pra você este complemento do resumo do professor Lucas? De certeza que sim. Agora, vamos ver mais exemplos, e praticar.
Exemplo de ângulo inscrito na circunferência:
Sendo a medida do arco ABC igual a 110º , determine o valor dos ângulos x e y, conforme a figura abaixo: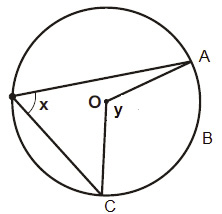
- Solução:Observe que a medida do arco é 110º e que o ângulo y representa a medida do ângulo central, ou seja, y = arco = 110º.
- O ângulo x da figura representa o ângulo inscrito na circunferência proveniente do mesmo arco que y, logo x vale a metade de y, ou seja, 55º.
- Resposta:x = 55º e y = 110º
Algumas consequências do ângulo inscrito
-
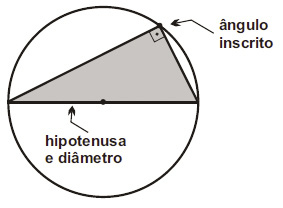
- 1. Todo triângulo retângulo pode ser inscrito numa semicircunferência, onde a hipotenusa coincide com o diâmetro.
- 1. Todo triângulo retângulo pode ser inscrito numa semicircunferência, onde a hipotenusa coincide com o diâmetro.
-
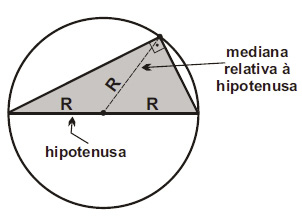
- 2. Em todo triângulo retângulo, a mediana relativa à hipotenusa vale a metade dessa hipotenusa.
- 2. Em todo triângulo retângulo, a mediana relativa à hipotenusa vale a metade dessa hipotenusa.
-
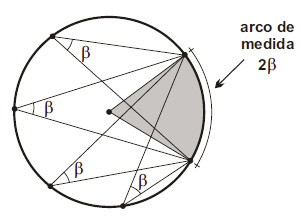
- 3. Todos os ângulos de uma circunferência inscritos no mesmo arco são congruentes.
- 3. Todos os ângulos de uma circunferência inscritos no mesmo arco são congruentes.
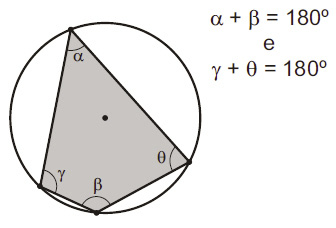
- 4. Em todo quadrilátero inscrito numa circunferência, os ângulos internos opostos são suplementares (somados valem 180º).
Veja O Círculo Trigonométrico
Quando falamos em seno, cosseno e tangente, tem quem até se arrepia! Todavia, a matéria é mais simples do que parece e ainda por cima é figurinha carimbada no Enem e nos vestibulares. Aqui, vamos simplificar o círculo trigonométrico para você!
Para compreender e desvendar os segredos da trigonometria, o primeiro passo é entender o ciclo trigonométrico. Veja com o professor Lucas Borghesan, do canal do Curso Enem Gratuito, as dicas do CírculoTrigonométrico:
Observe a imagem, e tente recuperar os conteúdos relacionados que você já estudou antes de prosseguir na leitura.
É um bom exercício para você refrescar a memória, lembrar o que sabe, e recuperar as dúvidas também.
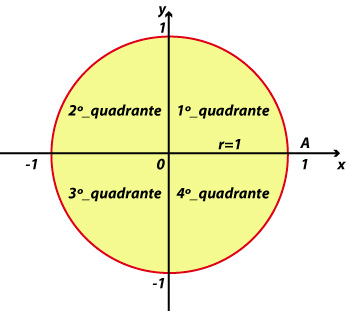Então quando formamos qualquer ângulo a partir da origem, surgem dois vetores, um no eixo das abscissas, e outro no das ordenadas, assim formando no eixo X os cossenos, e no eixo Y o seno, os quais possuem um valor entre 0 e 1, e a tangente é um valor formado prolongando o vetor do ângulo até uma reta tangente à circunferência.
Assim, forma-se um terceiro vetor chamado de tangente, de varia de 0 até tendendo a +/- infinito.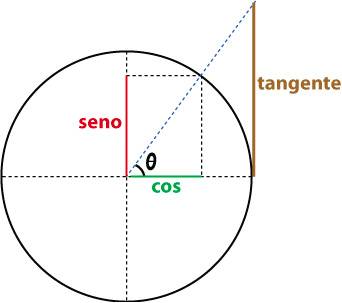 
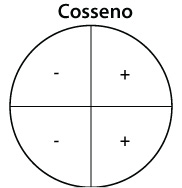
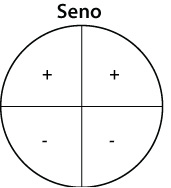
Seno e Cosseno:
Os sinais de seno, cosseno e tangente são respectivamente:
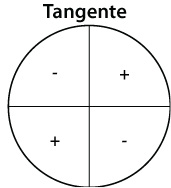
Veja as Relações do Círculo Trigonométrico
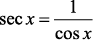
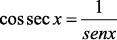
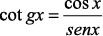
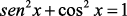
Exercício Resolvido de Trigonometria
O valor de y = cos 150° + sen 300° – tg 225° – cos 90° é
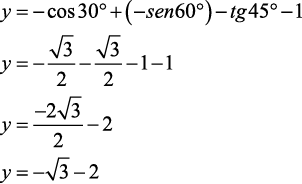
Sendo sen x = – 4/5 e 3π/2 < x < 2π, então a tg x é igual a
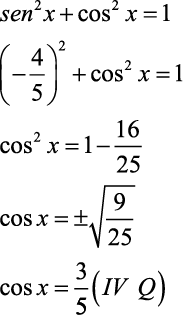
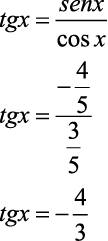
A origem da Trigonometria
Confira agora com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito, como você pode resolver as questões de Ângulos na prova de matemática do Enem.
Confira no vídeo acima estratégias para gabaritar tanto na geometria quanto na trigonometria com a resolução de problemas relacionados aos ângulos. Você vai entender o que é um ângulo, como pode medi-lo e, claro, tem resolução de problemas também.
Desafios para você resolver e compartilhar a solução nas redes sociais
Questão 01
Na circunferência abaixo, pode-se afirmar que: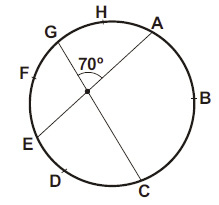
a) as medidas dos arcos AHG e EDG são iguais.
b) a soma dos arcos AHG e ABC é 180º.
c) a soma dos arcos GFE e ABC é 140º.
d) o arco GFE é maior que o arco EDC.
e) a soma dos arcos GFE e ABC é 220º.
Dica 1 – Você sabe a diferença entre um círculo e uma circunferência? Nesta aula de Matemática Enem você pode revisar tudo sobre essas duas formas geométricas – https://blogdoenem.com.br/circulo-e-circunferencia-matematica-enem/
Questão 02
Na figura abaixo, os pontos A, B e C são pontos da circunferência de centro O. O valor de x + y é: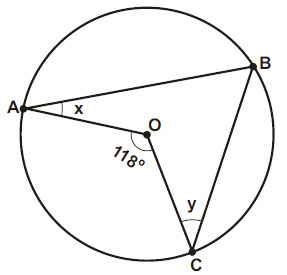
a) 242º
b) 121º
c) 118º
d) 59º
e) 62º
Dica 2 – Estude sobre Circunferência em mais esta aula de revisão para Matemática Enem. O Exame Nacional do Ensino Médio está chegando, estude com a gente! – https://blogdoenem.com.br/circunferencia-matematica-enem/
Questão 03
Determine o valor do ângulo x, conforme a figura abaixo:
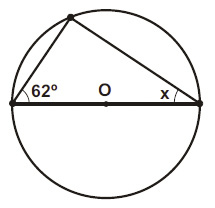
a) 24º; b) 28º; c) 38º; d) 17º; e) 32º
Dica 3 – Preparado para o Exame Nacional do Ensino Médio? Revise tudo sobre Geometria Analítica em mais uma aula de Matemática Enem que preparamos para você – https://blogdoenem.com.br/geometria-analitica-matematica-enem/
Questão 04
Determine o valor do ângulo x, conforme a figura abaixo: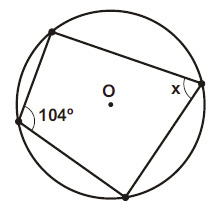
a) 70º; b) 76º; c) 80º; d) 82º; e) 85º
Questão 05
Na figura abaixo, AB é o diâmetro da circunferência de centro O. Determine a medida do ângulo ADC, sabendo que o ângulo BAC mede 35º.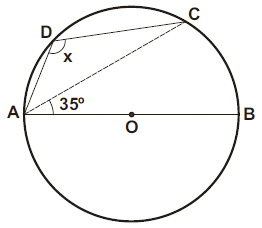
a) 150º; b) 176º; c) 125º; d) 182º; e) 105º
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
