Nesta aula você poderá estudar o conceito de uma função, seu estudo no plano cartesiano assim como interpretar, analisar e construir uma função graficamente. Que tal esse tema para complementar e aprofundar seus estudos em matemática para o Enem?
Matemática Enem: Em diversas situações do dia a dia é possível perceber grandezas que, de certa maneira, estão relacionadas. Ao abastecer um veículo, por exemplo, as grandezas “quantidade de combustível” e “quantia a pagar” estão diretamente relacionadas. Muitas destas relações podem ser descritas por um conceito matemático denominado função, e com representação gráfica num Plano Cartesiano.
O Plano Cartesiano
Ao relacionarmos espaço em função do tempo, número do sapato em função do tamanho dos pés, intensidade da fotossíntese realizada por uma planta em função da intensidade de luz a que ela é exposta ou pessoa em função da impressão digital.
Também é possível relacionar os lucros e investimentos de uma empresa, horas de funcionamento de uma máquina e consumo de energia percebemos quão importantes são os conceitos de funções para compreendermos as relações entre os fenômenos físicos, biológicos, sociais.
Veja na imagem como se representa uma função num Plano Cartesiano: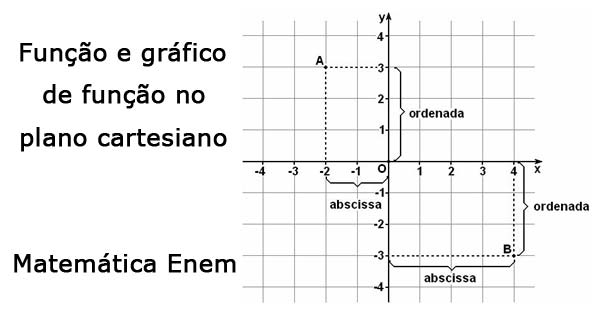
Entenda o Plano Cartesiano
O plano cartesiano ortogonal é constituído por dois eixos x e y perpendiculares entre si que se cruzam na origem. O eixo horizontal é o eixo das abscissas (eixo OX) e o eixo vertical é o eixo das ordenadas (eixo OY). Associando a cada um dos eixos o conjunto de todos os números reais, obtém-se o plano cartesiano ortogonal.
Cada ponto P = (a,b) do plano cartesiano é formado por um par ordenado de números, indicados entre parênteses, a abscissa e a ordenada respectivamente. Este par ordenado representa as coordenadas de um ponto.
O ponto “O” equivalente ao número zero, é a origem do plano cartesiano, ou seja, o cruzamento dos eixos.
Representação dos pontos A e B:

O Produto Cartesiano
Veja agora uma introdução ao Produto Cartesiano com o professor Lucas, do canal do Curso Enem Gratuito. Ele vai ajudar você a compreender o que é uma função e também as representações gráficas delas.
Então, agora, depois desta super aula, fica mais tranquilo de você prosseguir. Vamos lá:
Dados dois conjuntos A e B não vazios, denominamos o produto cartesiano entre A e B, denotado por A x B (lê-se: A cartesiano B ou produto cartesiano A por B), como o conjunto de todos os pares ordenados da forma (x,y) onde x pertence ao primeiro conjunto A e y pertence ao segundo conjunto B.

Relações de “R” de “A” em “B “

Veja as diferentes formas de representação:
Conjuntos: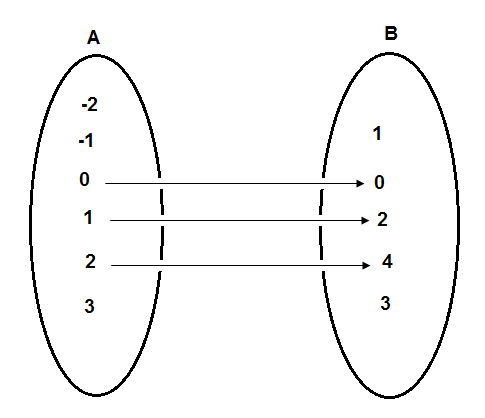
Agora, a representação num Plano Cartesiano: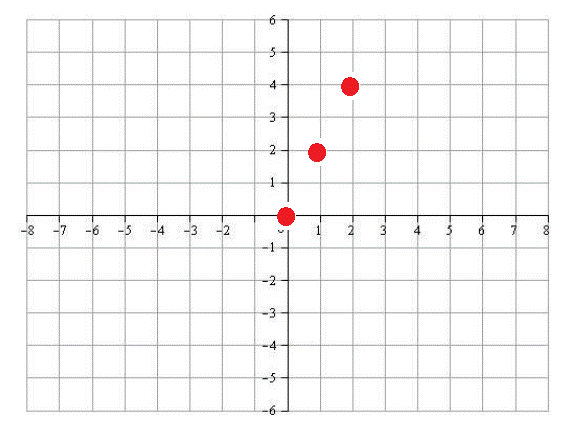
Conceito de Função (noção intuitiva de função)
O conceito de função é um dos mais importantes da matemática. Ele está sempre presente na relação entre duas grandezas variáveis. Assim são exemplos de funções:
- – O valor a ser pago numa corrida de táxi é função do espaço percorrido;
- – A área de um quadrado é função da medida do seu lado;
- – Em um termômetro, a temperatura é dada em função do comprimento da coluna de mercúrio.
Definição:

Exemplos:a) 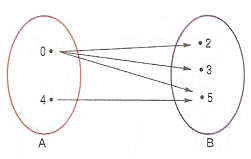
Não é função, pois o elemento 0 de A está associado a 3 elementos de B.b) 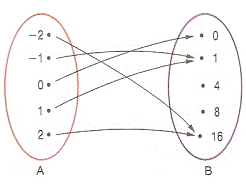
É função, pois todos os elementos de A estão associados a um único elemento de B.c) 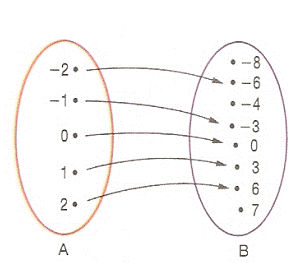
É função, pois todos os elementos de A estão associados a um único elemento de B.d) 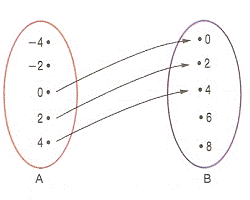
Não é função, pois os elementos -2 e -4 de A não estão associados a algum elemento de B.
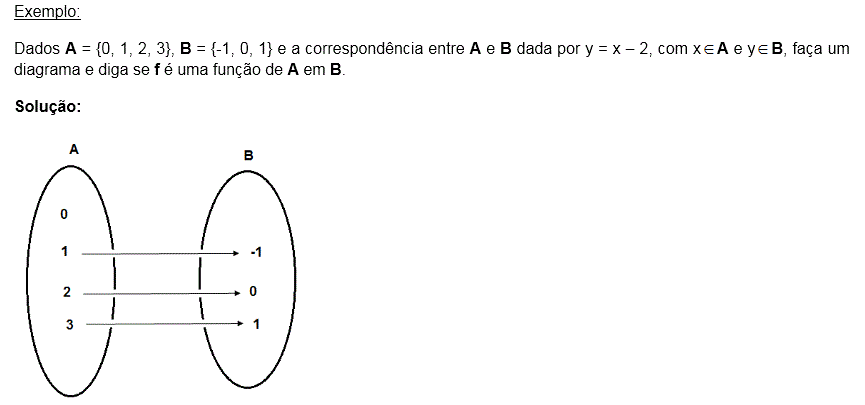
Não é função, pois o elemento 0 de A não está associado a algum elemento de B.
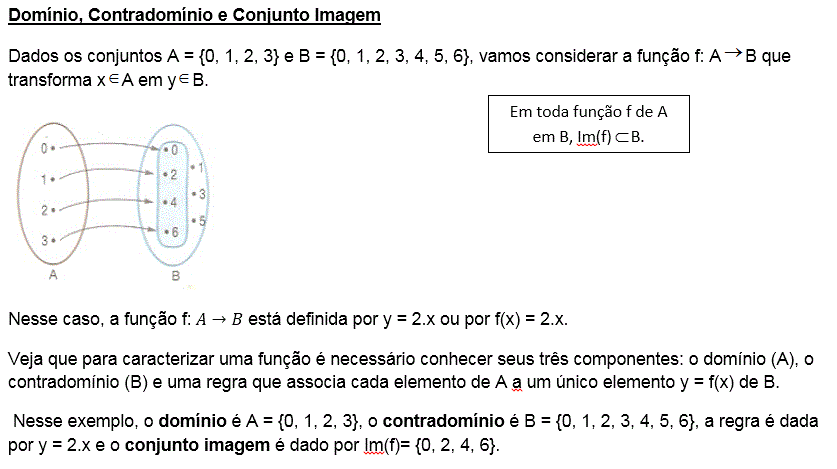

Valor numérico de uma função
Para calcular o valor numérico de uma função qualquer num ponto dado, basta substituir este ponto pela variável x na função dada.

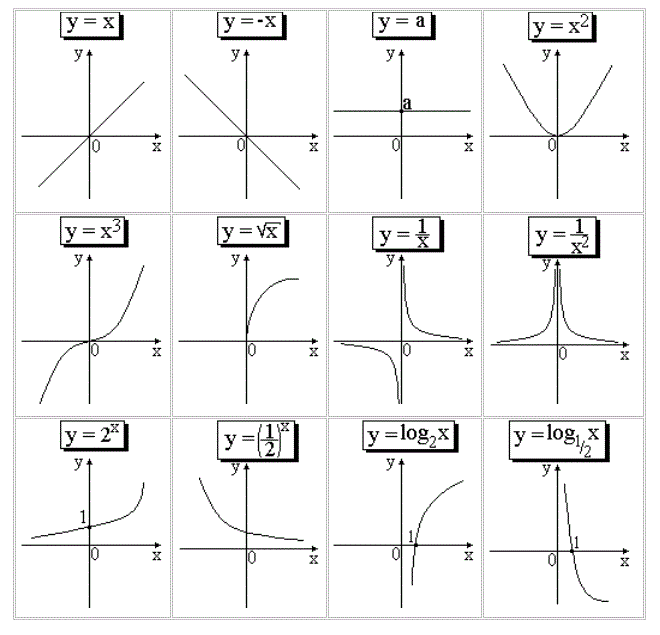
Gráficos Fundamentais para entender o Plano Cartesiano:
Exercícios

Os textos e exemplos acima sobre Função e Plano Cartesiano foram preparados pela professora Jaceli Eccher para o Blog do Enem. Jaceli é formada em Matemática habilitação Licenciatura pela Universidade Federal de Santa Catarina com Especialização no ensino de Ciências pelo Instituto Federal de Santa Caratina. Facebook: https://www.facebook.com/Jacelieccher

