Que tal começar a perder o medo da prova de matemática do Enem a partir de agora? Hoje vou mostrar alguns caminhos bastante práticos para você entender as funções algébricas de 1º grau,e aprender a resolver as questões. Todo ano cai!
Tá com medo, ou sente arrepior só de pensar na prova de Matemática? Bora virar esse jogo! Se tem algo que eu percebi ao estudar Matemática ao longo da minha vida é que você precisa entender para gostar do assunto. E por melhor que seja o professor, esse aprendizado só depende de você. Hoje é o dia para dominar as As funções algébricas do 1˚ grau.
Então, tente esquecer todas as vezes que você não conseguiu aprender essa matéria. Encare os cálculos matemáticos como um jogo, um quebra-cabeça. Imagine que o seu desafio é encontrar um resultado.
Tem coisa que a gente nunca aprende só porque nunca tentou, de verdade, encarar e ver como é. Portanto, aproveite que você chegou até aqui e marque na sua agenda: Nesta data eu entendi p que são, e aprendi como calcular , e como resolver as questões de funções algébricas do 1˚ grau. Então, agora vamos lá!
As Funções Algébricas do 1º Grau
“Uma função que possa ser obtida por um número finito de operações algébricas”. Assim é definida uma função algébrica. Elas podem aplicadas em cálculos de Engenharia, Física, Economia e até em Música.
Ainda está complicado? Então, vamos pegar aqui cinco minutos com o professor Lucas Borguesan, do Curso Enem Gratuito, para você perder o medo de encarar as funções algébricas do 1˚ grau.
Acompanhe com o professor Lucas, e veja como dá sim pra encarar e vencer na Matemáica do Enem, dos vestibulares, ou do Encceja.
As dicas do professor Lucas:
- As funções algébricas do 1˚ grau são bem exploradas nos vestibulares e no Enem. Ela é apresentada de diversas formas e inserida em diversos assuntos.
- Caem Funções nas questões de Estatística, Matemática Financeira, e em várias situações problemas em outras áreas de conhecimento como Física, Biologia e Geografia.
- Nesta aula, o professor Lucas te ensina os conceitos de Funções e ainda te dá dicas de como resolver sem dificuldade os problemas matemáticos com funções.
- Veja os principais tópicos:
- A – O que é Função.
- B – Qual a diferença de Função para outras operações ;
- C – Qual a utilidade das funções?
- D – Exercícios Resolvidos de Funções algébricas do Primeiro Grau.
- Confira no vídeo acima, pois você vai perder o medo e mandar muito bem nas próximas provas.
Exemplo de funções algébricas do 1˚ grau:
Veja aqui um exemplo bem prático, de como as funções de primeiro grau estão presentes no seu dia a dia. Observe no exemplo uso das Funções para fazer um cálculo0 básico de Economia. Você vai fazer as contas através da Função Receita, Função Custo e Função Lucro, onde:
- Função Custo é igual ao custo fixo mais o custo variável (que depende de unidades vendidas, por exemplo). Veja na representação, e na explicação:
- C(x) = Cf+C(x)
- Função Receita é igual ao preço vezes a quantidade vendida: R(x)=P.x
Função Lucro é igual à Receita Total menos o Custo Total: L(x)=R(x) – C(x)
Preste atenção no exemplo:
O custo de produção de determinado produto tem um custo fixo de R$ 30,00, onde estão inclusos salários, impostos, água e energia elétrica, mais um custo variável de R$ 5,00 por cada peça produzida. O preço de venda de cada peça é R$ 80,00. Determine então o lucro obtido com a venda de 50 unidades.
Função Custo: C(x) = 30 + 5x
Função Receita: R(x) = 80x
Função Lucro: L(x) = R(x) – C(x)
L(x) = 80x – (30 + 5x)
L(x) = (80x – 5x)- 30
L(x) = 75x – 30
Agora precisamos saber o lucro de 50 unidades, certo? So substituir o X por 50. Vamos lá.
L(x) = (75 x 50) – 30
L(x) = 3.720,00
Este é então, um exemplo do uso de funções em Economia.
Dica 1: que tal revisar o conceito de funções? https://blogdoenem.com.br/funcoes-matematica-enem-vestibular/
Exemplo de funções algébricas do 1˚ grau
O que caracteriza uma função do 1º grau?
1. Trabalha-se com expressões algébricas do tipo (ax+b), de onde vem a função f(x)= ax + b. Essa função é também conhecida como função afim.
2. O objetivo da função é relacionar para cada valor de x um valor para o f(x).
3. As expressões f(x) = ax + b e y= ax + b, são iguais? Acertou quem respondeu sim, já que em matemática f(x) e y são a mesma coisa.
4. Outra dica muito importante: o gráfico de uma função de 1º grau é sempre um reta. Quando o a for positivo, teremos uma reta crescente e com o a negativo, uma reta decrescente.
5. Nas expressão das funções algébricas do 1˚ grau, o a e o b devem ser números reais e o a tem que ser diferente de zero.
Vamos à parte prática
Observe a expressão: y = 2x + 3
Passo 1:
Separar os valores: a= 2 e b=3.
Passo 2:
Dar valores ao x (esses valores podem ser qualquer número, a dica é que se escolha um número baixo, como 1, 2, por exemplo).
Passo 3:
Calcular a expressão utilizando os valores escolhidos para x. Nesse caso, vamos usar os valores 1 e 2. Observe:
y = 2(1) + 3
y = 2 + 3
y = 5 (ou f(x) = 5)
e
y = 2(2) + 3
y = 4 + 3
y = 7
Passo 4:
Identificar os pontos encontrados (x,y): (1,5) e (2, 7) –> são esses pontos que vão formar a reta.
Passo 5:
Montar o gráfico, marcar os pontos e ligar a reta. Lembre-se de que x é a linha horizontal e y a linha vertical.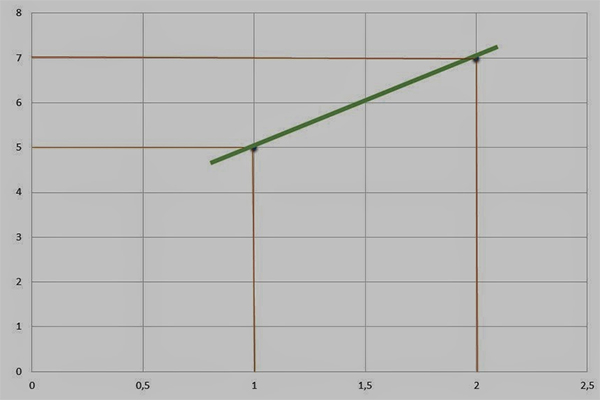
Pronto, a função está resolvida. Como você pode ver, não é tão difícil assim. Estudar matemática fica menos complicado quando começamos pelas operações mais simples.
Equações de Primeiro Grau
Veja agora um resumo sobre as Equações de Primeiro Grau, com o professor Sérgio Sarkis. É show!
Parabéns. Você chegou ao fim do resumo de um tema fundamental para mandar bem na Matemática do Enem. Agora, é com você para mandar bem nas provas. Bora lá!
Este post sobre as funções algébricas do 1˚ graufoi escrito por Elia Macedo. Ela estuda Ciências Contábeis na Unisinos, em Florianópolis e é apaixonada por Matemática. https://www.facebook.com/elia.macedo.



