Uma Função de 1º Grau se escreve assim y = f(x) = ax + b para determinar uma relação existente entre dois conjuntos. É um conteúdo básico da Matemática. Veja aula gratuita.
A ideia de Função de 1º Grau, ou de Função Afim, surge pela primeira vez cerca de 2000 a.C. com os babilônios. Eles se valiam de tabelas como a descrita abaixo para associar a cada número natural seu quadrado.
Olhando hoje “parece simples”, mas foi uma descoberta e tanto para a história da Matemática.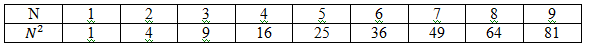
Três mil e quinhentos anos depois dos babilônios, agora na Itália, o astrônomo e inventor Galileu Galilei (1564 – 1642) mostrou que o espaço percorrido por um corpo em queda livre varia de acordo com o tempo gasto para percorrê-lo.
Entenda a Função de 1º Grau, ou Função Afim
Veja no exemplo bem prático no vídeo do professor Lucas Borguezan como a proposta de Galileu Galilei é válida até hoje para calcular o preço de uma corrida de Uber ou de Táxi. É uma conta simples de Função de primeiro grau, ou Função Afim:
Ou seja, da mesma forma que o professor Lucas Borguezan mostrou como se faz o cálculo de uma viagem de Uber, Galileu Galilei demostrou que o espaço percorrido é dado por uma função.
Para Galileu, o cálculo da Distância é feito em função do Tempo durante a queda, e da Aceleração da Gravidade (a aceleração da gravidade é de aproximadamente g = 9,8 m/s² ).
Agora que ficou mais fácil para você compreender as descobertas de Galileu Galilei. Veja com calma como é simples para fazer estas contas a partir da descoberta de Galileu.
Ele realizou experimentos soltando diversos corpos do alto de torres na Itália para descobrir os segredos do Movimetento em queda-livre, e entender porque a fórmula para calcular as variáveis é uma Função. Fonte
- – TODOS os corpos caem com a mesma aceleração da gravidade (g) e isso é uma propriedade do espaço;
- – A distância percorrida por um corpo em queda livre equivale o quadrado do tempo levado para percorrer essa distância;
- Sabemos que V = g . t
- Ou seja, dessa última conclusão temos a fórmula para calcular a distância percorrida por um corpo em queda livre:
d = distância percorrida (em metros);
g = 9,8 m/s² (aceleração da gravidade);
t = tempo gasto (em segundos).
Sem medo da Função de 1º Grau
Veja com o professor Lucas Borguesan uma tradução bem simples para você perder o medo na hora de resolver Função de Primeiro Grau nas provas do Enem, do Encceja, ou nos vestibulares.
Definição de Função de 1º Grau
Vamos simplificar para você entender melhor. Confira agora esta explicação de outra forma:
Função é uma relação entre dois conjuntos. Começaremos destacando a função polinomial de 1º grau mais simples, a função identidade, onde y = f(x) = x.
Além da estrutura mais geral da função de 1º grau, y = f(x) = ax + b, temos uma estrutura mais simples, do tipo y = f(x) = ax. Fonte
Resumo grátis com exercícios resolvidos de Funções
Muito bom este resumo com os exemplos. Vamos em frente.
Uma Função de 1º grau se escreve assim:
- f(x) = ax + b com a diferente de zero.
- Observe que a função é de primeiro grau, pois o expoente da variável x é o número 1.
- Na função acima, o número a é chamado de coeficiente de x , e o número b é chamado termo constante.
Veja os tipos de Funções de 1º grau
- a) Função Afim: f(x) = 5x – 15
- A Função Afim também conhecida como função polinomial de grau 1 ou função polinomial de primeiro grau cujo gráfico é uma reta não perpendicular ao eixo x .
- b) Função Linear: f(x) = -7x
- As funções lineares ocorrem quando o termo independente de x é igual a zero, isto é, quando
. - Neste caso particular a denominamos função linear.
- Assim sendo, toda função função linear pode ser representada assim:
- (fonte: Matemática Didática).
Bora simplificar: veja aula Gratuita com resumo rápido e fácil
O professor Sérgio Sarkis, do Curso Enem Gratuito, preparou uma aula prática com resolução de exercícios para você dominar geral a Função do Primeiro Grau. Confira:
Muito show este resumo. Simplifica geral e facilita para aprender.
Definição de Função
Sejam A e B dois conjuntos não-vazios. Uma função de A em B é uma relação f que a cada elemento de A associa um único elemento de B. Pela definição, representam funções os seguintes diagramas: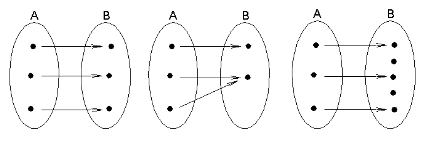
E não representam funções os seguintes (veja as imagens com calma para entender porque nesta figura abaixo não temos uma representação de funções):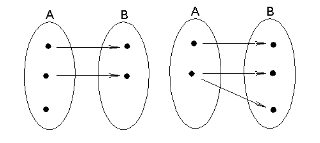
GRÁFICO DE UMA FUNÇÃO
Como Função de 1º Grau é uma relação em particular, devemos revisar a aula sobre relações no plano para entender melhor o gráfico de uma função. Nosso estudo esta direcionado às funções cujo domínio e o contradomínio são subconjuntos de ℝ, desta forma, podemos representar uma função num plano de ℝ×ℝ, como fazíamos com as relações.
O gráfico de uma função permite, entre outras coisas, a interpretação de relatórios, a indicação do preço de moedas, a análise de pesquisas estatísticas, etc.
Ao representar o gráfico de uma função, a variável independente é marcada sobre o eixo das abscissas (eixo horizontal) e a variável dependente sobre o eixo das ordenadas (eixo vertical).
DEFINIÇÃO
Seja uma função. O gráfico de f é o conjunto de todos os pontos (x, f(x)), do plano cartesiano tais que e onde x pertence ao eixo horizontal e f(x) pertence ao eixo vertical. Observe o gráfico abaixo: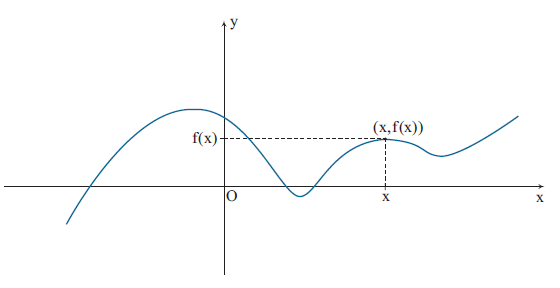
Veja o gráfico desta outra função
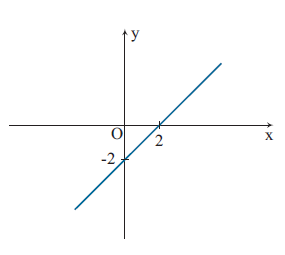
Exercício Resolvido de Função de 1º Grau
(Enem 2010): As sacolas plásticas sujam florestas, rios e oceanos e quase sempre acabam matando por asfixia peixes, baleias e outros animais aquáticos. No Brasil, em 2007, foram consumidas 18 bilhões de sacolas plásticas.
Os supermercados brasileiros se preparam para acabar com as sacolas plásticas até 2016. Observe o gráfico a seguir, em que se considera a origem como o ano de 2007.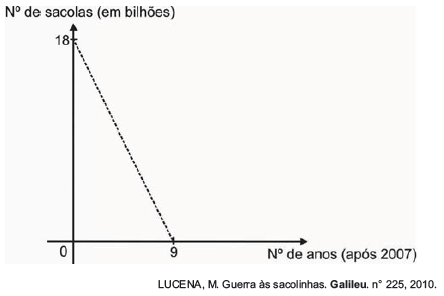
De acordo com as informações, quantos bilhões de sacolas plásticas serão consumidas em 2011?
a) 4,0
b) 6,5
c) 7,0
d) 8,0
e) 10
Resolução: Para encontrar o valor pedido, devemos primeiro achar a função. Analisando o gráfico acima, vemos que os pontos (0, 18) e (9, 0) fazem parte do gráfico da função, ou seja, quando temos que: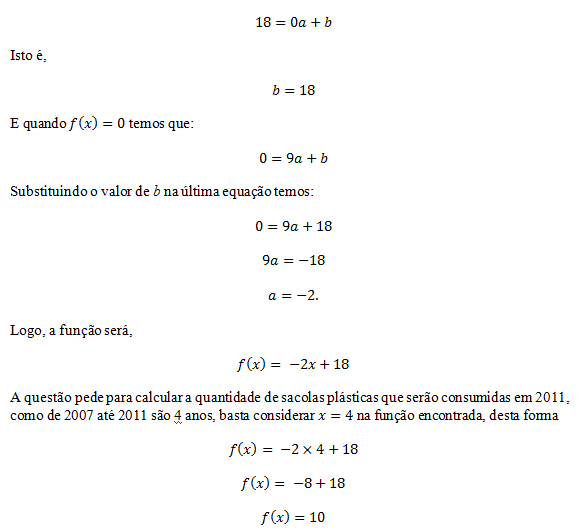
Logo, a resposta certa corresponde à alternativa E.
Função do Primeiro Grau
.
