Entender e relacionar diferentes grandezas faz parte das competências do Enem. Aprenda a relacionar volume, massa, superfície, comprimento, capacidade, velocidade, tempo, e até o custo da produção para colocar o cérebro soltando faisca!
A quarta competência exigida na prova do Exame Nacional do Ensino Médio (Enem) pede que o aluno relacione grandezas de diferentes formas.
É essa competência que testa os conhecimentos sobre grandeza diretamente proporcional (quanto o aumento do valor a ser pago aumenta o número de caixas de leite compradas no mercado, por exemplo) e a ‘inversamente proporcional’ (quanto diminui o tempo de percurso de um caminho quando você aumenta a velocidade).
Resumo de Grandezas Escalares e Vetoriais
Grandezas: aquilo que pode ser medido, contado
Entendemos por grandeza tudo aquilo que pode ser medido, contado. As grandezas podem ter suas medidas aumentadas ou diminuídas.
Alguns exemplos de grandeza: o volume, a massa, a superfície, o comprimento, a capacidade, a velocidade, o tempo, o custo e a produção. É comum ao nosso dia-a-dia situações em que relacionamos duas ou mais grandezas.
Por exemplo: Em uma corrida de “quilômetros contra o relógio”, quanto maior for a velocidade, menor será o tempo gasto nessa prova. Aqui as grandezas são a velocidade e o tempo.
Num forno utilizado para a produção de ferro fundido comum, quanto maior for o tempo de uso, maior será a produção de ferro. Nesse caso, as grandezas são o tempo e a produção.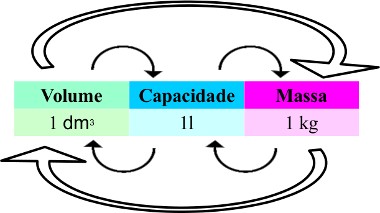
Grandezas diretamente proporcionais
São aquelas grandezas onde a variação de uma provoca a variação da outra numa mesma razão. Se uma dobra a outra dobra, se uma triplica a outra triplica, se uma é divida em duas partes iguais a outra também é divida à metade.
Exemplo 1 – Se três cadernos custam R$ 8,00, o preço de seis cadernos custará R$ 16,00. Observe que se dobramos o número de cadernos também dobramos o valor dos cadernos.
Confira pela tabela: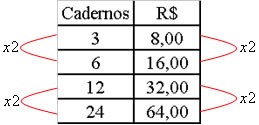
Grandezas inversamente proporcionais
Uma grandeza é inversamente proporcional quando operações inversas são utilizadas nas grandezas. Por exemplo, se dobramos uma das grandezas temos que dividir a outra por dois, se triplicamos uma delas devemos dividir a outra por três e assim sucessivamente.
A velocidade e o tempo são considerados grandezas inversas, pois aumentarmos a velocidade, o tempo é reduzido, e se diminuímos a velocidade, o tempo aumenta.
Exemplo 2 – Para encher um tanque são necessárias 30 vasilhas de 6 litros cada uma. Se forem usadas vasilhas de 3 litros cada, quantas serão necessárias?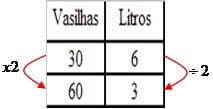
Utilizaremos 60 vasilhas, pois se a capacidade da vasilha diminui, o número de vasilhas aumenta no intuito de encher o tanque.
As duas grandezas são muito utilizadas em situações de comparação, isto é comum no cotidiano. A utilização da regra de três nos casos envolvendo proporcionalidade direta e inversa é de extrema importância para a obtenção dos resultados.
Propriedade: Em grandezas inversamente proporcionais, o produto é constante.
50 x 10 = 500 = 4 x 150 = 5 x 100 = K
Regra de três
Para resolver problemas relacionados às Grandezes é preciso dominar o mecanismo da regra de três, e saber fazer os cálculos envolvendo porcentagem e juros simples ou compostos.
Situações cotidianas, como juros cobrados por instituições bancárias ou o aumento do preço final de um produto quando resolvemos comprá-lo financiado são questões recorrentes no exame.
Venha conferir este resumo, as dicas e exercícios resolvidos para dar um show em matemática no Enem. Confira com o professor Sérgio Sarkis, do canal do Curso Enem gratuito:
O conhecimento e a utilização de conceitos semelhantes à regra de três são muito antigos, tendo sua provável origem na China antiga, podendo ser observados em tempos muito distantes.
Vários problemas envolvendo manipulações muito próximas do que hoje conhecemos como regra de três podem ser vistos no Papiro Rhind, documento confeccionado no Egito há cerca de 3000 anos. Mais recente que o Papiro Rhind, o livro Liber Abaci do matemático italiano Leonardo Fibonacci (1175-1250) revela vários problemas envolvendo a regra de três.
Apesar de sua criação ser tão remota, as aplicações relativas à regra de três são as mais variadas. Tratando da matemática utilitária, podemos dizer que a regra de três é primordial a nossa vida, pois soluciona questões corriqueiras com muita simplicidade e economia de tempo.
Veja o resumo rápido de Regra de Três com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito:
Regra de três simples
Quando, em uma relação entre duas grandezas, conhecemos três valores de um problema e desconhecemos apenas um, poderemos chegar a sua solução utilizando os princípios da regra de três simples. Para isso, basta que multipliquemos os meios entre si e os extremos também entre si. Acompanhem:
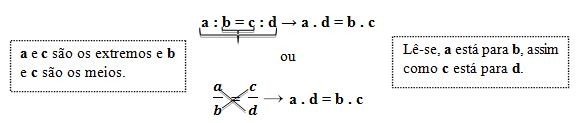
Exemplo: os números 6 e 10 são diretamente proporcionais a 12 e x respectivamente. Nessas condições, vamos encontrar o valor de x que torne essa afirmação verdadeira.
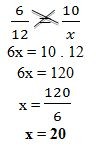
Regra de três composta
Quando trabalhamos com três grandezas, direta ou inversamente proporcionais e, num determinado problema, existem seis valores, dos quais cinco são conhecidos e apenas um desconhecido, pode-se encontrar o valor da incógnita através da regra de três composta.
Exemplo: Se 8 homens levam 12 dias montando 16 máquinas, então, nas mesmas condições, 15 homens levarão quantos dias para montar 50 máquinas?
● Vamos chamar o valor desconhecido de x e montar uma tabela contendo os valores:
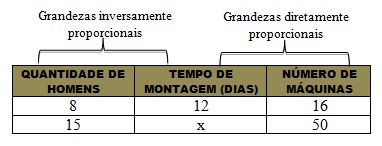
Analisemos as grandezas a fim de saber se são direta ou inversamente proporcionais entre si.
Fixando a grandeza quantidade de homens, vamos relacionar as grandezas tempo de montagem com número de máquinas. Se dobrarmos o tempo de montagem, dobraremos o número de máquinas. Logo, essas duas grandezas são diretamente proporcionais.
Fixando a grandeza número de máquinas, vamos relacionar as grandezas quantidade de homens com tempo de montagem. Se dobrarmos o número de homens, teremos reduzido à metade o tempo de montagem. Logo, essas duas grandezas são inversamente proporcionais.
Sabendo dessas informações, basta escrevermos a proporção de acordo com a tabela acima;
Como temos grandezas inversamente proporcionais, devemos inverter uma das frações;
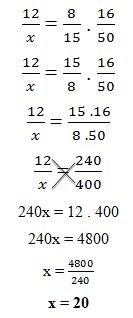
Conclusão: Com 15 homens, serão construídas 50 máquinas em 20 dias.
Resumo de Grandezas
Para finalizar bem a sua revisão veja este resumo rápido sobre as Grandezas Escalares e as Grandezas Vetoriais. Confira com o professor Marcos Rossetto, do canal do Curso Enem Gratuito:
Para finalizar bem a sua revisão veja este resumo rápido sobre as Grandezas Escalares e as Grandezas Vetoriais. Confira com o professor Marcos Rossetto, do canal do Curso Enem Gratuito:
Exercícios sobre as Grandezas
Exercício – 1 (ENEM) Uma escola lançou uma campanha para seus alunos arrecadarem, durante 30 dias, alimentos não perecíveis para doar a uma comunidade carente da região. Vinte alunos aceitaram a tarefa e nos primeiros 10 dias trabalharam 3 horas diárias, arrecadando 12 kg de alimentos por dia. Animados com os resultados, 30 novos alunos somaram-se ao grupo, e passaram a trabalhar 4 horas por dia nos di- as seguintes até o término da campanha. Admitindo-se que o ritmo de coleta tenha se mantido constante, a quantidade de alimentos arrecadados ao final do prazo estipulado seria de:
a)920kg
b)800kg
c)720kg
d)600kg
e)570kg
R: A
Exercício – 2 (UFG) Para encher um recipiente de 5 litros, uma torneira gasta 12 se- gundos. Uma segunda torneira gasta 18 segundos para encher o mesmo recipiente. Nestas condições, para encher um tanque de 1000 litros, usando as duas torneiras ao mesmo tempo, serão necessários, em minutos:
a) 20
b)24
c)33
d)50
e)83
R: B
Exercício – 3 (ESPM-SP) Em 10 minutos, 27 secretárias com a mesma habili- dade digitaram o equivalente a 324 páginas. Nas mesmas condições, se o número de secretárias fosse 50, em quantos minutos teorica- mente elas digitariam 600 páginas?
a) 10min
b) 45min
c) 5min
d) 5min e 24seg
e) 34min e 29seg
R: A
Curso Enem Gratuito
Quer aumentar suas chances no próximo Exame Nacional do Ensino Médio e mandar bem nas Notas de Corte do Enem? Estude com as apostilas e aulas gratuitas do Curso Enem Online. Todas as matérias do Exame e ainda as Dicas de Redação. Acesse aqui o Curso Enem Gratuito Online.
Acesse aqui os Aulões do Blog do Enem! São videoaulas gratuitas e completas com os conteúdos mais relevantes para o Exame Nacional do Ensino Médio.




