Entenda como funciona uma Lupa. Aprenda os segredos do comportamento da luz quando ela atravessa uma lente esférica. Veja agora, no resumo Enem Gratuito de Física:
Veja um resumo básico sobre as Lentes Esféricas, e depois responda aos desafios no final do post. É conteúdo clássico de Física para as provas do Exame Nacional do Ensino Médio.
Definimos lentes como sendo um sistema óptico formado por um meio homogêneo e transparente, limitado por duas superfícies esféricas ou por uma superfície esférica e outra plana.
O modelo mais popular de uma lente esférica é a Lupa, que você conhece. confira nesta imagem a seguir:

Agora, para você compreender como e porquê você consegue aumentar uma imagem utilizando a lupa, e como consegue achar “o foco” fazendo um movimento de aproximar ou de se afastar do objeto, confira no resumo do professor Diego, do canal do Curso Enem Gratuito:
Resumo sobre Lentes Esféricas:
As lentes são classificadas em dois tipos, as de bordas delgadas e as de bordas espessas.
Lentes de bordas delgadas

Lentes de bordas espessas:

Classificação de acordo com o índice de refração
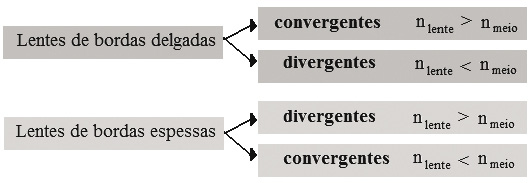
Podemos ainda classificar as lentes como sendo convergentes ou divergentes, de acordo com o índice de refração da lente. As lentes de bordas delgadas, quando possuem índice de refração maior que a do meio, são ditas convergentes; pelo contrário serão divergentes. Já as lentes de bordas espessas, quando possuem índice de refração maior que do meio, são ditas divergentes; pelo contrário serão convergentes.
Elementos de uma lente esférica
Devemos agora definir alguns elementos necessários para construir uma lentes esférica:
- centros de curvatura (C1, C2): centros das superfícies esféricas das faces da lente;
- vértices (V1, V2): polos das superfícies esféricas.
- focos (f1, f2): ponto situado entre o vértice e o centro de curvatura, e é calculado como metade do centro (f1,2= C1,2/2);
- eixo principal: a reta suporte que passa pelo centro de curvatura e pelo vértice da lente.
Raios notáveis
Vamos agora definir o caminho realizado pelos raios quando incidem sobre lentes convergentes e divergentes.
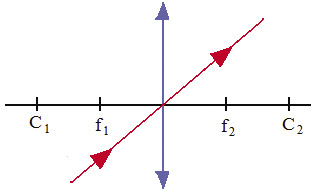
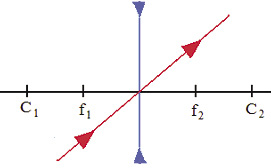
1º. Um raio de luz incidindo sobre o vértice:
- para lentes convergentes e divergentes, o raio de luz continua seu trajeto sem sofrer desvio;
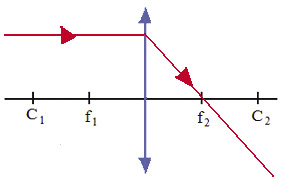
2º. Um raio de luz incidindo paralelo ao eixo principal:
- para uma lente convergente, atravessa a lente na direção do segundo foco;
- para uma lente divergente, atravessa a lente na onde o prolongamento do raio estará na direção do primeiro foco.
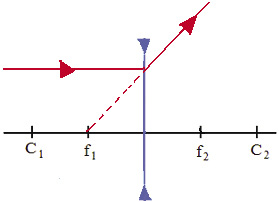
3º. Um raio de luz incidindo na lente passando pelo primeiro foco (caso convergente), ou incidindo na lente com o seu prolongamento passando pelo segundo foco (caso divergente):
- para uma lente convergente ou divergente, atravessa a lente na direção paralela ao eixo principal.
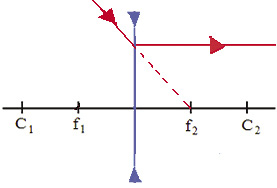
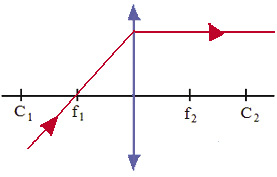
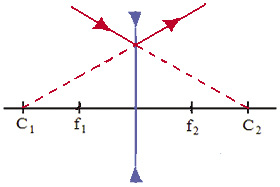
4º. Um raio de luz incidindo na lente passando pelo primeiro centro de curvatura (caso convergente), ou incidindo na lente na com seu prolongamento da direção passando pelo segundo centro de curvatura (caso divergente):
- para uma lente convergente, o raio atravessa a lente em direção ao segundo centro de curvatura;
- para uma lente divergente, o raio atravessa a lente numa direção onde seu prolongamento passa pelo primeiro centro de curvatura.
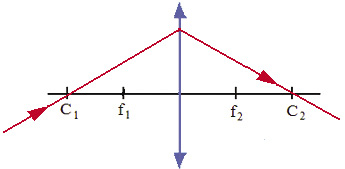
Formação de imagens
Para determinarmos a formação de uma imagem a partir de um objeto posto diante de uma lente, iremos utilizar sempre dois raios notáveis partindo do objeto que incide sobre a lente, e o ponto onde ocorre o cruzamento desses raios será onde irá se formar a imagem.
Lentes convergentes
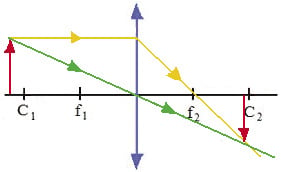
Se o objeto está antes do primeiro centro de curvatura:
- imagem se forma entre os segundos foco e centro de curvatura;
- a imagem é Real, Invertida e Menor.
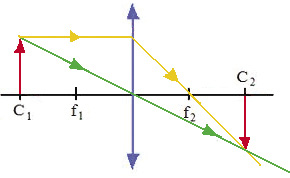
Se o objeto está sobre o primeiro centro de curvatura:
- imagem se forma sob o segundo centro de curvatura;
- a imagem é Real, Invertida e Igual
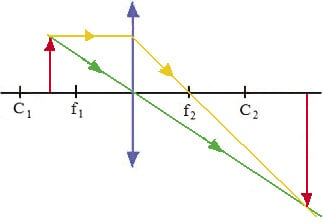
Se o objeto está antes entre os primeiros centro de curvatura e foco:
- imagem se forma depois do segundo centro de curvatura;
- a imagem é Real, Invertida e Maior.
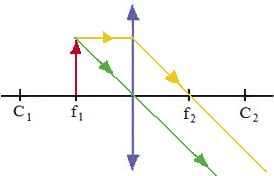
Se o objeto está sobre o primeiro foco:
- imagem não se forma, e é classificada como Imprópria.
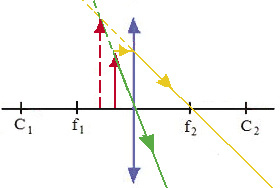
Se o objeto está entre o primeiro foco e o vértice:
- imagem se forma entre o primeiro foco e o vértice, atrás do objeto;
- a imagem é Virtual, Direita e Maior.
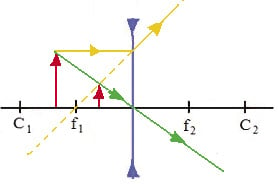
Lentes divergentes
As lentes divergentes possuem apenas um caso. Quando colocamos o objeto em qualquer ponto em relação a lente, a imagem será formada entre o objeto e a lente, e será Virtual, Direita e Menor.
Equação de Gauss
Vamos chamar a posição do objeto como sendo p, a posição da imagem p’. A equação de Gauss relaciona a posição da imagem e do objeto com a posição focal f da lente, e é escrita na seguinte forma:
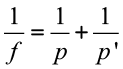
Aumento da imagem
A imagem gerada por uma lente pode ser ampliada ou reduzida. Considerando i como sendo o tamanho da imagem, o o tamanho do objeto, podemos calcular o aumento A como sendo:
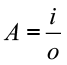
Ainda podemos relacionar o aumento com as posições da imagem e do objeto pela seguinte equação:
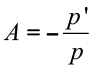
Definição dos sinais
Cada grandeza apresentada, pode ser definida como tendo um valor positivo ou negativo, dependendo de cada condição, que é mostrado na tabela abaixo.
|
A (aumento) |
Imagem direita: positivo |
Imagem invertida: negativo |
|
p (posição do objeto) |
Objeto real: positivo |
Objeto virtual: negativo |
|
p’ (posição da imagem) |
Imagem real: positivo |
Imagem virtual: negativo |
|
f (foco) |
Lente convergente: positivo |
Lente divergente: negativo |
|
i(tamanho da imagem) |
Imagem direita: positivo |
Imagem invertida: negativo |
Saiba mais sobre Lentes Esféricas nesta aula do canal PENSI, disponível no Youtube. Após assistir, revise o que você aprendeu respondendo aos nossos desafios!
[youtube http://www.youtube.com/watch?v=eH8kG6XmPhQ]
Desafios
Questão 01
(CESGRANRIO) Uma lente biconvexa é imersa dois líquidos A e B, comportando-se, ora como lente convergente, ora como lente divergente, conforme indicam as figuras a seguir.
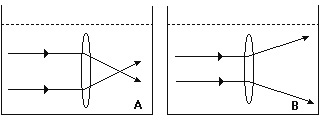
Sendo nA, nB e nC, os índices de refração do líquido A, do líquido B e da lente, respectivamente, então é correto afirmar que:
a) nA < nB < nC
b) nA < nC < nB
c) nB < nA < nC
d) nB < nC < nA
e) nC < nB < nA
Dica 1 – Revise sobre o Princípio de Arquimedes em mais esta aula preparatória para a prova de Física Enem. Estude com a gente para o Exame Nacional do Ensino Médio! – https://blogdoenem.com.br/principio-de-arquimedes-fisica-enem/
Questão 02
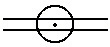
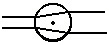
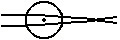
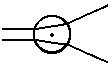
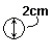
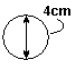
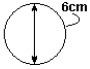
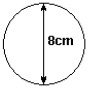
(UERJ) No interior de um tanque de água, uma bolha de ar (B) é iluminada por uma lanterna também imersa na água, conforme mostra a figura seguir. A trajetória de dois raios luminosos paralelos que incidem na bolha, está melhor ilustrada em:
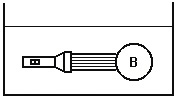
|
a) |
|
|
b) |
|
|
c) |
|
|
d) |
|
Dica 2 – Estude sobre Hidrostática em mais esta aula preparatória para a prova de Física Enem. Revise com a gente para o Exame Nacional do Ensino Médio! – https://blogdoenem.com.br/hidrostatica-fisica-enem/
Questão 03
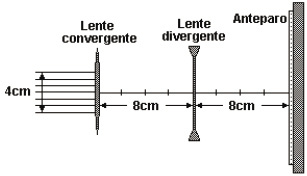
(FUVEST) Um sistema de duas lentes, sendo uma convergente e outra divergente, ambas com distâncias focais iguais a 8 cm, é montado para projetar círculos luminosos sobre um anteparo. O diâmetro desses círculos pode ser alterado, variando-se a posição das lentes. Em uma dessas montagens, um feixe de luz, inicialmente de raios paralelos e 4 cm de diâmetro, incide sobre a lente convergente, separada da divergente por 8 cm, atingindo finalmente o anteparo, 8 cm adiante da divergente. Nessa montagem específica, o círculo luminoso formado no anteparo é melhor representado por
|
a) |
|
|
b) |
|
|
c) |
|
|
d) |
|
|
e) |
|
Dica 3 – Relembre tudo sobre a Lei da Gravitação Universal em mais esta aula de revisão para a prova de Física Enem. O Exame Nacional do Ensino Médio está chegando! – https://blogdoenem.com.br/gravitacao-universal-parte-2-fisica-enem/
Questão 04
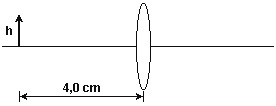
(UFPE) Um objeto de altura h = 2,5 cm está localizado a 4,0 cm de uma lente delgada de distância focal f = +8,0 cm. Determine a altura deste objeto, em cm, quando observado através da lente.
a) 2,5
b) 3,0
c) 4,5
d) 5,0
e) 6,5
Questão 05
(UFJF 2005) Um botânico quer observar detalhes em uma pequena flor. Para isso, ele necessita ampliar cinco vezes a imagem desta flor. Considerando que ele usa uma lupa, cuja lente é delgada e convergente, de distância focal igual a 10 cm, a que distância da lupa deve ficar a flor para se conseguir a ampliação desejada?
a) 2,0 cm
b) 4,0 cm
c) 6,0 cm
d) 8,0 cm
e) 12 cm
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!