Você está se preparando para arrasar no próximo Enem ou vestibular? Então se liga nessa super aula de matemática sobre os Números Naturais! Confira abaixo uma aula completa e uma bateria de exercícios para você fixar bem o conteúdo.
A primeira linguagem numérica que uma criança adquire é a dos Números Naturais. Veja como isso é importante para toda a Matemática.
Ainda muito pequenas as crianças aprendem a contar. Por exemplo, uma criança aprende o número de chocolates que ganha de presente, e logo sabe a diferença entre ter um, dois ou cinco brinquedos. Na linguagem matemática, simbolizamos esse conjunto numérico pela letra ℕ e definimos:
N = {0, 1, 2, 3, 4, 5, 6, 7, …}
Obs: N* = {1, 2, 3, 4, 5, 6, 7, …}. Esse padrão de representação se manterá para os demais conjuntos, isto é, sempre que houver um asterisco sobrescrito, o zero não fará parte do conjunto.
Números Inteiros
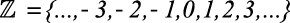
Obs:
1) 
2) 
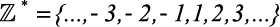
3) 
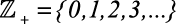(conjunto dos Inteiros não negativos)
4) 
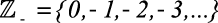(conjunto dos Inteiros não positivos)
5) 
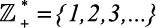(conjunto dos Inteiros positivos)
Números Racionais
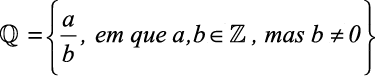
Ou seja, é o conjunto de todos os números que podem ser escritos em forma de fração, com numerador e denominador inteiros, mas com denominador não nulo.
Exemplos:
1) 
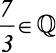
2) 
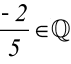
3) 
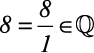(aqui já fica claro que 
).
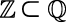E os números representados na forma decimal?
Representação decimal finita
Número com representação decimal finita é Racional.
Exemplos:
1)
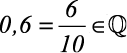
2) 
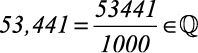
Representação decimal infinita
- Dízima Periódica é Racional
- Dízima Não Periódica não é Racional
Dízima Periódica
Exemplos:
1) 
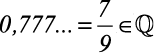. A parte periódica é 7
2) 
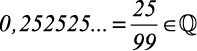. A parte periódica é 25.
Para transformarmos dízimas periódicas em frações, vemos primeiro a quantidade de algarismos do período. No exemplo 1 o período era 7. Como tem apenas um algarismo, dividimos por 9, ou seja, 0,777… = 7/9.
No segundo exemplo o período era 25, número com dois algarismos. Neste caso dividimos por 99, isto é, 0,252525… = 25/99.
A justificativa para o uso de 9 ou 99 ou 999 e assim por diante será dada mais tarde, quando tratarmos do tema Progressão Geométrica.
Dízima Não Periódica
A mais famosa delas é o número
.
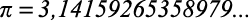Além do Pi, também são dízimas não periódicas os números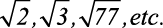 
Como esses números não são Racionais, foi criado um novo conjunto, chamado de:
Números Irracionais
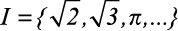
De forma mais palpável, é o conjunto de todos os números cuja representação decimal é infinita e não periódica.
Números Reais
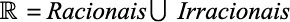
Esquematicamente, temos:
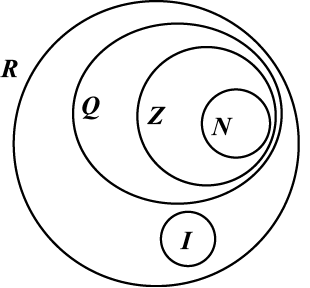
Quer saber mais? Então veja esta videoaula com o professor Lucas, e depois arrase nos exercícios:
Exercícios
Questão 1
(Puccamp 2000) Considere os conjuntos:
IN, dos números naturais,
Q, dos números racionais,
Q+, dos números racionais não negativos,
lR, dos números reais.
O número que expressa
a) a quantidade de habitantes de uma cidade é um elemento de Q+, mas não de IN.
b) a medida da altura de uma pessoa é um elemento de IN.
c) a velocidade média de um veículo é um elemento de Q, mas não de Q+.
d) o valor pago, em reais, por um sorvete é um elemento de Q+.
e) a medida do lado de um triângulo é um elemento de Q.
Questão 2
(FGV) Classifique em verdadeira (V) ou falsa (F) cada uma das sentenças a seguir:
( ) Todo número inteiro positivo é racional.
( ) O número zero é inteiro, natural e racional.
( ) Todo número racional é inteiro.
( ) Todo número racional exato é racional.
( ) Toda dízima periódica é número racional.
Questão 3
(Enem 2ª aplicação 2010) Para dificultar o trabalho de falsificadores, foi lançada uma nova família de cédulas do real. Com tamanho variável – quanto maior o valor, maior a nota – o dinheiro novo terá vários elementos de segurança. A estreia será entre abril e maio, quando começam a circular as notas de R$ 50,00 e R$ 100,00. As cédulas atuais têm 14 cm de comprimento e 6,5 cm de largura. A maior cédula será a de R$ 100,00, com 1,6 cm a mais no comprimento e 0,5 cm maior na largura.
Quais serão as dimensões da nova nota de R$ 100,00?
a) 15,6 cm de comprimento e 6 cm de largura.
b) 15,6 cm de comprimento e 6,5 cm de largura.
c) 15,6 cm de comprimento e 7 cm de largura.
d) 15,9 cm de comprimento e 6,5 cm de largura.
e) 15,9 cm de comprimento e 7 cm de largura.
Questão 4
(Uepg 2010 – adaptado) Assinale V para Verdadeiro ou F para Falso.
( ) O número real representado por 0,5222… é um número racional.
( ) O quadrado de qualquer número irracional é um número racional.
( ) Se m e n são números irracionais então m.n pode ser racional.
( ) O número real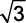 
pode ser escrito sob a forma 
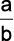, onde a e b são inteiros e b
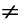0.
( ) Toda raiz de uma equação algébrica do 2º grau é um número real.
Questão 5
(Puc-rio 2007) Os números m e n são tais que 4 ≤ m ≤ 8 e 24 ≤ n ≤ 32. O maior valor possível de m/n é:
a) 1/2
b) 1/3
c) 1/6
d) 1/5
e) 1/8
Texto Complementar: Maior memorização de dígitos do PI. Você sabia dessa? Matheus Norberto de Moraes memorizou 16.110 dígitos em duas horas e 54 minutos, sem nenhuma margem de erro.
O recorde foi conquistado na capital paranaense e acompanhado pelos auditores do Livro dos Recordes Brasileiros. Em duas horas e 54 minutos, Matheus Norberto de Moraes memorizou 16.110 dígitos PI sem nenhuma margem de erro. A cada mil dígitos falados, o recordista fazia uma pausa de 50 segundos para um descanso.
O recordista praticou a memorização de dígitos PI durante três meses e contou com a ajuda de amigos no treinamento. Segundo ele, muitos mnemonistas utilizam a técnica de associação de imagens, figuras, cores, etc., aos números, o que auxilia na memorização. “Cada número que você memorizar é associado a uma imagem, o que possibilita a criação de uma ‘história com os números’. Tudo o que mexe com a nossa emoção, nosso cérebro guarda com mais facilidade”.
Matheus conta também que tem grande facilidade para decorar números e que entrar para o RankBrasil foi um desafio e uma grande conquista em sua vida.
O que é o número PI?
O número PI é a constante matemática que representa a relação entre extensão da circunferência de um círculo e seu diâmetro. Por isto, sempre que dividimos a extensão de qualquer circunferência entre seu diâmetro, obtemos como resultado o número PI.
O PI é um número irracional, que não pode ser escrito como um número finito ou repetindo decimais. O valor aproximado é 3,1416, lembrando que este não é seu valor exato, pois ele continua.
O PI é um dos poucos objetos matemáticos reconhecidos pelo grande público e, apesar de ser conhecido há milhares de anos, ainda é fonte de pesquisas em diversas áreas. Suas propriedades continuam a ser investigadas e novos métodos para calcular seu valor seguem sendo apresentados.
O PI aparece em todas as fórmulas de linhas ou corpos curvos e nos casos mais inesperados, podendo ser usado em áreas que vão da Estatística à Mecânica Quântica.
São conhecidas quatro constantes que podem ser chamadas de PI:
- PI de circunferências: a constante de proporcionalidade na relação entre a circunferência de um círculo e seu diâmetro;
- PI de áreas de círculos: a constante de proporcionalidade na relação entre a área de um círculo e o quadrado de seu diâmetro;
- PI de áreas de esferas: a constante de proporcionalidade na relação entre a área de uma esfera e o quadrado de seu diâmetro;
- PI de volumes de esferas: a constante de proporcionalidade na relação entre o volume de uma esfera e o cubo de seu diâmetro;
Por que é difícil calcular o PI?
A maior dificuldade em calcular o número PI é por se tratar de um número irracional, isto é, que não pode ser expresso como fração entre números inteiros.
Se pudéssemos escrever o PI como fração, na forma m/n, bastaria que definíssemos quais são os números inteiros m e n e, a partir disto, determinar a periodicidade de sua representação decimal.
Existem números irracionais de representação decimal previsível, e então fáceis de calcular, mas PI é um irracional imprevisível e sua representação decimal não mostra nenhuma previsibilidade. Acredita-se que seus algarismos se distribuam aleatoriamente.
Fonte: http://www.rankbrasil.com.br/
