Aprenda aqui tudo o que você precisa para acertar as questões de cálculo de área e de perímetro nas provas de matemática do Enem e do Vestibular. Com as videoaulas da Khan Academy e exercícios online e gratuitos você tira todas as suas dúvidas. Veja abaixo.
Tema recorrente em vestibulares e no Enem, muitas pessoas confundem perímetro com área e se perdem nas contas. Veja aqui como fazer o que é o certo no Cálculo de Área e de Perímetro.
Aprenda aqui com o Blog do Enem e a Khan Academy a diferenciar Perímetro de Área. Veja como fazer Cálculo de Área e de Perímetro facilmente através das principais fórmulas. E, você pode ter certeza, cai sempre nas provas. Todo ano tem questões como estas.
1) Perímetros de figuras planas
Quando falamos de perímetros em matemática, queremos saber o comprimento total da borda da figura, ou seja, o caminho total necessário para percorrer todo o limite da figura geométrica.
Já quando falamos em área, procuramos medir o espaço que a figura preenche.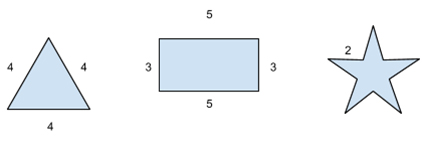
Veja por exemplo as figuras acima: No triângulo, o caminho total ao percorrermos suas bordas é de 4+4+4 = 12 unidades. No caso do retângulo temos 3+5+3+5=16 unidades e na estrela, considerando todos os lados iguais a 2, o perímetro seria 10×2=20 unidades.
2 – Aula Gratuita de Geometria Plana: Área e Perímetro
Veja um resumo simples e rápido com o professor Sérgio Sarkis, do canal Curso Enem Gratuito, para você aprender a fazer os cálculos de Área e de Perímetro nas figuras planas.
Muito boa esta aula. Você aprende mesmo.
3 – Cálculo de Área em figuras planas
Quando queremos pensar no espaço ocupado por uma figura, pensamos na área desta figura. Temos, então, que fazer o cálculo de área. É o que está do ‘lado de dentro’.
Para isso, criamos um pequeno quadrado na unidade de medida desejada e verificamos quantas vezes este quadrado cabe na figura.
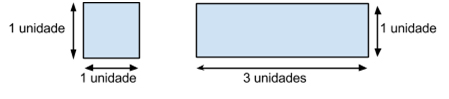
Vemos, por exemplo, que o quadrado à esquerda possui 1 unidade quadrada e cabe no retângulo à direita 3 vezes, ou seja, o triângulo possui 3 unidades quadradas de área.
Vídeo-aula de matemática: Introdução a áreas e unidades quadradas:
Dica do Blog – Você tem dificuldade em Matemática? Veja aqui como participar de um programa especial de aprendizado em matemática da Khan Academy. É gratuito: https://blogdoenem.com.br/matematica-aprenda-khan-academy
4) Perímetro de uma Circunferência
A circunferência possui infinitos lados, assim, o cálculo do perímetro possui uma fórmula especial que envolve o símbolo 
= 3,14
Perímetro da Circunferência: 2 x x r
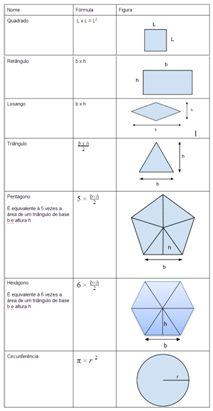
5 – As principais fórmulas da Geometria Plana. Clique na imagem para ampliar:
6 – Desafios para você responder e compartilhar.
1 – (ENEM 2013) Para o reflorestamento de uma área, deve-se cercar totalmente, com tela, os lados de um terreno, exceto o lado margeado pelo rio, conforme a figura. Cada rolo de tela que será comprado para confecção da cerca contém 48 metros de comprimento.
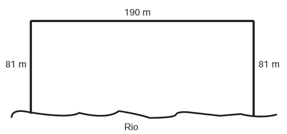
A quantidade mínima de rolos que deve ser comprada para cercar esse terreno é
A) 6.
B) 7.
C) 8.
D) 11.
E) 12.
2 – (ENEM 2013) Uma fábrica de fórmicas produz placas quadradas de lados de medida igual a y centímetros. Essas placas são vendidas em caixas com N unidades e, na caixa, é especificada a área máxima S que pode ser coberta pelas N placas.
Devido a uma demanda do mercado por placas maiores, a fábrica triplicou a medida dos lados de suas placas e conseguiu reuni-las em uma nova caixa, de tal forma que a área coberta S não fosse alterada.
A quantidade X, de placas do novo modelo, em cada nova caixa será igual a:
A) N/9
B) N/6
C) N/3
D) 3/N
E) 9/N
Dica 2 – Gostou do post? Então, agora revise aqui o conteúdo sobre porcentagem, que também cai sempre no Enem e no vestibular: https://blogdoenem.com.br/calculo-porcentagem-matematica-enem/
Pratique com mais exercícios da Khan Academy
Gabarito
1) C ; 2) A
Este post foi escrito pelo professor Alexsandro Sunaga https://www.facebook.com/alexsandro.sunaga. A publicação para você é resultado da parceria da Fundação Lemann com o Blog do Enem – www.fundacaolemann.org.br
