Veja como funciona o GPS e o Google Maps. Estas tecnologias têm como a base gráfica um Plano Cartesiano para apresentar os mapas e os trajetos. Veja abaixo nesta revisão de Matemática para o Enem e Vestibular os fundamentos do Produto Cartesiano.
Para você estudar ‘Funções’, um dos principais conceitos da matemática, é preciso antes revisar Produto Cartesiano. Ajuda você nas provas do Enem, nas provas dos Vestibulares e nas mais variadas disciplinas.
A ideia de Produto Cartesiano é utilizada em varias situações no dia a dia e na educação. Quando você constrói gráficos de funções no ensino fundamental, por exemplo, ou quando localiza uma cidade num mapa utilizado nas aulas de geografia, você está utilizando um Produto Cartesiano.
Quando você olha a tela de um GPS, ou de um itinerário sugerido no Google Maps ligando um ponto a outro, nada mais são do que representações gráficas de um Produto Cartesiano. Percebeu como é útil? Ler e interpretar gráficos e tabelas cai sempre no Enem, e pouca gente acerta. Aprenda, e faça a diferença.
PRODUTO CARTESIANO
Considerando os conjuntos A = {1 , 2 , 3} e B = { 1, 5 } vamos construir um novo conjunto indicado por A x B cujos elementos são pares ordenados formados pelos elementos de A e de B, ou seja, o primeiro elemento pertence ao conjunto A e o segundo elemento pertence ao conjunto B. Assim, chamaremos de produto cartesiano de A por B o conjunto:
A x B = {(1,1) , (1,5), (2,1), (2,5), (3,1), (3,5)}
A noção de par ordenado é importante, pois ela representa a ordem em que os elementos aparecem no par de números.
Note que no conjunto A x B acima o par ordenado (2,1) é diferente do par ordenado (1,2), sendo que este último não pertence ao conjunto em questão, pois o elemento 2 não pertence ao conjunto B.
Dica 1 – O que mais cai em Matemática nos Vestibulares e no Enem? Veja aqui as melhores dicas https://blogdoenem.com.br/category/cainaprova/matematica/
Saiba mais sobre produto cartesiano assistindo a esta vídeo aula totalmente gratuita do professor Lucas, do canal Curso Enem Gratuito e mande bem nas questões de matemática dos vestibulares e também do Enem.
Pares Ordenados
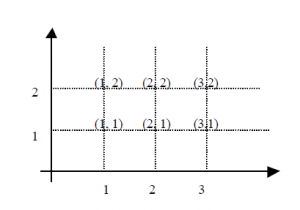
Tomemos dois eixos perpendiculares sobre os quais representamos o conjunto A (primeiro conjunto) no eixo horizontal e o conjunto B (segundo conjunto) no eixo vertical. Os pares ordenados podem ser representados pelas retas paralelas aos eixos que passam pelos pontos que representam os elementos de A e de B. Veja o exemplo abaixo:
Exemplo: Sejam os conjuntos A = {1 ,2 , 3} e a representação gráfica do produto cartesiano A x B será:
Dica 2 – Apostila Gratuita de Matemática – Revisão com exercícios sobre o que mais cai nas provas do Enem e nos Vestibulares: https://blogdoenem.com.br/apostila-enem-gratuita-matematica/
Exercício – (Enem 2011) – O termo agronegócio não se refere apenas à agricultura e à pecuária, pois as atividades ligadas a essa produção incluem fornecedores de equipamentos, serviços para a zona rural, industrialização e comercialização dos produtos. O gráfico seguinte mostra a participação percentual do agronegócio no PIB brasileiro:
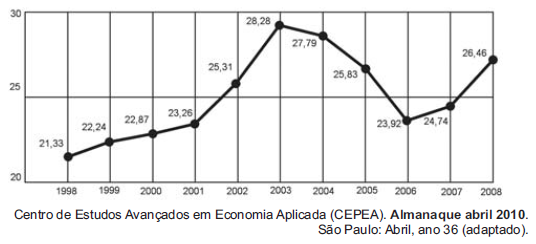
Esse gráfico foi usado em uma palestra onde o orador ressaltou uma queda da participação do agronegócio no PIB brasileiro e a posterior recuperação dessa participação, em termos percentuais.
Segundo o gráfico, o período de queda ocorreu entre os anos de:
a) 1998 e 2001
b) 2001 e 2003
c) 2003 e 2006
d) 2003 e 2007
e) 2003 e 2008
Resposta: Observando o gráfico fica evidente que a queda se dá de 2003 para 2004 onde os valores percentuais passam de 28,28 para 27,79 respectivamente, no ano de 2004 para 2005, onde os valores passam de 27,79 para 25,83 e de 2005 para 2006 onde os valores passam de 25,83 para 23,92. Logo há queda desde o ano de 2003 até o ano de 2006. Desta forma a resposta correta é a alternativa c.
Dica 3 – Razão e Proporção – Cai sempre nas provas de Matemática, e também para resolver questões de Química, Física e Biologia. Revisão grátis de Razão e Proporção com aulas da Khan Academy: https://blogdoenem.com.br/enem-khan-academy-2/.




