Revise os fundamentos da trigonometria com a demonstração do Teorema de Pitágoras e o básico das relações métricas do Triângulo Retângulo para fazer o nosso simulado!
O básico do Teorema de Pitágoras e do Triângulo Retângulo você já sabe: a soma do quadrado dos catetos é igual ao quadrado da hipotenusa. Mas, o fundamental é ‘entender’ o que isto significa.
Observe com calma a imagem e tente abstrair este teorema a partir da ilustração:
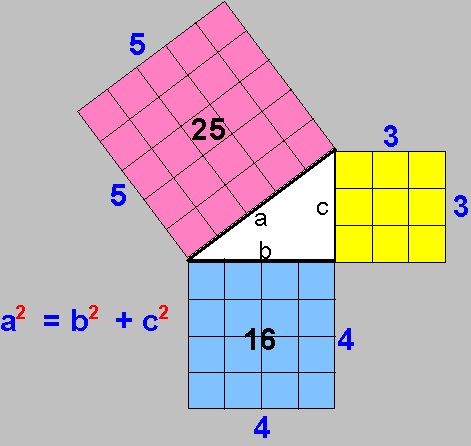
Perceba que:
- Sobre a letra “a“, acima da hipotenusa, estão 25 quadradinhos.
- Abaixo do cateto da letra”b“, estão 16 quadradinhos.
- E, ao lado do cateto da letra “c“, estão 9 quadradinhos.
Agora, some os quadradinhos dos catetos b e c, para ver quanto dá essa conta.
Teorema de Pitágoras
Somou? Então , você tem na soma dos quadrados de b + c a mesma quantidade dos quadradinhos de a. É o Teorema de Pitágoras:
![]()
Mas, o que significa isso para o mundo da Matemática?
Assista à videoaula sobre o Teorema de Pitágoras com o professor de matemática Lucas Borguezan, do canal do Curso Enem Gratuito, antes de continuar a sua revisão:
Triângulo Retângulo
Um triângulo retângulo, em geometria, é um triângulo em que um dos ângulos é reto. A relação entre os lados e os ângulos de um triângulo retângulo é a base da trigonometria. O lado oposto ao ângulo reto é chamado de hipotenusa. Os lados adjacentes ao ângulo reto são chamados de catetos. Observe melhor na imagem:
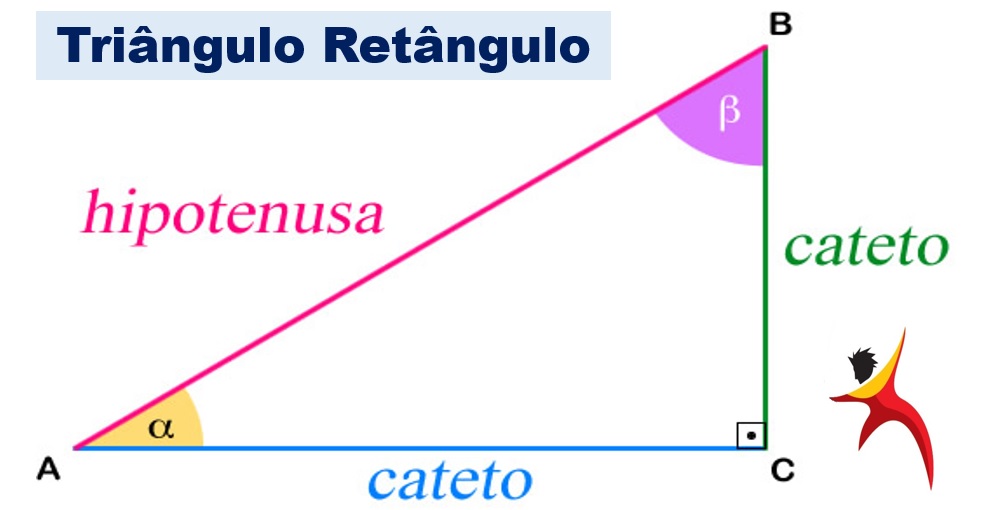
O triângulo retângulo é uma das figuras geométricas mais utilizadas para solucionar cálculos de volume e de área, sendo que o Teorema de Pitágoras é a base para os cálculos trigonométricos.
Os cálculos algébricos envolvendo o Triângulo Retângulo partem de propriedades que nos permitem saber que calcular as medidas dos demais lados e ângulos se você tiver os dados (medidas) de dois lados e mais a medida de um dos ângulos agudos.
Triângulo Retângulo e Teorema de Pitágoras
Antes de continuar, assista à aula gratuita do canal Curso Enem Gratuito, com o professor Sérgio Sarkis, com a revisão completa das relações trigonométricas decorrentes do triângulo retângulo e o Teorema de Pitágoras.
Na solução dos problemas sobre o triângulo retângulo, vamos aplicar um conjunto de fórmulas denominadas relações métricas, que relacionam as medidas dos lados do triângulo e suas projeções entre si.
Para isso vamos representar o triângulo retângulo apoiado sobre a hipotenusa:
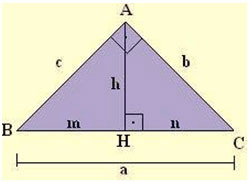 Na representação acima, temos:
Na representação acima, temos:
- Hipotenusa = a
- Catetos = b e c
- Altura relativa à hipotenusa = h
- Projeções dos catetos sobre a hipotenusa = m e n
Relações métricas e o Teorema de Pitágoras
Você já sabe que a fórmula do Teorema de Pitágoras é a soma do quadrado dos catetos é igual ao cateto da hipotenusa. Agora, tente fazer uma representação mental da atuação nos cálculos de um triângulo retângulo.
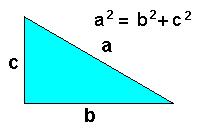
Exercício resolvido sobre relações métricas no triângulo
Veja agora o que são o cateto oposto e o adjacente, e como fazer a resolução de problemas básicos:
Resumo sobre o Teorema de Pitágoras
Confira uma demonstração do Teorema de Pitágoras com a visualização da área gerada pelo quadrado da hipotenusa e pelo quadrado de cada um dos catetos.
Observe na demonstração gráfica do Teorema de Pitágoras na imagem abaixo que se você somar as áreas geradas pelos quadrados dos catetos, vai encontrar exatamente a mesma área gerada pelo quadrado da hipotenusa.
Simulado: o Teorema de Pitágoras
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta

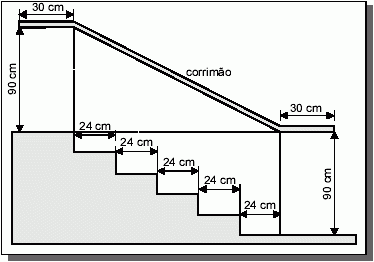
(ENEM) Na figura acima, que representa o projeto de uma escada com 5 degraus de mesma altura, o comprimento total do corrimão é igual a:
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 2 de 10
2. Pergunta
Diariamente, uma residência consome 20 160 Wh. Essa residência possui 100 células solares retangulares (dispositivos capazes de converter a luz solar em energia elétrica) de dimensões 6 cm ×× 8 cm. Cada uma das tais células produz, ao longo do dia, 24 Wh por centímetro de diagonal. O proprietário dessa residência quer produzir, por dia, exatamente a mesma quantidade de energia que sua casa consome.
Qual deve ser a ação desse proprietário para que ele atinja o seu objetivo?
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 3 de 10
3. Pergunta
(UERJ) Millôr Fernandes, em uma bela homenagem à Matemática, escreveu um poema do qual extraímos o fragmento abaixo:
Às folhas tantas de um livro de Matemática,
um Quociente apaixonou-se um dia doidamente
por uma Incógnita.
Olhou-a com seu olhar inumerável
e viu-a do ápice à base: uma figura ímpar;
olhos rombóides, boca trapezóide,
corpo retangular, seios esferóides.
Fez da sua uma vida paralela à dela,
até que se encontraram no Infinito.
“Quem és tu?” – indagou ele em ânsia radical.
“Sou a soma dos quadrados dos catetos.
Mas pode me chamar de hipotenusa.”
………………………………………………………………………..
(Millôr Fernandes. Trinta Anos de Mim Mesmo.)A Incógnita se enganou ao dizer quem era. Para atender ao Teorema de Pitágoras, deveria dar a seguinte
resposta:Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 4 de 10
4. Pergunta
(ENEM) Uma escada medindo 4 metros tem uma de suas extremidades apoiada no topo de um muro, e a outra extremidade dista 2,4 m da base do muro. A altura desse muro é:
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 5 de 10
5. Pergunta
(PUC) A soma dos quadrados dos três lados de um triângulo retângulo é igual a 32. Quanto mede a hipotenusa do triângulo?
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 6 de 10
6. Pergunta
(ENEM) As diagonais do losango medem 8 cm e 6 cm.

O polígono (parcialmente desenhado) tem o perímetro de (em cm):
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 7 de 10
7. Pergunta
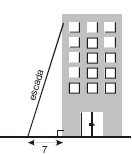
(OBMEP) O topo de uma escada de 25 m de comprimento está encostado na parede vertical de um edifício. O pé da escada está a 7 m de distância da base do edifício, como na figura. Se o topo da escada escorregar 4m para baixo ao longo da parede, qual será o deslocamento do pé da escada?
 Correto
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 8 de 10
8. Pergunta
(ENEM)A diagonal de um retângulo mede 10 cm, e um de seus lados mede 8 cm. A superfície desse retângulo mede:
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 9 de 10
9. Pergunta
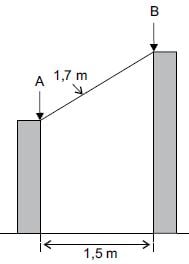
(Vunesp) Duas estacas de madeira, perpendiculares ao solo e de alturas diferentes, estão distantes uma da outra, 1,5 m. Será colocada entre elas uma outra estaca de 1,7 m de comprimento, que ficará apoiada nos pontos A e B, conforme mostra a figura.

A diferença entre a altura da maior estaca e a altura da menor estaca, nessa ordem, em cm, é:
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 10 de 10
10. Pergunta
(SAP-SP) Roberto irá cercar uma parte de seu terreno para fazer um canil. Como ele tem um alambrado de 10 metros, decidiu aproveitar o canto murado de seu terreno (em ângulo reto) e fechar essa área triangular esticando todo o alambrado, sem sobra. Se ele utilizou 6 metros de um muro, do outro muro ele irá utilizar, em metros,
Correto
Parabéns! Siga para a próxima questão.