Triângulos: Definição e Propriedades: veja no resumo Enem

Como você já sabe, o triângulo é uma figura plana formada por três segmentos de retas. Serão estudados nesta aula os elementos geométricos que compõem essa figura bem como as propriedades pertinentes a esses elementos.

Definição e Propriedades dos Triângulos

Triângulo é uma figura plana, formada por três segmentos de reta delimitando uma região fechada. Na figura identificam-se os seguintes elementos: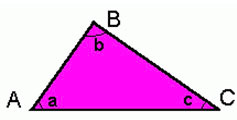

1. ) Vértices: são os pontos A, B e C
2. ) Ângulos internos: a, b e c
3. ) Lados: AB, AC e BC

 

Altura: é um segmento de reta traçado a partir de um vértice de forma a encontrar o lado oposto ao vértice formando um ângulo reto (90º). BH é uma altura do triângulo.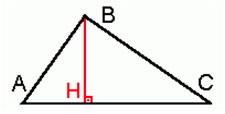

Ângulo externo: é formado por um dos lados do triângulo e pelo prolongamento do lado adjacente.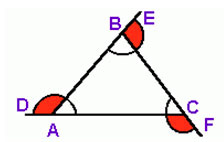Na figura são ângulos externos os ângulos D, E, F.

1. ) A soma dos ângulos internos de qualquer triângulo é sempre igual a 180º.
2. ) A soma dos ângulos externos de qualquer triângulo é sempre igual a 360º.
3. ) Cada ângulo externo é igual à soma dos outros dois internos não adjacentes a ele.
4. ) O maior lado do triângulo está sempre oposto ao maior ângulo desse triângulo.

 

Dicas sobre as Propriedades dos Triângulos

Perímetro = observe na imagem que o perímetro nada mais é que soma dos lados  do triângulo = AB + AC + BC 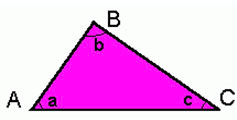Viu como é simples fazer o cálculo do perímetro?

 

Classificação & Definição dos Triângulos

1 – O triângulo equilátero possui todos os lados congruentes.

Pode-se verificar que um triângulo equilátero é também equiângulo, ou seja, possui todos os seus ângulos internos congruentes (e com medida 60°). Por este motivo, este tipo de triângulo é também um polígono regular.

2 – O triângulo isósceles possui pelo menos dois lados congruentes. Neste triângulo o ângulo formado pelos lados congruentes denomina-se ângulo do vértice.

Os demais ângulos do Triângulo Isósceles denominam-se ângulos da base e, como se pode verificar, são congruentes. Note que os triângulos equiláteros também são isósceles.

3 – Em um triângulo escaleno as medidas dos três lados são diferentes. É possível mostrar que os ângulos internos de um triângulo escaleno também possuem medidas diferentes.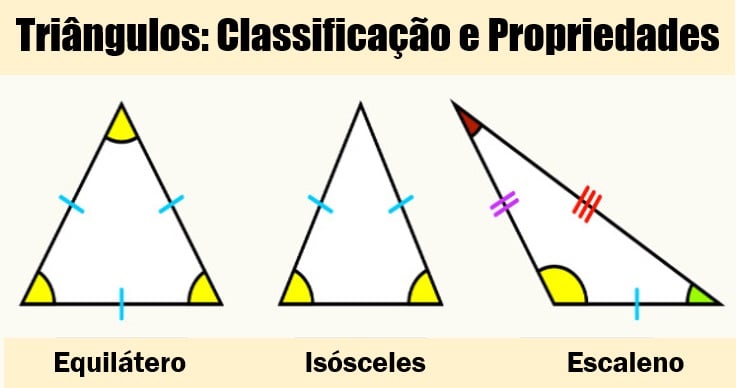Veja na imagem acima os triângulos Equilátero, Isósceles, e Escaleno.

Resumo sobre Definição e Propriedades

Confira com o professor Sérgio Sarkis uma aula-show com o básico sobre a Definição e as Propriedades dos Triângulos.

Gostou do resumo? Têm mais aulas de matemática com ele sobre a classificação dos triângulos no canal do Curso Enem Gratuito.

Entenda a Base do Triângulo:

1) Denomina-se base o lado sobre qual apoia-se o triângulo.

2) No triângulo isósceles, considera-se base o lado de medida diferente e sobre ele estarão localizados os ângulos congruentes (iguais) do triângulo.

O Triângulo Equilátero – Este triângulo abaixo é equilátero, pois possui os três lados congruentes.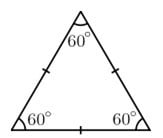Em particular, como seus lados são dois a dois congruentes, ele é um triângulo isósceles. Pode-se observar que todos os seus ângulos internos medem 60° e por isso ele é equiângulo.

O Triângulo isósceles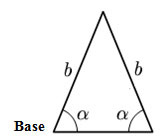

Neste triângulo há somente dois lados congruentes: os que têm medida b. Por este motivo, o triângulo é isósceles, mas não é equilátero.  Além disso, cada um destes dois lados forma um ângulo de medida α com a base do triângulo.

O Triângulo escaleno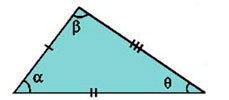Aqui, cada um dos lados tem um comprimento diferente dos demais. Observe ainda que todos os seus ângulos internos são diferentes entre si.

Classificação dos ângulos internos

Um triângulo também pode ser classificado de acordo com seus ângulos internos:

Um triângulo retângulo possui um ângulo reto. Num triângulo retângulo, denomina-se hipotenusa o lado oposto ao ângulo reto. Os demais lados denominam-se catetos. Veja: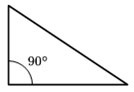Observe o ângulo reto (90º)

 

Um triângulo obtusângulo possui um ângulo obtuso e dois ângulos agudos: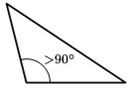Veja na figura que há um ângulo obtuso (> 90º), e dois ângulos agudos.

 

Em um triângulo acutângulo, todos os três ângulos são agudos. Veja na imagem que todos os ângulos são menores que 90º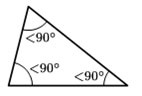Todos os três ângulos são agudos (< 90º).

Responde rápido para testar seu nível:

1) Existe triângulo retângulo isósceles?

Sim ( ) Não ( )

2) Existe triângulo retângulo equilátero?

Sim ( ) Não ( )

3) Existe triângulo retângulo escaleno?

Sim ( ) Não ( )

4) Todo triângulo equilátero é isósceles?

Sim ( ) Não ( )

O Teorema de Pitágoras

Saiba mais sobre Classificação e Propriedades dos Triângulos Retângulos nesta aula sobre o Teorema de Pitágoras.  Após assistir, revise o que você aprendeu respondendo aos nossos desafios!

Muito bom este resumo do professor Sérgio Sarkis! Tudo a ver com a Definição e as Propriedades dos Triângulos

Exercícios sobre Triângulos

Questão 1 – Determinar o valor de x + y na figura abaixo sabendo que os ângulos A e B são congruentes:

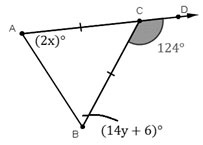
a) 30

b) 31

c) 34

d) 35

e) 40

Questão 2

Bissetriz é a linha que divide um ângulo em duas partes iguais. O triângulo MNP é tal que ângulo M = 80° e ângulo P = 60°. A medida do ângulo agudo formado pela bissetriz do ângulo interno N com a bissetriz do ângulo externo P é:

• a) 20°
• b) 30°
• c) 40°
• d) 50°
• e) 60°

 

Questão 3 – Um triângulo isósceles tem um dos ângulos internos iguais a 100°. Qual é o valor do menor ângulo deste triângulo?

• a) 20º
• b) 30º
• c) 40º
• d) 45º
• e) 50º

 

Questão 4

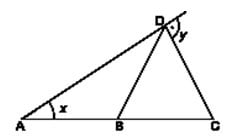
• Questão 5 – Na figura abaixo temos que AB = BD = CD. Então:a) y = 3x
• b) y = 2x
• c) y = x
• d) x + y = 180°
• e) 3x = 2y

 

Questão 6 – Considere um triângulo equilátero de lado ℓ como mostra a figura a seguir. Unindo-se os pontos médios dos seus lados obtemos 4 (quatro) novos triângulos. O perímetro de qualquer um destes quatro triângulos é igual a: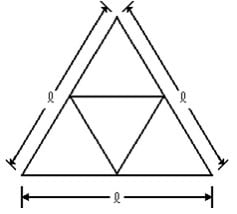

 

Questão 7 – Na figura a seguir AB = AC, BX = BY e CZ = CY. Se o ângulo A mede 40°, então o ângulo XYZ mede: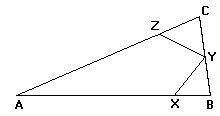

• a) 40°
• b) 50°
• c) 60°
• d) 70°
• e) 90°