Algumas matrizes, dependendo de sua ordem, tornam-se difíceis para calcular o seu determinante. Nesta aula serão apresentados dois métodos que vão facilitar esse cálculo: Teorema de Laplace e Regra de Chió. Venha fazer parte desta aula e arrase em matemática no Enem!
Nos cálculos dos determinantes, as regras práticas se estendem, em sua maioria, apenas para as matrizes quadradas de ordem igual ou menor que três. Para calcular o determinante das demais, é necessário usar o teorema de Laplace.
O teorema de Laplace consiste em escolher uma das filas (linha ou coluna) da matriz e somar os produtos dos elementos dessa fila pelos seus respectivos cofatores.
Para tanto, veremos primeiramente o cálculo dos cofatores e assim, aplicaremos o Teorema de Laplace.
Dica 1: Determinante? Você não lembra desse conteúdo? Então, veja este excelente post da professora Jaceli: https://blogdoenem.com.br/determinantes-definicao-calculo/




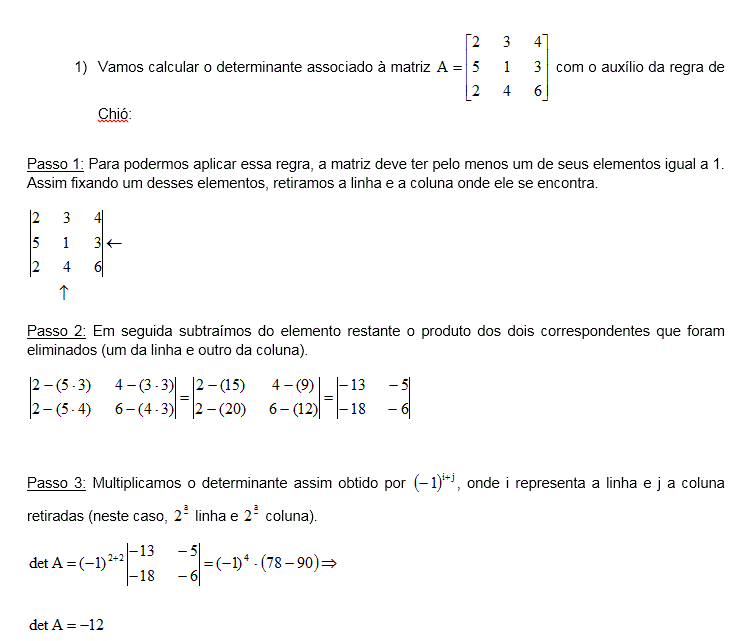
Para finalizar sua revisão, confira a aula abaixo e se garanta no Teorema de Laplace!