Aprenda os macetes com o Círculo Trigonométrico para gabaritar nas questões mais difíceis de matemática. Revise as características das circunferências, conheça e aprenda a classificar os elementos. Veja o que é Tangente, Secante, e Cotangente. Agora, no resumo Enem.
As circunferências possuem características não comumente encontradas em outras figuras planas, como o fato de ser a única figura plana que pode ser rodada em torno de um ponto sem modificar sua posição aparente. É também a única figura que é simétrica em relação a um número infinito de eixos de simetria.
A circunferência é importante em praticamente todas as áreas do conhecimento como nas Engenharias, Matemática, Física, Química, Biologia, Arquitetura, Astronomia, Artes e também é muito utilizada na indústria e no seu cotidiano.
Confira tudo sobre circunferêncisa com esta aula e arrase em matemática no Enem! O primeiro passo é você conhecer as definições básicas de Raio, Arco, Corda, Diâmetro, e como os ângulos fazem parte da essência trigonométrica.
Os ângulos na Circunferências
Confira agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito.
Podemos dizer que todo polígono regular pode ser inscrito ou circunscrito a uma circunferência. Isso quer dizer que em todo polígono regular podemos “desenhar” uma circunferência no seu interior e no seu exterior.
Caso a circunferência esteja no interior do polígono, dizemos que a circunferência está inscrita ao polígono ou que o polígono está circunscrito à circunferência.
Por outro lado, caso a circunferência esteja no exterior do polígono, dizemos que a circunferência está circunscrita ao polígono ou que o polígono está inscrito à circunferência.
Nesta aula acima, o professor Lucas vai te introduzir nos cálculos de ângulos da circunferência. E, no resumo abaixo, confira os exemplos com exercícios resolvidos sobre os ângulos nas CIrcunferências:
Exercícios sobre os ângulos na Circunferência:
Elementos das Circunferências
Circunferência é o conjunto de todos os pontos de um plano equidistantes de um ponto fixo, desse mesmo plano, denominado centro da circunferência. Algumas definições
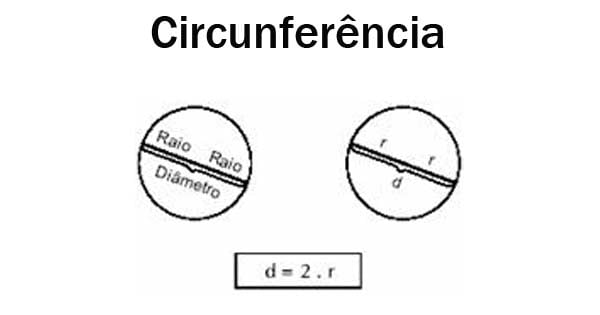
Raio – Raio de uma circunferência (ou de um círculo) é um segmento de reta com uma extremidade no centro da circunferência e a outra extremidade num ponto qualquer da circunferência.
Arco – é uma parte da circunferência limitada por dois pontos, que se chamam extremidades do arco.
Corda – é um segmento de infinitos pontos alinhados, cujos pontos extremos com um ponto da circunferência. Quando esse segmento passa pelo centro da circunferência, temos o que chamamos de diâmetro.
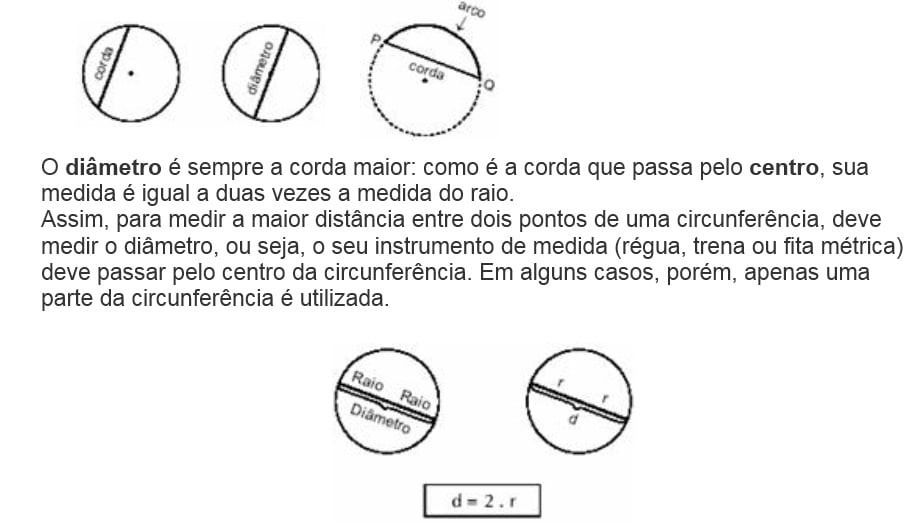
Tangente – é a reta que tem um único ponto comum à circunferência, este ponto é conhecido como ponto de tangência ou ponto de contato.
Secante – é a reta que intercepta a circunferência em dois pontos distintos, se essa reta intercepta a circunferência em dois pontos quaisquer, podemos dizer também que é a reta que contém uma corda.
Para simbolizar a corda que une os pontos P e Q, utilizamos a notação de segmento de reta, ou seja, corda PQ.
Por outro lado, o arco também começa em P e termina em Q mas, como você pode ver, a corda e o arco são diferentes e por isso a simbologia também deve ser diferente. Para o arco, usamos PQ.
Da mesma forma que a maior corda é o diâmetro, o maior arco é aquele que tem as extremidades em um diâmetro. Esse arco é chamado semicircunferência, e a parte do círculo correspondente é chamada semicírculo.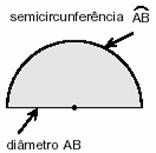
O Círculo Trigonométrico
Veja agora os macetes para resolver questões sobre Cícrulos e Circunferências nas provas do Enem e dos vestibulares. Veja o fantástico Círculo Trigonométrico.
As dicas do professor Lucas:
- O círculo trigonométrico, às vezes chamado também de ciclo trigonométrico é uma ferramenta importante no estudo da trigonometria e facilita muito a resolução de exercícios.
- O ciclo trigonométrico é um círculo de raio 1. Ou seja, do seu cento até a borda, a medida é 1. Assim, podemos definir todos os valores de seno e cosseno que existem, uma vez que o círculo trigonométrico compreende todos os ângulos.
- Na trigonometria, seno e cosseno são chamados de razões trigonométricas. Para medir o valor do seno, é comum usar o eixo vertical do círculo trigonométrico. Desta forma, o eixo vertical do ciclo trigonométrico é chamado eixo dos senos.
- Por outro lado, podemos encontrar o valor do cosseno no eixo horizontal, de maneira que este é chamado de eixo dos cossenos.
- Um exemplo muito legal de usar o círculo trigonométrico é conhecer também a tabela de ângulos notáveis, que traz os valores de seno, cosseno e tangente dos ângulos notáveis: 30º, 45º e 60º.
- Muitas vezes, o ângulo trabalhado em uma questão é diferente, mas, desenhando-o no círculo trigonométrico, verificamos que ele tem simetria com um dos ângulos notáveis.
- Desta maneira, já temos as razões trigonométricas, ou seja, o valor do seno, cosseno ou tangente pedido pelo exercício!
Comprimento de uma circunferência
Quando medimos os lados de uma região, estamos determinando o valor do seu perímetro. No caso das regiões circulares não podemos adotar tal metodologia, pois não podemos definir a medida dos lados desse tipo de região. Para determinar a medida do comprimento de uma região circular, utilizamos a medida de seu raio, mas somente isso não é suficiente.
Devido à relação comprimento/diâmetro nas regiões circulares, conseguimos descobrir um valor constante, aproximadamente igual a 3,14. Esse número irracional ficou conhecido por “pi”, o qual é representado pelo símbolo π. Em qualquer região circular basta dividirmos o comprimento da mesma, pela medida do diâmetro, que encontraremos o valor correspondente a 3,14 aproximadamente.
Com base nessa descoberta, o comprimento de uma região limitada pelas circunferências é calculada através da expressão matemática C = 2.π.r. Por exemplo, se uma região circular possui raio medindo 8 metros, seu comprimento será calculado da seguinte maneira:
Exercícios sobre Círculos e Circunferências
Exercício – 1 (UESPI) Um trabalhador gasta 3 horas para limpar um terreno circular de 6 metros de raio. Se o terreno tivesse 12 metros de raio, quanto tempo o trabalhador gastaria para limpar tal terreno?
a) 6 h.
b) 9 h.
c) 12 h.
d) 18 h.
e) 20 h.
R: C
Exercício – 2 (USP) Se M é o ponto médio do segmento AB e P é o ponto médio do segmento OM, determinar a equação da circunferência de centro P e raio OP.
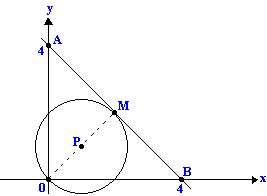
R: (x – 1)2 + (y-1)2 = 2
Exercício – 3 (Furb – SC) “Lixo é basicamente todo e qualquer resíduo sólido proveniente das atividades humanas ou gerado pela natureza em aglomerados urbanos. O lixo faz parte de nossa vida e tratá-lo bem é uma questão de bom senso, cidadania e bem-estar agora e principalmente no futuro.”(www.loucosporlixo.com.br). Pensando nisso, um grupo teatral quer representar uma peça sobre a importância da reciclagem do lixo. Eles querem montar um cenário no qual 3 paredes de 4 m de altura por 5 m de comprimento deverão ser revestidas de CDs defeituosos. Sabendo-se que cada CD possui 12 cm de diâmetro, quantos Cds, aproximadamente, serão necessários para revestir essas paredes? (Use π = 3,14.)
a) 5200
b) 5300
c) 5400
d) 5500
e) 5600
R: B
Curso Enem Gratuito
Quer aumentar suas chances no próximo Exame Nacional do Ensino Médio e mandar bem nas Notas de Corte do Enem? Estude com as apostilas e aulas gratuitas do Curso Enem Online. Todas as matérias do Exame e ainda as Dicas de Redação. Acesse aqui o Curso Enem Gratuito Online.
Acesse aqui os Aulões do Blog do Enem! São videoaulas gratuitas e completas com os conteúdos mais relevantes para o Exame Nacional do Ensino Médio.