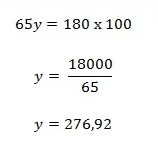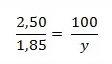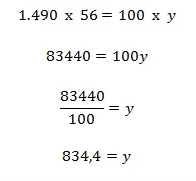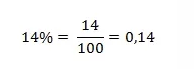Veja como calcular o aumento percentual em um preço. Aprenda a resolver problemas de porcentagem. Cai direto no Enem, no Encceja e nos Vestibulares. É você com a mão no Diploma do Ensino Médio, e com o passaporte para a Universidade. Vem!
Você sabe calcular o aumento percentual no preço de um pé de alface que ontem custava R$ 2,50 e hoje custa R$ 4,35? Não? Pois saiba que a matéria de porcentagem é um conteúdo essencial não só para o seu cotidiano, mas também para arrebentar nas questões de matemática dos vestibulares e, principalmente, do Enem e do Encceja (que adora explorar este tipo de conteúdo)!
Primeiramente, devemos conhecer o que é porcentagem. Porcentagem é uma fração cujo denominador é 100. Ela indica uma taxa ou proporção. Podemos resolver problemas que envolvem o cálculo de porcentagem de três formas:
- Pela forma fracionária,
- Pela regra de três simples; e,
- Pelo fator multiplicação.
Veja neste post diversos exemplos de problemas envolvendo o Cálculo de Porcentagem e as formas de solução utilizando as alternativas 1, 3 e 3 citadas acima. Então, que tal aprender como resolver problemas de porcentagem para arrebentar no Enem?
- Como já mencionamos, porcentagem é uma fração cujo denominador é 100. Veja nos exemplos 5/100; que você pode ler 5% (cinco por cento), e assim sucessivamento no 89/100, e no 25/100. Observe os exemplos:
 Os termos 5%, 89% e 25% são chamados de taxas percentuais.
Os termos 5%, 89% e 25% são chamados de taxas percentuais. - Eles também podem ser apresentados nas formas Decimais: 0,05; 0,89 e 0,25.
- Para transformara taxa percentual na forma decimal, devemos escrever a taxa em forma de fração e depois realizar a divisão entre o numerador e o denominador.
Exemplo: qual a forma decimal que representa a taxa 34%?
- Solução:
- Etapa 1 – Escreveremos 34% na forma de fração, inicialmente, ou seja,

- Etapa 2 – Agora, basta dividir o numerador pelo denominador para encontrar a forma procurada.
- Etapa 3 – Portanto, 34% = 0,34. Pronto! Agora vejamos alguns exemplos de problemas envolvendo porcentagem.
Aula gratuita com o resumo do Cálculo de Porcentagem
Veja com o professor Sérgio Sarkis, do Curso Enem Gratuito, um resumo simples e rápido para você aprender de vez a resolver Cálculo de Porcentagem:
Viu como é simples? Podemos também resolver problemas de porcentagem utilizando a regra de três simples. Então, agora vamos continuar.
Calculando descontos ou acréscimos com a forma fracionária.
Exemplo 1: O consumo mensal de energia elétrica em uma escola é de 145 Kwh. Esse mês, o consumo teve um aumento de 25% devido ao uso do condicionador de ar. Qual foi o consumo de Kwh no mês?
Solução:
Escrevemos 25% em forma de fração.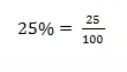
Podemos determinar agora, o quanto a fração acima corresponde de 145, da seguinte forma: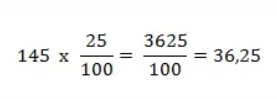 Devemos somar o valor encontrado com o 145 Kwh. Logo, temos que o consumo desse mês foi 145 Kwh + 36,25 Kwh = 181,25 Kwh.
Devemos somar o valor encontrado com o 145 Kwh. Logo, temos que o consumo desse mês foi 145 Kwh + 36,25 Kwh = 181,25 Kwh.
Note que calcular o aumento ou desconto em um determinado produto é como uma receita de bolo, que vamos repassar para você. Anote aí! Dada uma taxa percentual de desconto ou acréscimo sobre uma quantia, para calcular o novo montante deverá:
- Reescrever a taxa percentual em fração com denominador 100;
- Multiplicar a quantia inicial pela fração encontrada;
- Somar (se acréscimo) ou diminuir (se desconto) da quantia inicial, resultando no montante (quantia final) procurado.
Macete para o cálculo de Porcentagem
Veja agora com o professor Lucas Borguesan, do canal do Curso Enem Gratuito, as dicas iniciais para você gabaritar Porcentagem:
Gostou do resumo com o professor Lucas? Então, você pode fazer com ele o Curso Gratuito de Matemática Básica. São dez aulas com dicas e simulados, tudo grátis. As Inscrições estão abertas, e você pode começar agora.
Cálculo de porcentagem com Regra de Três
Exemplo 2: O preço do videogame com 35% de desconto é de R$ 180,00. Qual é o preço do videogame sem o desconto?
Solução:
- Inicialmente, vamos calcular a qual porcentual corresponde os R$ 180,00.
- O preço do videogame, sem o desconto, corresponde a 100%.
- Assim o valor, com o desconto, corresponde à diferença entre os 100% e o percentual de desconto:
-
100% – 35% = 65%
Aplicando a regra de três simples, obtemos:
- y ____________________ 100%
- 180,00 _________________ 65%
- Reescrevendo as equivalências acima, temos a proporção:
 Aplicando a propriedade fundamental da proporção, segue a igualdade:
Aplicando a propriedade fundamental da proporção, segue a igualdade:
- Logo, o preço do videogame, sem desconto, é de R$ 276, 92.
Razão e Proporção
Você percebeu que utilizamos o termo “proporção”? Você lembra o que é uma proporção? Caso não lembre, volte nesta aula sobre escala, razão e proporção para refrescar a memória.
Agora, você lembra o problema da Maria, aquela menina que vai à feira toda semana? O problema da Maria é diferente dos exemplos apresentados acima. Nele buscamos o valor da taxa percentual, o que é diferente do que calculamos até o momento. Vamos ajudar a Maria?
Maria pagava até semana passada R$ 2,50 pelo pé da alface. Nessa semana ela pagou R$ 4,35 reais pela mesma verdura. Queremos saber qual foi o aumento percentual. Vamos às contas então!
Solução:
- Primeiro, calcularemos o valor do aumento no preço do pé de alface.
- 4,35 – 2,50 = 1,85
- Agora, aplicando a regra de três simples temos:
- 2,50 __________________ 100%
- 1,85 ___________________ y
Montando a proporção, obtemos:
Aplicando a propriedade fundamental da proporção o valor de y será: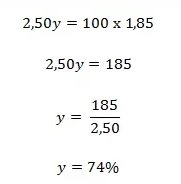
Portanto, a taxa percentual de aumento no preço do pé de alface foi de 74%.
Resolução com a Regra de Três
Utilizando a regra de três, podemos resolver problemas diferentes dos vistos até agora. Veja um exemplo.
Exemplo 3: Em uma escola foram entrevistados 1.490 alunos. Dos alunos entrevistados, 56% possuem celular. Qual a quantidade de alunos isso representa?
- Solução:
- Temos que o total de alunos entrevistados foi de 1.490 alunos, no qual, corresponde a 100%. Utilizando a regra de três e chamando de y a quantidade a ser encontrada, obtemos:
- 1.490 _____________________ 100%
- y ________________________ 56%
- Montando a proporção, temos:

- Aplicando a propriedade fundamental da proporção, ou seja,

- Logo, a quantidade de alunos que possuem celulares é de 835 alunos.
Esses problemas costumam aparecer nos vestibulares, por isso, dê uma atenção a eles!
Vamos verificar agora, que também podemos calcular problemas de valores com acréscimos ou descontos utilizando um fator de multiplicação, forma que dispensa a regra de três. Vamos conhecer?
Determinando os valores de acréscimos ou descontos pelo fator de multiplicação
O procedimento é bem simples, devemos calcular o fator de multiplicação, e, depois multiplicar a quantia inicial por esse fator, resultando no valor a ser determinado.
Para acréscimos, o fator de multiplicação é determinado pela seguinte fórmula:
fator = 1 + taxa de acréscimo (na forma decimal)
Já para decréscimos, o fator é da forma:
fator = 1 – taxa de desconto (na forma decimal)
Por exemplo, qual o aumento de 14% em R$ 112,00?
Solução:
- Vamos escrever 14% na forma de fração para depois determinarmos o mesmo na forma decimal.

- Calculando o fator de multiplicação obtemos:
- fator = 1 + 0,14 = 1,14
- Agora, basta multiplicarmos o fator pela quantia inicial, ou seja,
- 1,14 x 112,00= 127,68
- Portanto, o aumento é R$ 127,68.
De maneira análoga calculamos os valores de desconto, só lembrando que nosso fator de multiplicação será o de desconto.
Resumo gratuito de Regra de Três
Para complementar o seu entendimento sobre porcentagem, assista ao vídeo a seguir sobre Regra de Três
Gostou do resumo com o professor Vinni?
Exercícios de Cálculo de Porcentagem
1 – (Enem/2013) O contribuinte que vende mais de R$ 20 mil de ações em Bolsa de Valores em um mês deverá pagar Imposto de Renda. O pagamento para a Receita Federal consistirá em 15% do lucro obtido com a venda das ações.
Um contribuinte que vende por R$ 34 mil um lote de ações que custou R$ 26 mil terá de pagar de Imposto de Renda à Receita Federal o valor de:
a) R$ 900,00
b) R$ 1.200,00
c) R$ 2.100,00
d) R$ 3.900,00
e) R$ 5.100,00
2 – (PUC-RIO/2009) João recebeu um aumento de 10% e com isso seu salário chegou a R$1.320,00. O salário de João antes do aumento era igual a?
a) R$ 1.188,00
b) R$ 1.200,00
c) R$ 1.220,00
d) R$ 1.310,00
e) R$ 1.452,00
3 – (PUC-RIO/2007) 30% de 30% são:
a) 3000%
b) 300%
c) 900%
d) 9%
e) 0,3%
Gabarito
1 – b
2 – b
3 – d
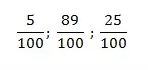 Os termos 5%, 89% e 25% são chamados de taxas percentuais.
Os termos 5%, 89% e 25% são chamados de taxas percentuais.
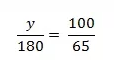 Aplicando a propriedade fundamental da proporção, segue a igualdade:
Aplicando a propriedade fundamental da proporção, segue a igualdade: