Você sabe qual é a relação existente entre ângulos, elementos de uma circunferência e o monumento Stonehenge, localizado no condado de Wiltshire na Inglaterra? E a relação entre o skatista Sandro dias com medidas de arcos? Venha explorar a circunferência trigonométrica para responder a estas e outras questões e deixar seus estudos em dia para o Enem!
Trigonometria: É provável que em anos anteriores você já tenha estudado as razões trigonométricas seno e cosseno associados a ângulos de triângulos. Em geral, nesse contexto, essas razões têm por objetivo determinar medidas de ângulos e lados dos triângulos.
Nesta aula, iremos estender o estudo da Trigonometria, tratando as razões seno, cosseno em uma circunferência. Para isto, vamos abordar tópicos como arcos e medidas de arcos em uma circunferência, a circunferência trigonométrica e redução ao primeiro quadrante.
A origem da trigonometria
Parece complicado? Então vamos dar um passo atrás, para revisar os ângulos na Circunferência, e depois mergulhar no mundo so Seno e do Cosseno. Confira agora um resumo com o professor Sérgio Sarkis,do canal do Curso Enem Gratuito.
As dicas do professor Sarkis:
- Veja no resumo acima um ponto muito importante ligado tanto à geometria, como à trigonometria: os ângulos.
- Vamos entender o que é um ângulo, como podemos medi-lo e, claro, vamos resolver alguns problema;
- Ângulo é a região formada entre duas semirretas que têm a mesma origem.
- A medida de um ângulo pode ser dada em grau ou em radiano. Um ângulo de 45º é o mesmo que um ângulo π/4 rad.
- A relação de conversão entre grau e radiano é: 180º – π rad. Veja exemplos de conversão na aula.
- Esse assunto aparece não só na prova de matemática, como também na de física.
- Acompanhe exercícios resolvidos sobre o cálculo do ângulo formado entre ponteiros de um relógio. Cuidado! Em horários como 2h10min, aparentemente os ponteiros da hora e do minuto ficam um sobre o outro, ou seja, não formam ângulo entre si.
- Porém, eles foram sim um ângulo, bem pequeno. Para calcular esse valor, o prof Sarkis te explica uma fórmula bem fácil!
Stonehenge
É possível que a trigonometria fosse utilizada inicialmente como instrumento prático, aplicada principalmente à Astronomia.
Ao que parece, foi essa ciência uma das primeiras a considerar a ideia de ângulos e associá-lo a elementos de uma circunferência como arcos e cordas. Uma das possíveis evidências dessa associação é Stonehenge, monumento da Idade de Bronze localizado no condado de Wiltshire, na Inglaterra.
Uma das possíveis evidências dessa associação é Stonehenge, monumento da Idade de Bronze localizado no condado de Wiltshire, na Inglaterra.
Stonehenge é um dos mais famosos círculos de pedras do mundo. Alguns historiadores acreditam que, no passado, esse local tenha sido utilizado para observações astronômicas.
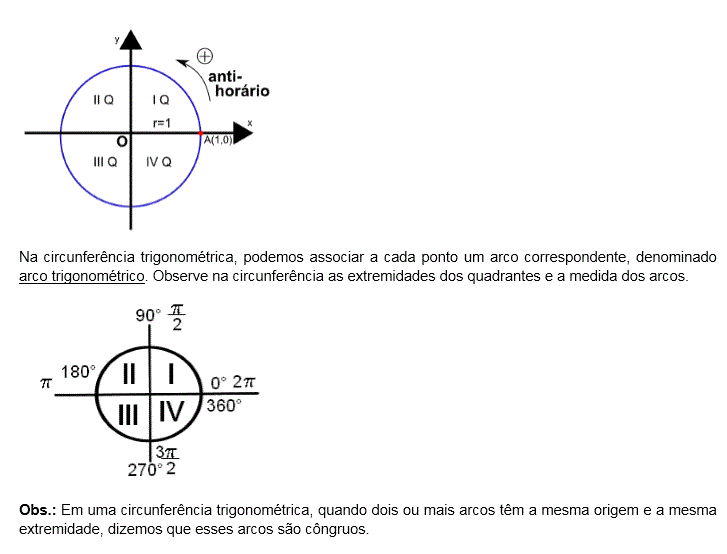
O Círculo Trigonométrico
Para resolver questões de trigonometria no Enem uma ferramenta muito útil para você é o Círculo Trigonométrico. Veja agora com o professor Lucar Borghesan como ele pode ajudar você.
O círculo trigonométrico, às vezes chamado também de ciclo trigonométrico é uma ferramenta importante no estudo da trigonometria e facilita muito a resolução de exercícios.
Veja as dicas do Círculo Trigonométrico:
- O ciclo trigonométrico é um círculo de raio 1. Ou seja, do seu cento até a borda, a medida é 1.
- Assim, podemos definir todos os valores de seno e cosseno que existem, uma vez que o círculo trigonométrico compreende todos os ângulos.
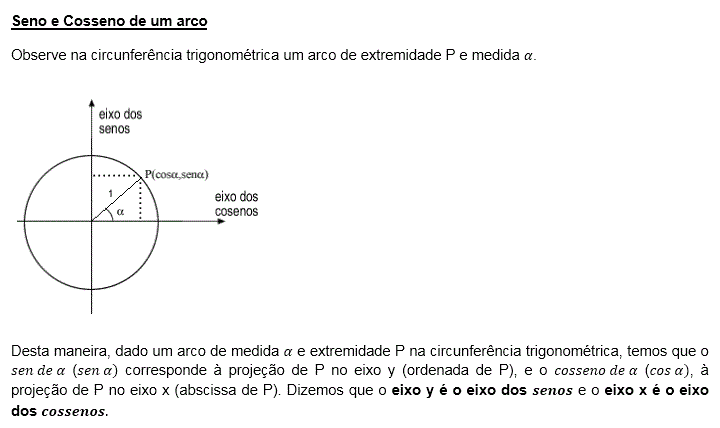
- Na trigonometria, seno e cosseno são chamados de razões trigonométricas. Para medir o valor do seno, é comum usar o eixo vertical do círculo trigonométrico.
- Desta forma, o eixo vertical do ciclo trigonométrico é chamado eixo dos senos. Por outro lado, podemos encontrar o valor do cosseno no eixo horizontal, de maneira que este é chamado de eixo dos cossenos.
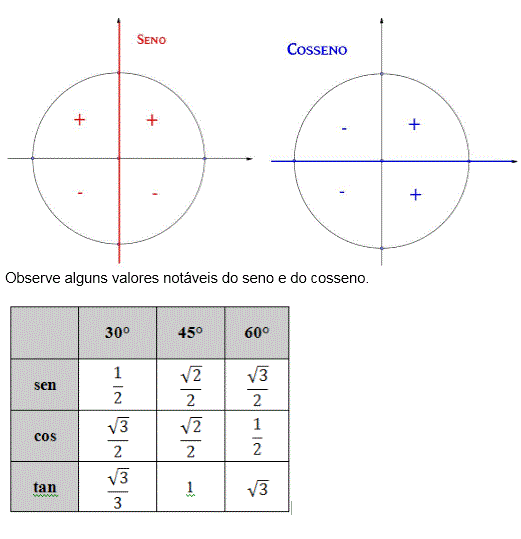
- Um exemplo muito legal de usar o círculo trigonométrico é conhecer também a tabela de ângulos notáveis, que traz os valores de seno, cosseno e tangente dos ângulos notáveis: 30º, 45º e 60º.
- Muitas vezes, o ângulo trabalhado em uma questão é diferente, mas, desenhando-o no círculo trigonométrico, verificamos que ele tem simetria com um dos ângulos notáveis.
- Desta maneira, já temos as razões trigonométricas, ou seja, o valor do seno, cosseno ou tangente pedido pelo exercício!
- Nesta aula acima o professor Lucas faz um resumo de como usar o círculo trigonométrico para encontrar seno, cosseno e tangente em questões de trigonometria, com exemplos de como isso cai nas provas e exercícios resolvidos.
Veja os Arcos na Trigonometria


Dica: É importante perceber que a medida de um arco não é o mesmo que o comprimento de um arco.
A medida depende exclusivamente do ângulo central correspondente enquanto que o comprimento equivale a sua medida linear, dependendo do comprimento do raio da circunferência.
A Circunferência Trigonométrica

Veja o que seria um giro de 900 graus
Ele já aconteceu numa prova de Skate. Confira agora:

A Determinação de Seno e Cosseno
Veja a Lei dos Senos com o professor Lucas Borguuesan, do Canal do Curso Enem Gratuito, com a dica para você dominar a regra básica.
A lei dos senos é usada quando temos um triângulo e sabemos os valores de dois ângulos e um lado. Quando temos os valores de dois lados e um ângulo, usamos a lei dos cossenos.
A lei dos senos diz o seguinte: se eu tenho um lado qualquer e divido pelo seno do ângulo que enxerga esse lado, isso é igual que um outro lado dividido pelo seno do seu ângulo. Ou seja, a fórmula da lei dos senos é: a / sen(A) = b / sen(B) = c / sen(C).
Para aplicar a lei dos senos, temos que definir qual ângulo está associado a qual lado para montar a fórmula. Para ficar mais fácil de visualizar, no vídeo, o professor Lucas faz uma demonstração de como aplicar a lei dos senos em um exercício!
Para aprender a usar a lei dos senos, o professor Lucas faz vários exercícios resolvidos de trigonometria mostrando como resolver questões de Matemática envolvendo a lei dos senos em um triângulo!
Veja Seno e Cosseno de um Arco
Veja a Lei do Cosseno
Confira as dicas do professor Lucas:
- A lei dos cossenos é usada quando temos um triângulo e só sabemos os valores de dois dos seus lados e o valor de um dos ângulos.
- Se for um triângulo retângulo, ou seja, um triângulo com um ângulo reto, seria possível resolver o problema com o Teorema de Pitágoras.
- Contudo, em outros tipos de retângulos é preciso aplicar a lei dos cossenos.
- A fórmula da lei dos cossenos, inclusive, é bastante parecida com o Teorema de Pitágoras, então é importante prestar atenção para não confundir as fórmulas.
- A fórmula da lei dos cossenos é a² = b² + c² – 2.b.c.cos(A)
- Na hora de aplicar a lei dos cossenos, lembre-se de que a “hipotenusa” é o lado oposto ao ângulo cujo valor é conhecido.
- Ou seja, o temos o valor do lado a e o valor do ângulo A, cujo cosseno precisamos descobrir caso o enunciado do exercício não informar.
- Veja na aula acima com o professor Lucas, que ele explica no quadro e faz os exercícios junto com você, para aprender de verdade.
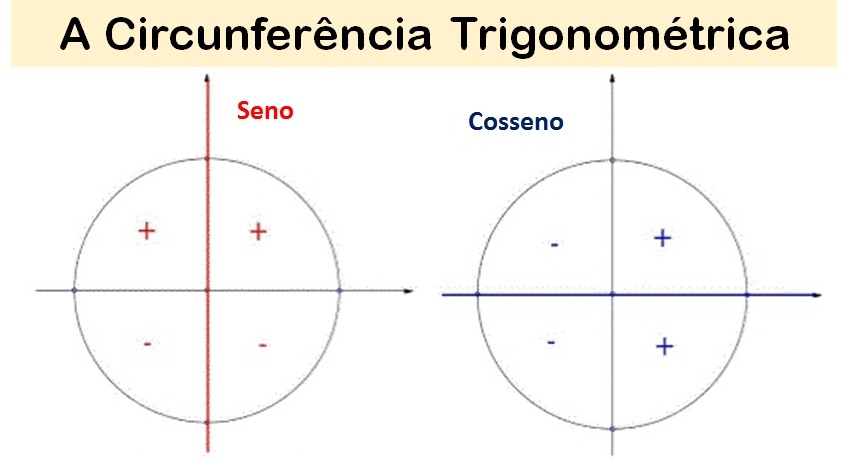
Sinais do seno e cosseno no ciclo trigonométrico

Se a aula está muito difícil para você compreender, é hora de fazer uma pausa didática e recapitular a origem a Trigonometria, e que está nas razões métricas dos triângulos. Veja no resumo com exercício resolvido.
Valeu pra você? Bora prosseguir, então!
E aí, curtiu o post? Agora, que tal testar seus conhecimentos?