Pertence, ou não Pertence ao Conjunto?- Está Contido, ou não está Contido? Que tal relembrar a relação de pertinência e as operações entre Conjuntos mandar bem na prova do Enem e nos vestibulares de todo Brasil? A professora Munique Dias preparou um super resumo para você. Cai direto. Não vacile!
O básico do básico em Matemática Enem: Quando um elemento está em um conjunto, dizemos que ele pertence a esse conjunto. Você sabe explicar esta relação, e a interseção entre conjuntos? Veja agora operações entre conjuntos
Nos conjuntos é possível estabelecer relações básicas como a de ‘Pertence’, quando o elemento ‘faz parte’; e a relação de ‘Não Pertence’, quando o elemento é estranho aos demais que formam o Conjunto. 
E, ainda, nas operações entre conjuntos é possível estabelecer a relação de ‘Interseção’, quando um determinado elemento ‘faz parte’ de dois ou mais conjuntos. Neste caso ele fica na ‘Interseção’, e ‘Pertence’ aos dois ou mais conjuntos considerados.
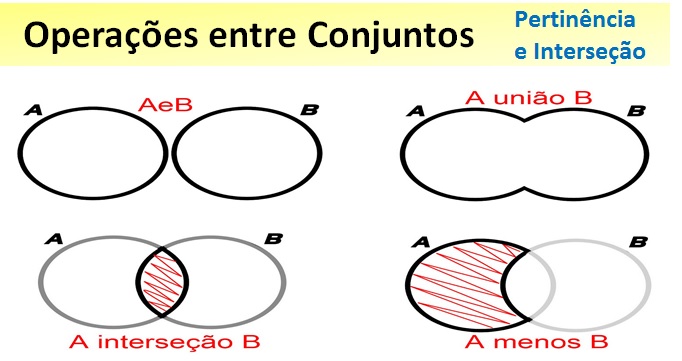
Operações entre Conjuntos
Veja neste exemplo: Considere o Conjunto ‘F’, onde F = {0, 2, 4, 6, 8,…}
Os símbolos utilizados para representar quando um elemento pertence ou não pertence a um determinado conjunto são: ∈ Pertence ∉ Não pertence. Para representar que elementos pertencem ou não ao conjunto ‘F’, veja a resolução a seguir do problema envolvendo Conjuntos:
- Resolução do Conjunto ‘F’:
- 2 ∈ F – lê-se que: 2 pertence a F.
3 ∉ F – lê-se que: 3 não pertence a F.
Confira as dicas no resumo básico sobre Conjuntos
Veja agora com o professor Lucas Borguesan, do canal do Curso Enem Gratuito, os macetes para você acertar as questões sobre Operações entre Conjuntos no Enem.
As dicas do professor Lucas:
- Quem nunca se confundiu na hora de fazer operações com conjuntos numéricos, não é mesmo?
- Muitas vezes, por se tratar de conjuntos de muitos elementos, alguns alunos podem se atrapalhar na hora de realizar as operações, como a União e a Intersecção.
- Realmente é preciso bastante atenção para não deixar nenhum elemento do conjunto numérico de lado na hora da operação.
- Mas, com um pouco de paciência, muito estudo e treinamento, pode aparecer qualquer conjunto numérico que você vai saber direitinho o que fazer com ele.
- Então, veja na aula acima como conhecer e dominar algumas dessas operações.
E quando for uma relação entre conjuntos?
Entre conjuntos, é errado usar a relação de pertinência. Assim, utilizamos as relações de inclusão.
- G = { 0, 1, 2, 3, 4, 5, 6, 7, …}
- O símbolo utilizado para representar quando um conjunto está contido ou não está contido em um determinado conjunto é:
- ⊂ Está contido
- ⊄ Não está contido
- F ⊂ G – lê-se: F está contido em G.
- G ⊄F- lê-se: G não está contido em F
- G ⊃F – lê-se: G contém F
Aprenda Operações entre conjuntos
Agora que você já estudou a relação de pertinência, que tal rever as operações entre conjuntos? Fique com a gente! –Existem algumas operações que podem ser realizadas entre conjuntos, são elas: intersecção, união e diferença.
Considerando os conjuntos A e B contidos num conjunto universo U, as operações entre eles podem ser representadas da seguinte maneira: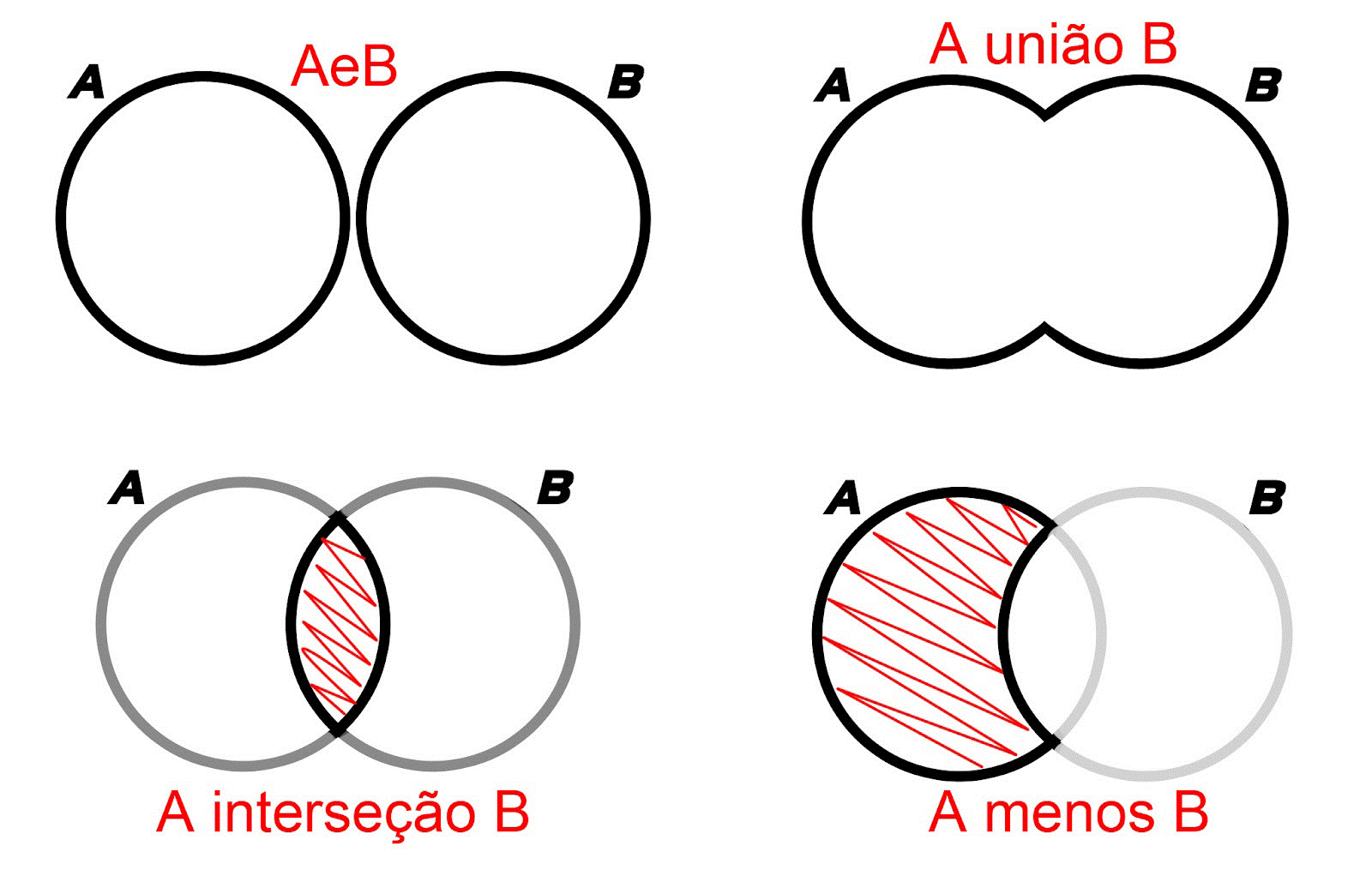
União
- A união de A com B é o conjunto formado por todos os elementos pertencentes a A e B.
- Notação: A U B lê-se A união com B.
A U B = {x / x Є A e x Є B}
Intersecção
- A intersecção de A com B é o conjunto formado pelos elementos comuns a A e B.
Notação: A ∩ B lê-se A intersecção com B.
A ∩ B = {x / x Є A e x Є B}
Diferença
- A diferença entre A e B é o conjunto formado pelos elementos que pertencem a A e não pertencem a B.
Notação: A – B lê-se A menos B
A – B = {x / x Є A e x B}
Complementar
- Dois conjuntos A e B, o complementar de B em A, designado por A∖B, é o conjunto cujos elementos são os elementos de A que não pertencem a B:
- Notação CAB lê-se complementar de B em relação a A.
- CAB = {x/x Є A e x ∉ B}
- Mas, fique ligado: É uma operação que só existe quando um conjunto está totalmente “dentro” do outro.
Inclusão e Pertinência – Veja aula gratuita
Confira agora com o professor Lucas como fazer inclusão e Pertinência nas operações entre Conjuntos. É pra gabaritar geral na matemática do Enem. Vem!
Dica 1 – O que mais cai em Matemática nos Vestibulares e no Enem? Veja aqui as melhores dicas: https://blogdoenem.com.br/category/cainaprova/matematica/
Dica 2 – Complemente os seus estudos para o Exame Nacional do Ensino Médio com esta aula de Regra de três simples que o Blog do Enem preparou para você. Não deixe de conferir! https://blogdoenem.com.br/teoria-dos-conjuntos-enem-vestibular/
Estude mais sobre as operações entre conjuntos assistindo a videoaula do Matemática do Aluno. Vamos lá! Cai no Enem e nos vestibulares de todo Brasil!
Você consegue resolver este exercício? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
(ESPM SP) Considere os seguintes subconjuntos de alunos de uma escola:
A: alunos com mais de 18 anos
B: alunos com mais de 25 anos
C: alunos com menos de 20 anos
Assinale a alternativa com o diagrama que melhor representa esses conjuntos
a)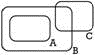 
b)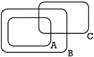 
c)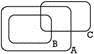 
d)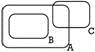 
e)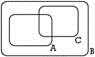 
Resposta: D
Dica 3 – Relembre outros assuntos de matemática acessando o nosso blog www.blogdoenem.com.br e gabarite as questões de matemática nas provas dos vestibulares e do Enem.
