Você lembra quais são os cinco Conjuntos Numéricos? é hora de rever os números Inteiros, Racionais, Irracionais, Reais e o conjunto dos números Naturais. É matemática básica. Vem!
Veja como aprender os Conjuntos Numéricos para a Matemática do Enem: os números são agrupados conforme suas características, esse agrupamento dá origem aos denominados Conjuntos Numéricos.
Mas o que é um conjunto numérico? Como aprender para a Matemática Enem? – Definimos por conjunto o agrupamento de termos com características parecidas, no caso da Matemática, os números são agrupados em conjuntos denominados numéricos. 
Quando esse conjunto é representado por extenso, escrevemos os números entre chaves { }, se o conjunto for infinito irá possuir incontáveis números, então o representamos com reticências.
Os cinco Conjuntos numéricos:
– Existem cinco conjuntos que são considerados fundamentais, por serem os mais utilizados em problemas e questões relacionados à matemática. Veja a seguir quais são esses conjuntos:
1 – Conjunto dos Números Naturais
- O Conjunto dos Números Naturais é representado pela letra maiúscula N e é formado por todos os números inteiros positivos incluindo o zero.
- Representação simbólica: N = {x є N/ x > 0} lê-se que x é um número pertencente ao conjunto dos números naturais, sendo que x é um número maior ou igual a zero.
- N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…}
- O símbolo (*) será utilizado para representar a exclusão do zero a qualquer conjunto, no caso dos números naturais temos:
- N* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…}
2 – Conjunto dos Números Inteiros
É representado pela maiúscula Z, e é formado pelos números inteiros negativos, positivos e o zero. Veja aqui : Z = {… -4, -3, -2, -1, 0, 1, 2, 3, 4,…}
O conjunto dos números Inteiros possui alguns subconjuntos:
- Z+= {0, 1, 2, 3, 4, 5, 6, 7, 8, …} Conjunto dos inteiros não negativos
- Z-={…, – 4, – 3, – 2, – 1, 0} Conjunto dos Inteiros não positivos
- Z*+= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…} Conjunto dos inteiros não negativos e não nulos (exclusão do zero).
- Z*–= {… – 5,- 4, – 3, – 2, – 1} Conjuntos dos inteiros não positivos, e não nulos.
.
Aula Gratuita sobre os Conjuntos Numéricos: Matemática Enem
Confira com os professores do Curso Enem Gratuito as dicas da hora para você dominar os Conjuntos Numéricos.
Muito bom o resumo. Bora continuar.
3 – Conjunto dos Números Racionais
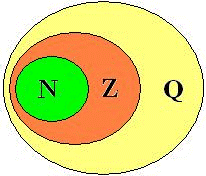
- Esse conjunto é representado pela letra maiúscula Q, sendo formado pela reunião dos conjuntos referentes aos números naturais e inteiros, portanto o conjunto N (naturais) e o Z (inteiros) estão inclusos no conjunto Q (racionais).
- A representação simbólica desse conjunto é:
- Q = {x = a/b, com a є Z e b є z*} lê-se x é um número racional obtido de uma divisão com números inteiros, em que o denominador no caso b deve ser diferente de zero.
- Q = {… – 2; – 1; 0; + ; + 1; +2, 14; + 4; + 4,555…}
Os termos numéricos que compõem o conjunto dos números racionais são:
- {+ 1, + 4} Números naturais.
- {- 2, -1, 0, + 1, + 4} Números inteiros.
- {1/2} Fração.
- {2,14) à Número decimal.
- { 4,555…} Dízima periódica.
4 – O Conjunto dos Números Irracionais
- Esse conjunto é representado pela letra maiúscula I, é formado pelos números decimais infinitos não periódicos, ou seja, números que possui muitas casas decimais, mas que não tem um período.
- O número PI que é igual a 3,14159265…
- Raízes não exatas como: = 1,4142135…
5 – O Conjunto os Números Reais
- Representado pela letra maiúscula R, compõem esse conjunto os números: naturais, inteiros, racionais e irracionais. Acompanhe o exemplo numérico a seguir:
- R = {… – 3,5679…; – 2; – 1; 0; + + 1; +2, 14; + 4; 4,555…; + 5; 6,12398…}
Então, podemos classificar os elementos do conjunto Q assim:
- {0, + 1, + 4} números naturais.
- {- 2, -1, 0, + 1, + 4, + 5} Números inteiros.
- {+ } fração.
- {+ 2,14) número decimal.
- {+ 4,555…} dízima periódica.
- {– 3,5679…; 6,12398…} números irracionais.
Dicas sobre os números reais para você não errar nas provas:
- N
Z Q R - Irracional = R-Q
- Q ∩ Irracional = Ø
- A soma e a multiplicação de dois números naturais têm como resultado um número natural;
- O oposto, ou simétrico de um número inteiro é também um número inteiro;
- Soma, subtração, multiplicação e divisão com denominador diferente de zero de dois números racionais é também um número racional;
- O inverso multiplicativo de um número racional nulo é um número racional;
- Se p é um número e q um número racional, então os números p,q + q, p/q e q/p são irracionais.
Z Enfim… Podemos representar o conjunto dos números naturais, inteiros, racionais e reais pelo seguinte diagrama: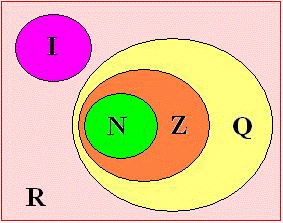 
Dica 2 – Pronto para gabaritar na prova de Matemática Enem? Faça uma revisão com esta aula sobre Razão, proporção e grandezas – https://blogdoenem.com.br/razoes-escalas-proporcoes-matematica/
Simulado Enem de Conjuntos
Teste o seu nível em 10 questões online. O Gabarito sai na hora, com aulas de reforço nas questões que você não acertar. Clique na imagem para ver o seu desempenho em Conjuntos para a Matemática do Enem > 
Dica 3 – Relembre outros assuntos de matemática acessando o nosso blog www.blogdoenem.com.br e gabarite as questões de matemática nas provas dos vestibulares e do Enem.
Você consegue resolver este exercício? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
(IFPE, 2015) Observando o número (–9,13571357135713…)2, é correto garantir que ele pertence ao conjunto:
a) N
b) Z
c) Q
d) I
e) R_
Resposta: C
