Que tal rever como se faz a transformação de números decimais em frações? É uma lógica simples para entender e nunca mais esquecer. E você utiliza no dia a dia sem perceber. Então preste bastante atenção, pois cai no Enem e no vestibular também!
Números Decimais e Frações. Revisão expressa para vestibular e Enem. Confira.
- Responde rápido:
- – Você concorda que 1/10 é a mesma coisa que 0,1?
- – Ou, então que 1/100 é o mesmo que 0,01?
- – E, concorda ainda que 1/1 é o mesmo que 1?
Então, estamos falando da transformação de Números Decimais para Frações, e vice-versa. É um conhecimento que se aplica em diversas situações do dia a dia, e também dos cálculos em Matemática.
É tema para questões do Exame Nacional de Ensino Médio, o Enem, e também para os vestibulares. E, dentro de casa, você encontra em coisas muito simples como uma receita de bolo, por exemplo.
Resumo de Frações e Números Decimais
Veja agora com o professor Lucas Borguesan, do canal do Curso Enem Gratuito, um resumo sobve como Transformar Frações em Números Decimais.
Viu só que não tem segredo. Agora, é colocar a mão na massa.
Veja este exemplo como fazer a transformação:
Se formos ao supermercado comprar 1 kg de batatas por R$ 1,32, e pagarmos a compra com uma nota de R$ 2,00, então receberemos R$ 0,68 de troco. Neste exemplo, podemos observar a utilização dos números decimais. Veja como transformar esses números decimais em frações:
- Decimais finitos: São aqueles que apresentam um número finito de casas decimais não nulas.
- Observe que:
- 1) 7/10 = 0,7
- 2) 7/100 = 0,07
- 3) 7/1000 = 0, 007
- 4) 216/100 = 2,16
Dica: Todo número cuja representação decimal for finita pode ser escrito na forma de uma fração com denominador 10, 100, 1000, etc.
O numerador da fração é o número inteiro que se obtém abandonando a vírgula, e o denominador é formado pelo número 1 acrescido de tantos zeros quanto forem as casas após a vírgula do número fornecido.
Dica do Blog do Enem – Estude também as operações envolvendo os números na forma decimal. Acesse aqui uma aula especial sobre Operações Decimais em Matemática. 
Veja o que são as Dízimas periódicas:
- Dízimas Periódicas s=São numerais decimais em que há repetição periódica e infinita de um ou mais algarismos.
- Observe as divisões:
- 1) 5/9 = 0,55555….
- 2) 32/99 = 0,32323232…
- 3) 121/999 = 0,121121121…
Note que estes números têm uma representação decimal infinita e periódica e são chamados de dízimas periódicas simples. A fração que os representa (Fração Geratriz) tem como denominador números 9.
Podemos estabelecer a seguinte regra para dízimas periódicas simples: o numerador da fração geratriz será o número do período e o denominador será 9 ou 99 ou 999, etc…, ou seja, será formado por tantos nove quanto forem os algarismos do período.
Exemplos:
1) 0,454545… = 45/99
2) 0,761576157615… = 7615/9999
3) 0,222222… = 2/9
E se o número for, por exemplo, 2,3222222…. ou 0, 43717171…?
Neste caso será chamado de dízima periódica composta e a sua transformação em fração pode ser feita da seguinte maneira:
Exemplos:
1) 2,3222222… =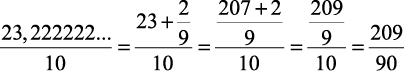 
2) 0,43717171… =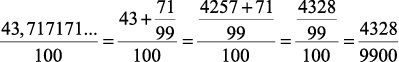 
Revise mais sobre a transformação dos números decimais em frações assistindo a videoaula. Nesse vídeo você aprende em apenas cinco minutos e vinte e cinco segundos, tudo sobre esse assunto bastante cobrado em diversas provas do Enem e dos vestibulares de todo Brasil. Não deixe essa chance passar!
- Que a matemática é tida como um monstro na vida da maioria dos(das) estudantes, principalmente de quem está se preparando para o vestibular e Enem, não é novidade.
- Mas, a parte divertida e que muitas vezes não é ensinada na sala de aula é a possibilidade de adaptação dos conteúdos.
- Um bom exemplo são os números decimais: tem estudantes que gostam mais de trabalhar com “números com vírgula” e outros que preferem trabalhar com frações.
- A mágica acontece quando você percebe que basta transformar números decimais em frações, ou vice e versa, para estudar da forma que você preferir.
- O mesmo quando falamos de porcentagem! Nesta aula acima veja como transformar números decimais em frações e em porcentagem
Dica de Matemática Enem – Revise aqui os Múltiplos e Divisores.
Você consegue resolver estes exercícios de matemática? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
questão) No tanque do seu carro cabem 50 litros de gasolina. Num certo momento, o marcador indica que ainda resta 1/4 do tanque. Se você quiser completar, quantos litros de gasolina deverá comprar? Se a gasolina custa R$2,58 o litro, quanto você pagará para completar o tanque?
Resposta: 37,5 litros e R$ 96,75 para completar o tanque.
