Acerte as questões básicas de Matemática nas provas para se garantir na pontuação e mandar bem no resultado. Veja resumo online de Mínimo Múltiplo Comum, e também de Máximo Divisor Comum. Cai sempre! Vem!
Você tem na ponta da língua e na ponta do lápis tudo o que já aprendeu sobre Mínimo Múltiplo Comum, Máximos Divisores, e Números Naturais? É hora de revisar para o Enem e o Vestibular. Com você, os Múltiplos e os Divisores!
Todos os conceitos que virão a seguir para você dominar Mínimo Múltiplo Comum e o Máximo Divisor Comum serão feitos dentro do universo dos números Naturais
Os Múltiplos
Os múltiplos de um número natural n são todos aqueles números cuja divisão por n é exata, ou seja, resto zero. Exemplo:
- ) Múltiplos de 3: M(3) = {0,3,6,9,12,15,…}
- ) Múltiplos de 7: M(7) = {0,7,14,21,28,…}
Os Divisores
Os divisores de um número natural n são todos aqueles pelos quais n pode ser dividido (divisão exata). Exemplo:
- ) Divisores de 12: D(12) = {1,2,3,4,6,12}
- ) Divisores de 7: D(7) = {1, 7}
Os Números primos
Veremos a seguir um conceito fundamental para o estudo dos múltiplos e divisores: os números Primos. Eles podem ser comparados aos alicerces de uma casa. Veremos que qualquer número natural pode ser escrito apenas com o uso deles.
Um número natural p é chamado de primo se ele admitir exatamente dois divisores: ele mesmo e o número 1. Exemplos:
- ) 2 é primo, pois é divisível apenas por 2 e por 1
- ) 7 é primo, pois é divisível apenas por 7 e por 1
- ) 9 não é primo, pois admite, além do próprio 9 e do 1, o número 3 como divisor.
Observação importante: O número 1 não é primo, pois admite apenas um divisor, o próprio número 1.
Os primeiros números primos são: 2,3,5,7,11,13,17,19,23,29,31,37,…
O conjunto dos números Primos é infinito. Isso foi provado pelo matemático grego Euclides (360 a.C. — 295 a.C.), considerado o pai da geometria.
Outro fato curioso acerca dos números primos é que à medida em que vão ficando maiores, também ficam mais “raros” . Atualmente, os primos tem uma importância muito grande numa área chamada Criptografia, ciência que estuda métodos de codificação e decodificação de mensagens, com muitas aplicações, por exemplo, em transações comerciais via internet.
Resumo sobre Números Primos
Assista à videoaula do prof. Lucas Borguesan, do canal do Curso Enem Gratuito, para aprofundar seus conhecimentos sobre números primos. Depois tem a aula sobre Mínimo Múltiplo Comum:
Dica 1 – Matemática Enem – Revise tudo sobre os números Naturais!
O Número Composto
Todo número Natural que não é primo é chamado de composto. Decorre desse conceito que todo número composto tem 3 ou mais divisores distintos.
Exemplo
12 é composto, pois admite os números 1, 2, 3, 4, 6, e 12 como divisores.
O Teorema Fundamental da Aritmética (fatoração única)
Todo número natural n>1 pode ser fatorado, de maneira única, através de potências onde as bases são números primos e os expoentes são números naturais não nulos.
Exemplos
1) 18 = 21.32 2) 8 = 23
3) 7350 = 21.31.52.72 4) 19 = 191
Mínimo Múltiplo Comum (MMC)
Observe o conjunto dos múltiplos de 6 e 8.
- M(6) = {0,6,12,18,24,,30,36,40,48,54,60,66,72,78,84,90,96, …}
- M(8) = {0,8,16,24,32,40,48,56,64,72,80,88,96,…}
- Os divisores comuns a 6 e 8 são: 0,24,48,72,96,…
Podemos concluir assim que o menor múltiplo comum (MMC) positivo de 6 e de 8 é 24.
Um modo mais prático de se obter o MMC é através da fatoração simultânea.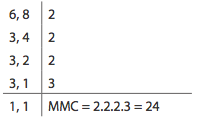
Resumo Especial de MMC
Para entender ainda melhor como fazer Mínimo Múltiplo Comum, veja a aula do prof. Lucas:
As dicas sobre Mínimo Múltiplo Comum
- O mínimo múltiplo comum tem inúmeras aplicações.
- Mas, geralmente utilizamos o MMC para adicionar ou subtrair frações com denominadores diferentes, não é mesmo?
- Só que não é só para isso que o MMC serve.
- Podemos resolver inúmeros problemas usando somente o processo de fatoração ou de múltiplos de um número.
- Para saber tudo sobre esse assunto, veja esta aula do professor Lucas. 🙂
Dica 2 – Matemática no Enem: domine as operações e o cálculo de juros
Máximo Divisor Comum (MDC)
Ilustraremos o conceito obtendo o MDC entre os números 36 e 120.
Os divisores de 36 e 120 são:
- D(36) = {1,2,3,4,6,9,12,18,36}
- D(120) = {1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120}
- Os divisores comuns são 1,2,3,4,6 e 12.
Logo, o maior divisor comum (MDC) vale 12.
Métodos práticos para obter o MDC
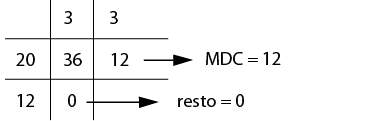
Método 1 – Fatoração simultânea
Usando novamente os números 36 e 120, temos:

Observe que os números circulados foram aqueles que dividiram simultaneamente 36 e 120. O MDC é o produto desses números circulados (divisores simultâneos).
MDC(36,120) = 2.2.3= 12
Método 2 – Método de Euclides (divisões sucessivas)
Novamente vamos usar como exemplo os números 36 e 120.
Começamos dividindo 120 por 36 e pondo em destaque o quociente e o resto.
A seguir, repetimos o processo, agora dividindo o número 36 pelo resto 12.
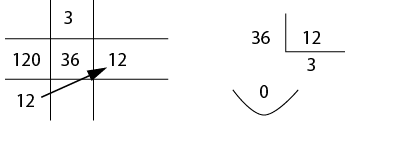
Quando chegamos no resto = 0, o MDC é o penúltimo resto obtido.
Teorema
O produto de dois números Naturais não nulos é igual ao produto entre o MDC e o MMC desses números.
a.b = MDC(a,b).MMC(a,b)
Exemplo
Os números 6 e 8 tem MDC = 2 e MMC = 24. Logo,
6.8 = MDC(6,8).MMC(6,8)
6.8 = 2.24
Dica 3 – Redação do Enem: Evite erros que podem fazer seu texto tirar nota zero
Exercício Resolvido
1) Numa estação rodoviária os ônibus para a cidade A partem de 6 em 6 horas e para a cidade B, de 8 em 8 horas. Numa ocasião, um ônibus para a cidade A partiu junto com outro para a cidade B. Qual o menor tempo possível para que isso aconteça de novo?
Gabarito: 24hs
2) Três rolos de barbante que medem, respectivamente, 24m, 84m e 90m, foram cortados em pedaços iguais e de maior comprimento possível. Então o comprimento de cada um desses pedaços vale:
Gabarito: 6m
Desafios sobr Mínimo Múltiplo Comum
Questão 1
Aline toma um comprimido de 4 em 4 horas e um xarope de 6 em 6 horas. Às 10 horas da manhã ele ingeriu os dois remédios. A que horas ela voltará a tomar os dois remédios juntos?
a) 16hs b) 18hs c)20hs d)22hs e) 24hs
Questão 2
(Enem 2005) Os números de identificação utilizados no cotidiano (de contas bancárias, de CPF, de Carteira de Identidade etc) usualmente possuem um dígito de verificação, normalmente representado após o hífen, como em 17326-9. Esse dígito adicional tem a finalidade de evitar erros no preenchimento ou digitação de documentos. Um dos métodos usados para gerar esse dígito utiliza os seguintes passos:
- multiplica-se o último algarismo do número por 1, o penúltimo por 2, o antepenúltimo por 1, e assim por diante, sempre alternando multiplicações por 1 e por 2.
- soma-se 1 a cada um dos resultados dessas multiplicações que for maior do que ou igual a 10.
- somam-se os resultados obtidos.
- calcula-se o resto da divisão dessa soma por 10, obtendo-se assim o dígito verificador.
O dígito de verificação fornecido pelo processo acima para o número 24685 é
a) 1. b) 2. c) 4. d) 6. e) 8.
Questão 3
(Enem 2ª aplicação 2010) Nosso calendário atual é embasado no antigo calendário romano, que, por sua vez, tinha como base as fases da lua. Os meses de janeiro, março, maio, julho, agosto, outubro e dezembro possuem 31 dias, e os demais, com exceção de fevereiro, possuem 30 dias. O dia 31 de março de certo ano ocorreu em uma terça-feira.
Nesse mesmo ano, qual dia da semana será o dia 12 de outubro?
a) Domingo. b) Segunda-feira. c) Terça-feira. d) Quinta-feira. e) Sexta-feira.
Questão 4
Três rolos de barbante que medem, respectivamente, 24m, 84m e 90m, foram cortados em pedaços iguais e de maior comprimento possível. Então o comprimento de cada um desses pedaços vale:
a) 6 b) 12 c) 14 d) 18 e) 24
Questão 5
(G1 – cps 2010) Pensando em contribuir com uma alimentação mais saudável para a sua família, o Sr. João está planejando uma horta em um espaço retangular de 1,56 m por 84 cm, disponível em seu quintal.
Ele inicia o preparo da horta dividindo o comprimento e a largura do terreno em partes iguais, todas de mesma medida inteira, quando expressas em centímetros.
Dessa maneira, o Sr. João formou, na superfície do terreno, um quadriculado composto por quadrados congruentes de modo que as medidas das arestas de cada quadrado tivessem o maior valor possível.Sua intenção é plantar, no centro de cada quadrado obtido, uma única muda.

Nessas condições, a quantidade máxima de mudas que pode ser plantada é
a) 54. b) 76. c) 91. d) 120. e) 144.
Você consegue solucionar estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
Texto Complementar
Novos números primos gigantes são anunciados
Concurso quer premiar interessados em descobrir um número primo com pelo menos 10 milhões de dígitos
por John Matson
Concurso quer premiar interessados em descobrir um número primo com pelo menos 10 milhões de dígitos. O prêmio pode ser ainda maior para quem encontrar um primo com 100 milhões de dígitos.
Números primos sempre tiveram um apelo especial para os amantes da matemática, desde o astrônomo grego Eratóstenes, que desenvolveu um método para encontrar números primos, há 2.200 anos, até os criptógrafos de hoje, que fizeram deles a base dos protocolos modernos de criptografia. Números primos, divisíveis somente por um e por eles mesmos, têm até sido disputados como direito de propriedade numérica: Roger Schlafly, consultor de informática da Califórnia, patenteou dois números primos em 1994.
O consórcio que descobriu os seis maiores números primos conhecidos está prestes a revelar mais dois – incluindo, talvez, um gigante ganhador de um prêmio de US$ 100 mil.
Descobertas preliminares foram noticiadas em outubro. O concurso, denominado Grande Busca pelo Primo Mersenne na Internet (GIMPS em inglês), teve início em 1996 e procura números primos do tipo 2n – 1, conhecidos como primos de Mersenne, dos quais 44 já foram identificados (as novas descobertas seriam as de números 45 e 46).
A busca, utilizando recursos de centenas de computadores em todo o mundo, é lenta. Segundo a GIMPS, os testes com apenas um número, usando um Pentium 4, de 2 GHz pode levar dois meses. Portanto, pode-se comemorar, depois de dois anos sem novidades, a descoberta quase simultânea de dois primos de Mersenne – um no dia 23 de agosto e outro no dia 6 de setembro.
Há uma boa chance de que um desses recém-nascidos primos concorra ao prêmio de US$ 100 mil da Electronic Frontier Foundation, que será oferecido ao descobridor de um número primo com pelo menos 10 milhões de dígitos. O recorde atual, o número 232582657 – 1, descoberto em 2006, não se qualificou porque tem apenas 9.808.358 dígitos.
De qualquer forma, os novos números certamente ficarão entre os sete maiores de todos os números primos conhecidos. Já foi demonstrado que os primos de Mersenne menores que pa o sexto lugar do ranking são todos conhecidos. Qualquer que seja o resultado, a GIMPS oferecerá um prêmio ainda maior, de US$ 150 mil, para quem descobrir um número primo de 100 milhões de dígitos ou mais.
Fonte: www2.uol.com.br Resumo de MMC Mínimo Múltiplo Comum


