Entenda o que é módulo de um número e função modular

Neste post você aprenderá a definição de módulo de um número real e a definição de função modular, assim como o seu gráfico e as equações modulares e suas resoluções.

O que é um módulo

Podemos dizer que módulo é o mesmo que distância de um número real ao número zero. O módulo de um número real surgiu da necessidade de medir a distância de um número negativo ao zero.

Ao medirmos a distância de um número negativo qualquer ao zero, percebe-se que a distância fica negativa. Como não é usual dizer que uma distância ou comprimento é negativo, foi criado o módulo de número real, que torna o valor positivo ou nulo.

Assim, podemos dizer que o módulo de um número real irá seguir duas opções:

• O módulo ou valor absoluto de um número real é o próprio número, se ele for positivo.
• O módulo ou valor absoluto de um número real será o seu simétrico, se ele for negativo.

O símbolo de um módulo ou valor absoluto de um número real é feito por duas barras paralelas:

|x| = x, se x ≥ 0, e -x, se x < 0 

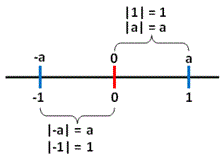
Dessa forma, representamos da mesma forma o módulo de um número positivo e de um número negativo. Por exemplo: |1| pode ser 1 ou -1. Isso ocorre porque a distância de -1 até o zero e de 1 até o zero é a mesma. Observe na reta numérica abaixo:

Função Modular

Dependendo dos valores de x, uma função f pode ser definida por duas ou mais sentenças. Como exemplo, podemos ter uma função de IR em IR definida por:

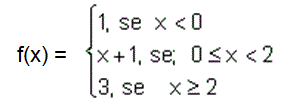
A função modular apresenta a característica de valor absoluto. Isto é, o que está em modulo é considerado em valor absoluto e, consequentemente, sem sinal. Portanto, define-se módulo ou valor absoluto de x e indica-se por |x|.

Uma função é modular se a cada x associa |x|, f(x) = |x|, onde: |x| =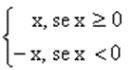

Portanto, a função modular pode ser transformada em duas possibilidades, a saber: quando a função que está no módulo for positiva, ela permanece como está, e quando a função que está no módulo for negativa, troca-se o sinal da função.

NOTA: O domínio dessa função f são todos os reais e a imagem [0, ∞] ou simplesmente: D(f) = IR e Im(f) = IR₊.

Obs: √x² = |x|

O gráfico de uma função modular pode ser esboçado mediante a separação em sentenças, isto é, dada a função f(x) = |x-1|, vamos transformá-la em uma função determinada por mais de uma sentença. Estudando o sinal da função que está no módulo, ou seja, achando a raiz da função que está no módulo, x – 1 = 0 e, portanto, x = 1. Logo, temos

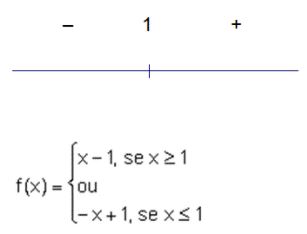
Basta atribuir valores convenientes a x e verificar a imagem em f(x). Fazendo isso obteremos pontos que determinam o traçado do gráfico. Observe a tabela em seguida:

X	-1	0	1	2
Y	2	1	0	1

Equações modulares

Nas equações modulares usa-se a mesma ideia, isto é, o que está em módulo ou é positivo ou é negativo, e isto pode ser alterado multiplicando-se a equação negativa por  –1.

Exemplos de equações modulares

Exemplo 1: | x – 2 | = 3

Temos, então, duas opções:

x – 2 = 3 ou -(x-2) = 3 ⇒ x – 2 = -3

Então:

x = 3 + 2  = 5 ou x = -3 + 2 = -1

S = {-1, 5}

Exemplo 2: |2x + 4| > 2

Resolver a equação |2x + 4| > 2 é equivalente a resolver as equações 2x + 4 > 2 ou 2x + 4 < -2. Na primeira equação tem-se x > -1 e na segunda equação tem-se x < -3. Portanto, a solução é a união entre as duas respostas, ou seja, S = {x ∈ IR; x < -3 ou x > -1}.

Exemplo 3: |3x + 9| ≤ 6

Resolver a equação |3x + 9| ≤ 6 é o mesmo que resolver 3x + 9 ≤ 6 e 3x + 9 ≥ -6. Portanto, na primeira tem-se x ≤ -1 e na segunda tem-se x ≥ -5. Assim, a solução é a intersecção, ou seja, S = {x ∈ IR; -5 ≤ x ≤ -1 }.

Resumo sobre módulo e função modular

Para entender melhor o conteúdo de módulo e função modular, assista à videoaula com o prof. Lucas do canal do Curso Enem Gratuito e, em seguida, resolva os exercícios:

Exercícios sobre módulo e função modular

1 – (ESPCEX/2018)    

Sabendo que o gráfico a seguir representa a função real f(x) = |x – 2| + |x + 3|, então o valor de a + b + c é igual a

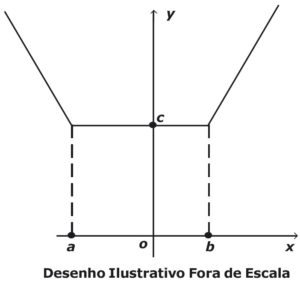
a) –7.

b) –6.

c) 4.

d) 6.

e) 10.

2 – (UDESC SC/2017)    

Considerando a função f(x) = |x²-1| e os conjuntos  A= {x ∈ R / x < 0} e B = [-1, 2], é correto afirmar que:

a) f(A∩B) = f(A) ∩ f(B)

b) f(A – B) = f(A) – f(B)

c) f(B – A)⊂ f(B) – f(A)

d) f(B^C) = (f(B))^C

e) f(A∪B) = f(A)∪f(B)

3 – (UNIFAP AP/2015)    

Ezequiel e Marta têm dificuldades para resolver problemas que envolvam funções modulares. Daí escolhem a seguinte questão para treinar:

Sendo f(x) = |2x + 1|, qual é o valor de x quando f(x) = 2.

Desta forma, qual foi à solução correta que eles encontraram:

a) -3/2 e 1/2

b) 1 e 2

c) 3/2 e 1/2

d) 3/2 e -1/2

e) 1

4 – (UFTM/2010)    

A função f(x) = |x + 3| – |x + 1| tem valor maior que zero, para x real obedecendo à condição

a) x < –3.

b) –3 < x < 3.

c) x > 3.

d) x < 2.

e) x > –2.

GABARITO: 

1. C
2. E
3. A
4. E