Definições e propriedades dos Polinômios – Matemática Enem & Encceja

O básico do básico você já sabe, mas não custa lembrar: polinômio é uma expressão algébrica composta por dois ou mais monômios.   Mas, esta é a definição escrita. Na Matemática sempre temos a representação da equação.

Veja a seguir que podemos definir como equação polinomial toda equação escrita na forma:

Veja o que é o Grau de um polinômio:  O grau de um termo de uma variável em um polinômio é o expoente dessa variável nesse termo.   Por exemplo, em 2x³ + 4x² + x + 7, o termo de maior grau é 2x³; esse termo, e portanto todo o polinômio, é dito ser de grau 3.

Polinômios Idênticos: São polinômios de mesmo grau, que possuem os coeficientes correspondentes iguais.

Veja as Operações fundamentais: Adição e Subtração

• Considere os dois polinômios a seguir:
• –2x² + 5x – 2   e   –3x³ + 2x – 1.
• Agora, vamos efetuar a adição e a subtração entre eles.

 

• Adição:  (–2x² + 5x – 2) + (–3x³ + 2x – 1)
• O Básico, você lembra? vamos eliminar os parênteses,  realizando o jogo de sinal. Acompanhe:
•  –2x² + 5x – 2 – 3x³ + 2x – 1
• Agora é a etapa de reduzir os termos semelhantes. Veja:
•  –2x² + 7x – 3x³ – 3
• Próximo passo: ordenar de forma decrescente de acordo com a potência. Vamos lá!
•  –3x³ – 2x² + 7x – 3

 

Dica 2 – Estude para o Exame Nacional do Ensino Médio com esta aula de Funções Polinomiais de 2º grau para a prova de Matemática Enem – https://blogdoenem.com.br/funcao-polinomial-2o-grau-matematica-enem/

Subtração de Polinômios:

• (–2x² + 5x – 2) – (–3x³ + 2x – 1)
• eliminar os parênteses realizando o jogo de sinal
•  –2x² + 5x – 2 + 3x³ – 2x + 1
• reduzir os termos semelhantes
•  –2x² + 3x – 1 + 3x³
• ordenar de forma decrescente de acordo com a potência
• 3x³ – 2x² + 3x – 1

 

 Multiplicação de polinômio por polinômio

Para efetuarmos a multiplicação de polinômio por polinômio devemos utilizar a propriedade distributiva.

• Veja neste exemplo:
•  (x – 1) * (x2 + 2x – 6)
• x.x2 + x.2x – x.6 + (-1).x2 + (-1).2x – (-1).6
•  x³ +2x² – 6x – x² – 2x + 6
• reduzindo os termos semelhantes.
•  x³ + x² – 8x + 6

Dica do Blog – Confira com o professor Sérgio Sarkis, do canal Curso Enem Gratuito,  aulas de Matemática Enem para revisar Equação Polinomial do 1º grau e do 2º grau. Aprenda a resolver esses problemas no Enem e no Encceja.

Aula Gratuita: Equação do 1º grau

.

Agora, aula gratuita para resolver Equações do 2º grau

Valeu pra você? Bora seguir com a Divisão dos Polinômios.

Divisão de polinômios

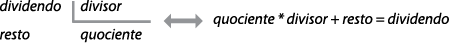
 Vamos dividir um polinômio por um monômio, com o intuito de entendermos o processo operatório. Observe:

 Exemplo

Continue aprendendo com nosso professor. Após assistir, revise o que você aprendeu respondendo aos nossos desafios!

 

Desafios

Questão 1

Quais são os polinômios que representem o quociente q(x) e o resto r(x) da divisão do polinômio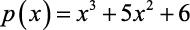

pelo polinômio ?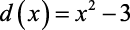

a)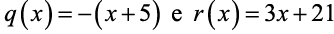

b)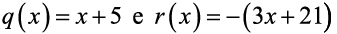

c)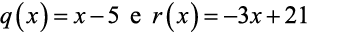

d)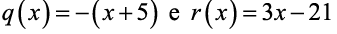

e)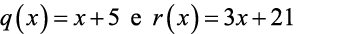 

 

Questão 2

Dados dois polinômios A(x) e B(x), sabe-se que S(x)=A(x)+B(x) é um polinômio de grau 8 e que D(x)=A(x)-B(x) é um polinômio de grau 5. É correto afirmar:

a) O polinômio W(x)=B(x)-A(x) tem grau 8.

b) Os polinômios A(x) e B(x) têm o mesmo grau.

c) O polinômio C(x)=A(x).B(x) tem grau 13.

d) O polinômio A(x) tem grau 5.

e) O grau do polinômio B(x) é menor que 7.

Questão 3

O polinômio 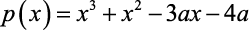é divisível pelo polinômio 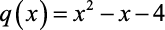. Qual o valor de a?

a) a=-2

b) a=-1

c) a=0

d) a=1

e) a=2

Se os polinômios

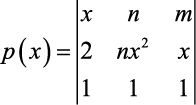        e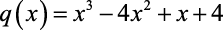      

 são idênticos, então o valor de é:

a) 2

b) 3

c) 4

d) 5

Questão 5

Para que os polinômios

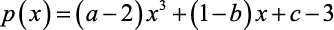e

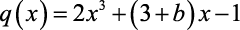
 sejam idênticos, os valores de a, b e c devem ser, respectivamente:

a) -4, -1 e 2

b) -4, 1 e -2

c) 4, -1 e 2

d) 4, 1 e 2