Revise o que você aprendeu sobre Estatística para mandar bem nas provas. Cai direto, e muita gente se perde na hora de calcular a Média Simples, a Média Ponderada, ou a Mediana. Mas, é bem mais simples do que parece.Veja nesta aula com dicas, exemplos e exercícios sobre o conteúdo. Estude com a gente para gabaritar Matemática.
Estatística cai direto no Enem, no Encceja e no Vestibular. E, para a vida moderna, saber calcular rapidamente probabilidades e estatísticas é uma competência demandada pelo mercado de trabalho.
Podemos entender a Estatística como sendo o método de estudo de comportamento coletivo, cujas conclusões são traduzidas em resultados numéricos. Podemos, intuitivamente, dizer que Estatística é uma forma de traduzir o comportamento coletivo em números.
- Universo Estatístico ou População Estatística: Conjunto formado por todos os elementos que possam oferecer dados pertinentes ao assunto em questão.
- Amostra: É um subconjunto da população estatística. Quando o Universo Estatístico é muito vasto ou quando não é possível coletar dados de todos os seus elementos, retira-se desse universo um subconjunto chamado amostra. Os dados são coletados dessa amostra.
- Rol: É toda sequência de dados numéricos colocados em ordem decrescente ou crescente.
Medidas de Tendência Central
As medidas de tendência central são utilizadas quando é necessário representar um conjunto de dados, obtidos em uma pesquisa, por meio de um único valor. Essas medidas indicam que os dados tendem a concentrar-se em torno deste valor.
A média aritmética simples também é conhecida apenas por média. É a medida de posição mais utilizada e a mais intuitiva de todas. Ela está tão presente em nosso dia-a-dia que qualquer pessoa entende seu significado e a utiliza com frequência.
A média aritmética de um conjunto de valores numéricos é calculada somando-se todos estes valores e dividindo-se o resultado pelo número de elementos somados, que é igual ao número de elementos do conjunto, ou seja, a média de n números é sua soma dividida por n.
Considere a seguinte situação:
A tabela abaixo mostra as notas de matemática de um aluno em um determinado ano: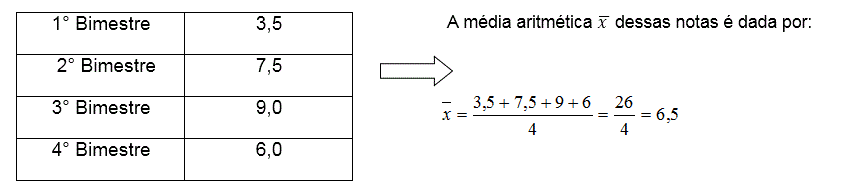
Ou seja; calcular uma média aritmética significa calcular o quociente (divisão) entre a soma de todos os elementos pela quantidade de elementos obtidos.
Obs.: (Interpretação do resultado) Ter média 6,5 significa dizer que, apesar de ele ter obtido notas mais altas ou mais baixas em outros bimestres, a soma das notas (26) é a mesma que ele alcançaria se tivesse obtido nota 6,5 em todos os bimestres.
Aula Gratuita de Estatística
Veja com o professor Sérgio, do Canal Curso Enem Gratuito, uma aula com a síntese do que você precisa saber para resolver as questões de Estatísticas no Enem, no Encceja e nos Vestibulares. Confira a Média Simples, a Média Ponderada, e a Mediana:
Gostou da aula do professor Sérgio? Viu como ele explica de maneira bem prática para você compreender, e depois conseguir resolver as questões? Bora adiante, para aprender um pouco mais.
Nos cálculos envolvendo média aritmética simples, todas as ocorrências têm exatamente a mesma importância ou o mesmo peso. Dizemos então que elas têm o mesmo peso relativo. No entanto, existem casos onde as ocorrências têm importância relativa diferente. Nestes casos, o cálculo da média deve levar em conta esta importância relativa ou peso relativo. Este tipo de média chama-se média ponderada.
Ponderar é sinônimo de pesar. No cálculo da média ponderada, multiplicamos cada valor do conjunto por seu “peso”, isto é, sua importância relativa.
Considere a seguinte situação:
Cinco baldes contêm 4 litros de água cada um, três outros 2 litros de água, cada um e, ainda, dois outros contém 5 litros de água, cada um. Se toda essa água fosse distribuída igualmente em cada um dos baldes, com quantos litros ficaria cada um?
Solução:
A quantidade de litros que ficaria em cada balde é a média aritmética ponderada:
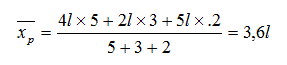
Ou seja, a quantidade, em litros, de água em cada balde é chamada de média ponderada dos valores 4 litros, 2 litros e 5 litros, com pesos 5; 3 e 2.
Exemplo (Média aritmética e ponderada)
As médias escolares podem ser calculadas por meio das médias simples. Se para passar de ano, você precisa tirar média 7, e a média é calculada com quatro provas, precisaremos pegar as notas que tirou em todas as provas, e dividir por quatro, que é o número de avaliações realizadas. Na primeira prova você tirou 8, na segunda tirou 7, na outra tirou 6 e na última tirou 7. Partimos então para o cálculo:
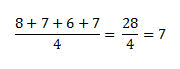
Sua média, nesse caso, seria 7 e você estaria aprovado.
Usando o mesmo exemplo da nota escolar, imagine que cada uma das notas tem um peso distinto. A primeira prova, possuía peso 2, a segunda peso 2, a terceira peso 3 e a quarta peso 3. Como isso pode ser calculado? Multiplica-se o valor pelo seu peso, somando aos resultados das outras multiplicações e então divide-se pela soma de todos os pesos. Confira o cálculo do exemplo:
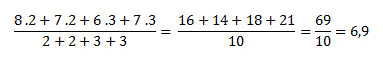
Nesse caso, a média seria 6,9.
Na média ponderada, ao contrário da média simples, a alteração da posição dos números pode ocasionar em resultados errados. Se você errasse, por exemplo, aplicando peso 1 às duas primeiras notas e peso 2 às seguintes, sua média seria diferente:
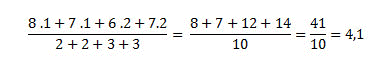
Isso faria bastante diferença, certo? Lembre-se sempre de fazer a multiplicação dos pesos com cada um dos valores antes de somá-los e de conferir se os pesos estão aplicados ao valor correto. Gostou da revisão?
Confira nestas questões e na aula gratuita abaixo como está o seu cérebro para a Estatística!
São nove questões de vestibulares e de padrão Enem para você vencer os seus limites. E tem ainda uma aula em vídeo gratuita para você revisar o que já tiver esquecido. Vamos lá!
Questão 01
(Ulbra 2012) Preocupada com a sua locadora, Marla aplicou uma pesquisa com um grupo de 200 clientes escolhidos de forma aleatória, sobre a quantidade de filmes que estes locaram no primeiro semestre de 2011. Os dados coletados estão apresentados na tabela a seguir:
|
Número de filmes alugados |
|
|
Número de filmes |
Frequência |
|
0 |
25 |
|
1 |
30 |
|
2 |
55 |
|
3 |
90 |
|
Total |
200 |
A média, a moda e a mediana destes dados são, respectivamente, os seguintes:
a) 2,05; 3; 2.
b) 1,5; 2; 3.
c) 1,5; 3; 3.
d) 1,5; 3; 2.
e) 2,05; 2; 3.
Dica 1 – Relembre tudo sobre Estatística em mais esta aula de revisão para a prova de Matemática Enem. Estude com a gente para o Exame Nacional do Ensino Médio! – https://blogdoenem.com.br/estatistica-matematica-enem/
Questão 02
(Enem 2011) Uma enquete, realizada em março de 2010, perguntava aos internautas se eles acreditavam que as atividades humanas provocam o aquecimento global. Eram três alternativas possíveis e 279 internautas responderam à enquete, como mostra o gráfico.
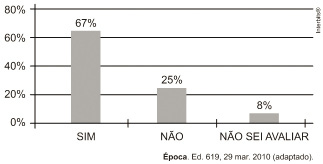
Analisando os dados do gráfico, quantos internautas responderam “Não” à enquete?
a) Menos de 23.
b) Mais de 23 e menos de 25.
c) Mais de 50 e menos de 75.
d) Mais de 100 e menos de 190.
e) Mais de 200.
Dica 2 – Relembre sobre Probabilidade nesta aula de revisão para a prova de Matemática Enem. Estude com a gente para o Exame Nacional do Ensino Médio! – https://blogdoenem.com.br/probabilidade-matematica-enem/
Questão 03
(Enem 2ª aplicação 2010) Em uma corrida de regularidade, a equipe campeã é aquela em que o tempo dos participantes mais se aproxima do tempo fornecido pelos organizadores em cada etapa. Um campeonato foi organizado em 5 etapas, e o tempo médio de prova indicado pelos organizadores foi de 45 minutos por prova. No quadro, estão representados os dados estatísticos das cinco equipes mais bem classificadas
Dados estatísticos das equipes mais bem classificadas (em minutos)
|
Equipes |
Média |
Moda |
Desvio-Padrão |
|
Equipe I |
45 |
40 |
5 |
|
Equipe II |
45 |
41 |
4 |
|
Equipe III |
45 |
44 |
1 |
|
Equipe IV |
45 |
44 |
3 |
|
Equipe V |
45 |
47 |
2 |
Utilizando os dados estatísticos do quadro, a campeã foi a equipe
a) I.
b) II.
c) III.
d) IV.
e) V.
Dica 3 – Que tal revisar sobre Análise Combinatória? Aproveite esta aula e fique preparado para a prova de Matemática Enem. Estude com a gente para o Exame! – https://blogdoenem.com.br/analise-combinatoria-1-matematica-enem/
Questão 04
(Enem 2010) Marco e Paulo foram classificados em um concurso. Para a classificação no concurso o candidato deveria obter média aritmética na pontuação igual ou superior a 14. Em caso de empate na média, o desempate seria em favor da pontuação mais regular. No quadro a seguir são apresentados os pontos obtidos nas provas de Matemática, Português e Conhecimentos Gerais, a média, a mediana e o desvio padrão dos dois candidatos.
Dados dos candidatos no concurso
|
Matemática |
Português |
Conhecimentos Gerais |
Média |
Mediana |
Desvio Padrão |
|
|
Marco |
14 |
15 |
16 |
15 |
15 |
0,32 |
|
Paulo |
8 |
19 |
18 |
15 |
18 |
4,97 |
O candidato com pontuação mais regular, portanto mais bem classificado no concurso, é
a) Marco, pois a média e a mediana são iguais.
b) Marco, pois obteve menor desvio padrão.
c) Paulo, pois obteve a maior pontuação da tabela, 19 em Português
d) Paulo, pois obteve maior mediana.
e) Paulo, pois obteve maior desvio padrão.
Questão 05
(Enem 2ª aplicação 2010) O gráfico expõe alguns números da gripe A-H1N1. Entre as categorias que estão em processo de imunização, uma já está completamente imunizada, a dos trabalhadores da saúde.
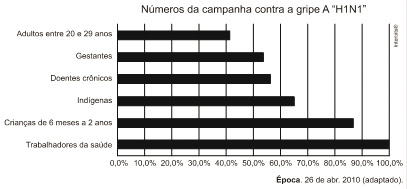
De acordo com o gráfico, entre as demais categorias, a que está mais exposta ao vírus da gripe A-H1N1 é a categoria de
a) indígenas.
b) gestantes.
c) doentes crônicos.
d) adultos entre 20 e 29 anos.
e) crianças de 6 meses a 2 anos.
Questão 06
(Enem 2009) Suponha que a etapa final de uma gincana escolar consista em um desafio de conhecimentos. Cada equipe escolheria 10 alunos para realizar uma prova objetiva, e a pontuação da equipe seria dada pela mediana das notas obtidas pelos alunos. As provas valiam, no máximo, 10 pontos cada. Ao final, a vencedora foi a equipe Ômega, com 7,8 pontos, seguida pela equipe Delta, com 7,6 pontos. Um dos alunos da equipe Gama, a qual ficou na terceira e última colocação, não pôde comparecer, tendo recebido nota zero na prova. As notas obtidas pelos 10 alunos da equipe Gama foram 10; 6,5; 8; 10; 7; 6,5; 7; 8; 6; 0.
Se o aluno da equipe Gama que faltou tivesse comparecido, essa equipe
a) teria a pontuação igual a 6,5 se ele obtivesse nota 0.
b) seria a vencedora se ele obtivesse nota 10.
c) seria a segunda colocada se ele obtivesse nota 8.
d) permaneceria na terceira posição, independentemente da nota obtida pelo aluno.
e) empataria com a equipe Ômega na primeira colocação se o aluno obtivesse nota 9.
Questão 07
(Enem cancelado 2009) Depois de jogar um dado em forma de cubo e de faces numeradas de 1 a 6, por 10 vezes consecutivas, e anotar o número obtido em cada jogada, construiu-se a seguinte tabela de distribuição de frequências.
|
Número obtido |
Frequência |
|
1 |
4 |
|
2 |
1 |
|
4 |
2 |
|
5 |
2 |
|
5 |
1 |
A média, mediana e moda dessa distribuição de frequências são, respectivamente
a) 3, 2 e 1
b) 3, 3 e 1
c) 3, 4 e 2
d) 5, 4 e 2
e) 6, 2 e 4
Questão 08
(Enem 2005) A escolaridade dos jogadores de futebol nos grandes centros é maior do que se imagina, como mostra a pesquisa a seguir, realizada com os jogadores profissionais dos quatro principais clubes de futebol do Rio de Janeiro.
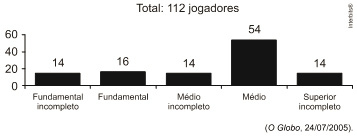
De acordo com esses dados, o percentual dos jogadores dos quatro clubes que concluíram o Ensino Médio é de aproximadamente:
a) 14%.
b) 48%.
c) 54%.
d) 60%.
e) 68%.
Questão 09
(Uem 2012) Joaquim coleciona artrópodes e, em sua coleção, encontra-se um animal com 20 patas, um animal com 18 patas, quatro animais com 8 patas e oito animais com 6 patas; todos com exatamente o número de patas mencionado e em perfeito estado. Considerando essas informações, assinale o que for correto.
01) A média do número de patas por animal é inferior a 8.
02) Os animais com 20 e 18 patas podem ser miriápodes.
04) Dentre os animais com 6 patas, podem ser encontrados percevejos, baratas e escorpiões.
08) A mediana do número de patas em cada indivíduo é 6.
16) Os animais de 8 patas podem possuir glândulas coxais em seu sistema excretor.
