Você sabia que o lançamento de peso é um lançamento horizontal? E cai nas provas do Enem. É a mesma matéria de "Lançamento Oblíquo de um Projétil", na Física. Aprenda agora.
Você sabia que o Brasil tem um recordista em lançamento de peso? Sim, Ronald Julião bateu recorde brasileiro de arremesso de peso indoor. Ele arremessou uma bola de chumbo, de 7,2 kg a uma marca de 17,94 m. Essa matéria cai no Enem: Lançamento Oblíquo de um Projétil.
O lançamento que Ronald Julião realizou, para bater o recorde, foi um lançamento horizontal, e é o mesmo tipo de lançamento que estudamos na Física. Agora você vai aprender os tipos, suas características e propriedades, que vão ajudar você, a se dar bem no Enem. Vem com a gente!

Lançamento oblíquo de um projétil
Quando lançamos uma bola, como a do lançamento de peso, ela não tem uma trajetória reta. Ela faz uma curva, subindo e descendo em seguida. Nesse lançamento, a velocidade de lançamento compõe com a horizontal, um ângulo de 0° e de 90°.
Complicou? Calma, que no vídeo o professor Diego Sousa, do canal do Curso Enem Gratuito, te explica tudo direitinho.
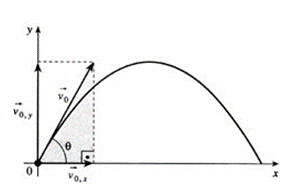
A velocidade V0 pode ser decomposta em duas componentes:
V0x = (Componente da velocidade eixo x) e
V0y = (Componente da velocidade eixo y):
V0x = V0 . Cos
V0y = V0 . Sen
O Lançamento Oblíquo é o resultado da junção de dois movimentos independentes:
– Movimento Horizontal – Esse Movimento é Uniforme, uma vez que V0x é constante (desprezando-se a resistência do ar).
– Movimento Vertical – Para esse movimento, a Velocidade é Variável, pois o corpo está sujeito à aceleração da gravidade: na subida, o Movimento é Retardado (A Velocidade e Aceleração têm sentidos contrários); na descida, o Movimento é Acelerado (A Velocidade e Aceleração têm o mesmo sentido).
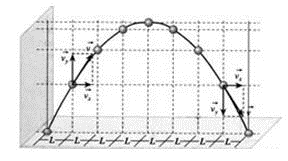
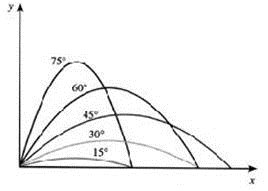
IMPORTANTE: O alcance é o mesmo para diferentes corpos lançados com a mesma velocidade inicial e com os ângulos de Lançamento Complementares (aqueles cuja soma vale 90°).
Velocidade e Aceleração no vértice da parábola formada pelo lançamento.
Quando mencionamos o ponto mais alto da trajetória, podemos dizer que, a componente vertical da velocidade do projétil, automaticamente irá se anular, e a velocidade irá diminuir à componente horizontal.
Observe a função a seguir:
V0x = V0 . Cosα
V0x = Velocidade inicial do eixo X, V0 = Velocidade inicial de Lançamento, Cox α = Cosseno do Ângulo Alfa
Propriedades Relativas ao ponto mais alto da Trajetória de Lançamento
Existem algumas propriedades que estão relacionadas com o pico mais alto da trajetória.
Observe:
1 – Sua Componente Vertical é nula, ou seja, Vy = 0.
2 – Sua Velocidade tem direção horizontal e apresenta um módulo igual à V0 . cosα.
3 – O módulo da Velocidade apresenta um valor muito pequeno.
4 – A Aceleração é composta por apenas uma componente chamada de Centrípeta, ou seja, a Aceleração Vetorial é perpendicular (forma ângulo de 90º) a velocidade vetorial.
5 – Um módulo de sua Aceleração Tangencial é nulo.
6 – Se o módulo da Aceleração Escalar for o mesmo da Aceleração Tangencial, a Aceleração Escalar será nula, ou seja, igual à zero.
Cálculo do tempo de Subida e do tempo de Queda
Para o cálculo do tempo de subida, podemos utilizar somente o movimento vertical. Observe:
Vy = V0y + Yy . t (MUV)
Vy = V0 . Senα – g t
Já quando for calcular o ponto mais alto, devemos pensar que:
t = ts e
Vy= 0, ou seja:

Quando os efeitos do ar são desprezados, o Tempo de Subida e o Tempo da Queda são iguais.
Observe:
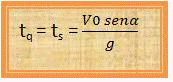
A Velocidade em um ponto qualquer do percurso
Utilizando um ponto qualquer de certa trajetória, das coordenadas (x; y), devemos saber que consequentemente sua velocidade terá duas componentes:
1 – A velocidade possui uma componente horizontal, que não depende do valor de x, que é a seguinte: Vx = V0 cosα.
2 – A velocidade possui também uma componente vertical Vy, representada por: Vy² = V²Oy + 2yy Δsy (Equação de Torricelli)
V² = V²0 (Senα)² – 2 g y
É muito importante lembrarmos que conseguimos a velocidade total pela junção vetorial entre Vx e Vy.
Observe:
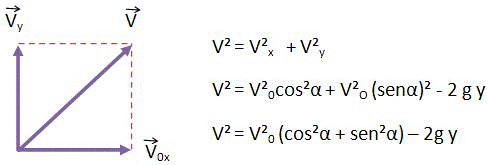
Cálculo da Altura Máxima
Com base nos princípios de Galileu, para o cálculo da altura máxima é necessário analisar o movimento vertical. Observe a função para o cálculo da altura máxima:

Cálculo do Alcance Horizontal
Com base nos princípios de Galileu, o alcance horizontal é calculado, a partir da análise do movimento horizontal. Observe a função para o cálculo do alcance horizontal:
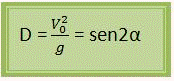
LEMBRETE IMPORTANTE:
* Quando V0 e g forem constantes, o alcance horizontal se tornará máximo, quando Sen2α = 1 (lembrando que esse é o valor máximo do seno). Observe:
![]()
Segue um pequeno vídeo para você fixar o assunto:
A seguir coloquei alguns exercícios para você treinar sobre o assunto. Eles já possuem as respostas, mas eu desafio você. Tente encontrar outras formas de resolver as questões, compare as duas, verifique as diferenças e post aqui no Blog. Tenho absoluta certeza de que você irá aprender muito mais assim. Um abração e nos encontramos aqui no Blog do Enem!
EXERCÍCIOS – Lançamento de Projétil
1. Um projétil é lançado com velocidade inicial de intensidade igual a 50 m/s. A trajetória faz na origem um ângulo de 37° com a horizontal. As intensidades da velocidade e da aceleração no ponto mais alto da trajetória são: Dados: sen 37° = 0,60; cos 37° = 0,80; g = 10 m/s2Despreza-se o efeito do ar.
a) v = 40 m/s; a = zero;
b) v = zero; a = zero;
c) v = 40 m/s; a = 10 m/s2;
d) v = 30 m/s; a = zero;
e) v = zero; a = 10 m/s2.
2. Em um local onde o efeito do ar é desprezível e g = 10 m/s2um nadador salta de um trampolim de 12m de altura e atinge a água a uma distância de 6,0 m, medida horizontalmente da borda do trampolim, em um intervalo de tempo de 2,0s. A velocidade do nadador no instante do salto tem intensidade igual a:
a) 3,0 m/s
b) 4,0 m/s
c) 1,0 m/s
d) 5,0 m/s
e) 7,0 m/s
3. (UECE) Num lugar em que g = 10 m/s2, lançamos um projétil com a velocidade de 100 m/s e formando com a horizontal um ângulo de elevação de 30°. A altura máxima será atingida após:
a) 3s
b) 4s
c) 5s
d) 10s
e) 15s
4. (FEI) Um projétil é lançado a partir do solo, com velocidade de intensidade v0 = 100 m/s. Quando retorna ao solo, sua distância ao ponto de lançamento (alcance) é de 1000 m. A menor velocidade do projétil durante seu movimento é aproximadamente:
a) zero
b) 100 m/s
c) 87 m/s
d) 70 m/s
e) 50 m/s
5. Ganhou destaque no voleibol brasileiro a jogada denominada “jornada nas estrelas”, na qual a bola arremessada de um lado da quadra sobe cerca de 20 m de altura antes de chegar ao adversário do outro lado. Quanto tempo, em segundos, a bola permanece no ar? Adote g = 10 m/s2e não considere o efeito do ar.
a) 20
b) 10
c) 5,0
d) 4,0
e) 2,0
6. No exato instante em que o revólver é acionado, no esquema da figura, a pessoa inicia uma queda livre vertical a partir do repouso. Desprezando-se resistência e empuxo do ar, considerando o campo de gravidade uniforme e desejando-se que o projétil atinja o coração da pessoa, escolha a posição conveniente para o cano do revólver:
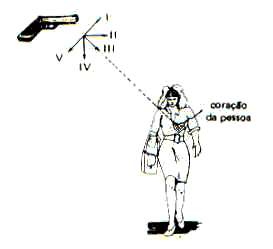
a) I
b) II
c) III
d) IV
e) V
GABARITO
| 01 – C | 02 – D | 03 – C | 04 – D | 05 – D |
| 06 – C |
Curso Enem Gratuito
Quer aumentar suas chances no próximo Exame Nacional do Ensino Médio e mandar bem nas Notas de Corte do Enem? Estude com as apostilas e aulas gratuitas do Curso Enem Online. Todas as matérias do Exame e ainda as Dicas de Redação. Acesse aqui o Curso Enem Gratuito Online.




