Entenda os fundamentos da Física dos Movimentos. São as fórmulas consagradas pelas teorias clássicas que abriram a cabeça da humanidade a partir das descobertas de Galileu Galilei, Johanes Kepler, Isaac Newton e outros 'pais da Física'.
Aprenda Física para o Enem e o Vestibular com o carro mais veloz do mundo. Entenda com ele os conceitos de Velocidade, Aceleração e Movimento! Tudo para você detonar no Enem! Chega mais!
Se você acha que o carro mais veloz do mundo é uma Ferrari ou uma Lamborghini, errou feio. É um Bugatti Veyron Super Sport! Sua velocidade máxima é 431 Km/h. Mais impressionante ainda: sua aceleração é de 0 a 100 km/h em 2,5 segundos. Estranhou? É, eu também acreditava que os modelos italianos eram os mais velozes, mas não são.  Mas você já parou pra pensar no que isto significa a marca absurda de 431 Km/h em um automóvel? Quer dizer que se fosse possível, colocar um carro, em sua velocidade máxima, de forma constante durante uma hora, este carro iria percorrer a incrível distância de 431 quilômetros.
Mas você já parou pra pensar no que isto significa a marca absurda de 431 Km/h em um automóvel? Quer dizer que se fosse possível, colocar um carro, em sua velocidade máxima, de forma constante durante uma hora, este carro iria percorrer a incrível distância de 431 quilômetros.
Seria como ir da cidade de São Paulo a cidade do Rio de Janeiro (PASME!) em apenas 1 hora! Mas, mesmo que você não saiba muito de física, você já sabe que manter um carro, no seu limite de velocidade de maneira constante, durante uma hora, não é possível.
Ainda mais com as nossas estradas brasileiras, não é? Hehehe. Mas, o mais importante aqui é aprendermos o que realmente significam os conceitos de velocidade e de aceleração.
Muitas pessoas confundem Velocidade e Aceleração, e acham que ambas significam a mesma coisa. Você sabe a diferença? Não? Então chega mais e aprenda tudo sobre velocidade, aceleração e movimento!
Velocidade:
Em Física, velocidade é a relação entre uma determinada distância percorrida e o tempo gasto para percorrer esta distância. Este trajeto é medido em metros e o tempo em segundo (m/s), no SI (Sistema Internacional de Unidades), também pode ser convertido para quilômetros para a distância, e horas para o tempo gasto.
A velocidade é uma grandeza vetorial representada por um vetor que possui direção, sentido e módulo. Velocímetro
Velocímetro
Para você entender melhor, existe uma fórmula para o cálculo da velocidade. 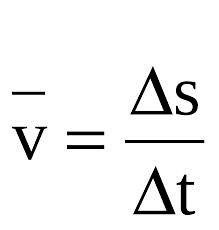
- Para você entender melhor, leia assim:
- Fórmula da Velocidade: ∆S = Variação de espaço ou distância
- ∆T = Variação do Tempo percorrido
- m/s = Metros dividido por Segundo
Dica do Blog: Bem como o que chamamos de macete, para transformar a Velô (velocidade para os não-íntimos) de Quilômetros por Hora (km/h) para Metros por Segundo (m/s) 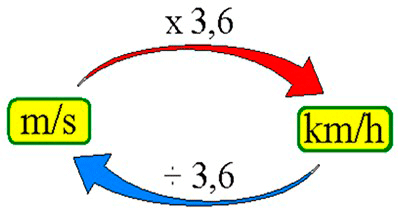 km/h = Quilômetros dividido por Hora.
km/h = Quilômetros dividido por Hora.
Existem alguns tipos de velocidade. É isso mesmo, Tipos de Velocidade. A velocidade que acabei de apresentar através da formula acima, é a mais comum, e é chamada de Velocidade Média.
Porém, existe um outro “tipo de velocidade” o qual vamos ver logo depois da aula-resumo sobre Movimento Retilíneo Uniforme. Veja a seguir:
Aula Gratuita – MRU
Confira com o professor Márcio Rosseto, do canal Curso Enem Gratuito, uma aula=show para você gabaritar nas questões da Física dos Movimentos no próximo Enem.
Velocidade Relativa:
Amigo(a), observe a imagem lá embaixo, você vai ver dois móveis A e B movendo-se em um mesmo percurso. Para esta situação, nós dizemos que suas velocidades são respectivamente vA e vB.
Em física, definimos velocidade escalar relativa de A em relação a B, como sendo a diferença entre as velocidade escalares do móvel A e do móvel B. Daí temos a expressão: vAB= vA– vB
Com isso, podemos concluir que tudo se passa como se o móvel B estivesse parado e o móvel A, em relação a ele, estivesse se movendo com uma velocidade escalar vAB.
Em muitos exercícios de cinemática, o sinal da velocidade relativa não é muito usado, ou seja, interessa o seu valor em módulo. LEMBRETE: O valor em MÓDULO, é sempre positivo.
Para o cálculo do valor em módulo da velocidade relativa, utilize duas regras práticas:
1° caso: se os dois móveis estiverem andando no mesmo sentido, o valor da velocidade relativa é dado pelo módulo da diferença entre os módulos das duas velocidades escalares. Observe como fica:
|vrel |= |vA |- |vB |
2° caso: se os dois móveis estiverem andando em sentidos contrários, o valor absoluto da velocidade relativa é dado pela soma dos módulos das duas velocidades escalares. Assim, temos:
|vrel |= |vA |+ |vB |
VA = Velocidade do móvel A VRel = Velocidade Relativa
VB = Velocidade do móvel B
É amigo(a), mas ainda resta outro problema: a Aceleração. Sim, pois muita gente acredita que a aceleração é a mesma coisa que velocidade. Mas não é! A aceleração depende da velocidade, ou seja, se não houver velocidade não existe aceleração. Além desta relação de dependência, os dois conceitos, envolvem outro assunto chamado MOVIMENTO.
Dica 1: Você sabe o que significa “Movimento”? Não? Então acesse o seguinte post do Blog do Enem https://blogdoenem.com.br/fisica-enem-cinematica/
Aceleração:
Ao observarmos um determinado automóvel, se deslocando percebemos que ele muda de velocidade com o passar do tempo. Quando a sua velocidade aumenta dizemos que o movimento é uniformemente acelerado.
Ou seja, ele se desloca de uma forma padrão, porém acelerada. O mesmo acontece quando ele diminui sua velocidade, dizemos então, que ele está em movimento uniformemente retardado, ou seja, ele também esta se deslocando de uma maneira padrão, porém de forma desacelerada.
Dica 2: Movimento uniformemente acelerado ou retardado, são conceitos importantíssimos dentro da Cinemática.
Parte da física que estuda os movimentos. Caso você tenha alguma dificuldade, em compreender este conteúdo, não hesite, vá até o Blog do Enem e relembre este e outros conceitos em https://blogdoenem.com.br/fisica-enem-cinematica/
MOVIMENTO UNIFORMEMENTE ACELERADO
T1 = Tempo gasto no primeiro instante V1 = Velocidade do primeiro momento
T2 = Tempo gasto no segundo instante V2 = Velocidade do segundo momento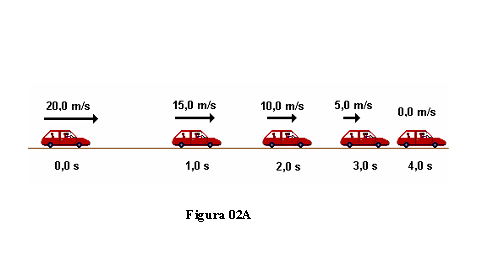
MOVIMENTO UNIFORMEMENTE RETARDADO
m/s = Metros dividido por Segundos
s = Segundos
Agora, para você fixar o assunto e finalizar sua revisão, veja esta excelente videoaula do canal Física Total.
A seguir coloquei alguns exercícios para você treinar sobre o assunto. Eles já possuem as respostas, mas eu desafio você. Tente encontrar outras formas de resolver as questões, compare as duas, verifique as diferenças e post aqui no Blog.
Tenho absoluta certeza de que você irá aprender muito mais assim. Um abração e nos encontramos aqui no Blog do Enem.
Aula Gratuita de MCU – Movimento Circular Uniforme.
Confira agora com o professor Márcio Rosseto uma aula-show sobre MCU – Movimento Circular Uniforme. Assista aqui mesmo o vídeo que está no canal Curso Enem Gratuito:
Questão 1
(PUC-MG) Uma mulher, caminhando na praia, deseja calcular sua velocidade. Para isso, ele conta o número de passadas que dá em um minuto, contando uma unidade a cada vez que o pé direito toca o solo, e conclui que são 50 passadas por minuto. A seguir, ele mede a distância entre duas posições sucessivas do seu pé direito e encontra o equivalente a seis pés. Sabendo que três pés correspondem a um metro, sua velocidade, suposta constante, é:

a) 3 km/h b) 4,5 km/h c) 6 km/h d) 9 km/h e) 10 km/h
Questão 2
(UDESC-SC) Dois caminhões deslocam-se com velocidade uniforme, em sentidos contrários, numa rodovia de mão dupla.

A velocidade do primeiro caminhão e a do segundo, em relação à rodovia, são iguais a 40 km/h e 50 km/h, respectivamente. Um caroneiro, no primeiro caminhão, verificou que o segundo caminhão levou apenas 1,0 s para passar por ele. O comprimento do segundo caminhão e a velocidade dele em relação ao caroneiro mencionado são, respectivamente, iguais a:
a) 25m e 90 km/h
b) 2,8m e 10 km/h
c) 4,0m e 25 m/s
d) 28m e 10 m/s
e) 14m e 50 km/h
RESOLUÇÃO:
01- Cada passada (duas posições sucessivas de seu pé direito) corresponde a 6 pés — como 3 pés correspondem a 1m,

6 pés corresponderão a 2m e, assim, cada passa corresponde a 2m —
Se ele efetua 50 passadas por minuto (60s), nesse intervalo de tempo ele percorre —
∆S = 50 . 2 = 100m —
V= ∆S/∆t = 100m / 60s / 3,6 = 100 . 3,6 / 60 = 360 / 60 = 6km/h
R- C.
02- Como os caminhões deslocam-se em sentidos opostos, o módulo da velocidade relativa entre eles é a soma de suas velocidades — VR = 50 + 40 = 90 km/h = 25 m/s — funciona como se o caroneiro estivesse parado e o segundo caminhão passando por ele com velocidade de VR = 25m/s, ou seja, essa é a velocidade com que o caroneiro vê o segundo caminhão passar por ele — comprimento L desse caminhão — VR = ΔS / Δt — 25 = L / 1 — L=25m —
R- A.
Os textos e imagens acima, foram elaborados, pelo Professor Wesley Oliveira, para o Blog do Enem. Wesley é formado em Física, pela Pontifícia Universidade Católica de São Paulo, e em Matemática pela UNISA – Universidade de Santo Amaro – São Paulo. Ministra aulas de Física e Matemática em escolas de São Paulo e da grande Florianópolis desde 2000. Facebook: https://www.facebook.com/profile.php?id=100011187033321




