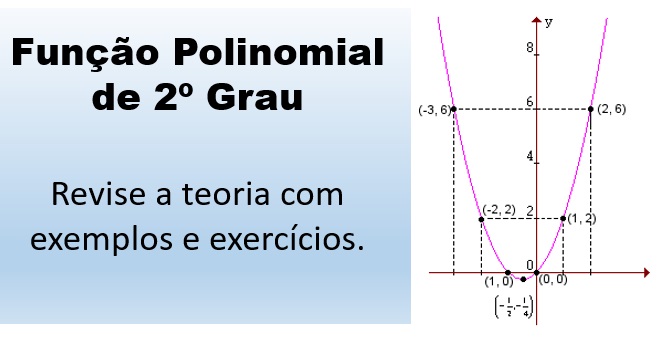
Revisão básica para você relembrar como resolver exercícios com a Função Polinomial de 2º Grau. É conteúdo frequente nas questões de Matemática dos vestibulares, do Enem, e do Encceja. Confira abaixo para garantir seus pontos.
Revisão sobre Função Polinomial do 2º Grau. Você lembra de tudo, ou quer lembrar um pouco mais? Veja abaixo. O começo do começo é sempre pela definição.
Depois vamos para as representações, operações, e exemplos do raciocínio para você compreender e, enfim, aprender e resolver sozinho os exercícios de Função Polinomial do 2º Grau. A representação gráfica dela é sempre uma parábola.
Temos que uma função polinomial do 2º grau é toda função escrita na forma: ![]() Complicou? Então, vamos simplificar… Veja no resumo a seguir uma explicação bem prática, pra você aprender de vez.
Complicou? Então, vamos simplificar… Veja no resumo a seguir uma explicação bem prática, pra você aprender de vez.
A Função Polinomial do 2º Grau
Confira com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito, o conceito e as explicações da Função Polinomial de 2º grau.
A base do cálculo algébrico é fundamental na resolução da maioria dos problemas envolvendo Matemática apresentados em vestibulares e no Enem. Venha revisar polinômios com o professor Sarkis na aula acima, e depois veja os exemplos abaixo! 😉
Exemplos de Função de 2º Grau:
a)![]() b)
b) ![]()
Raiz da Função
Se você já esqueceu, é hora de recordar: Raiz da Função é o valor de x que zera a função. Vamos utilizar as fórmulas clássicas para fixar bem a resolução: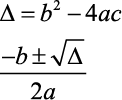
Ponto que intercepta o eixo y: Temos como valor que intercepta o eixo y (eixo das ordenadas) o coeficiente c.
Veja:
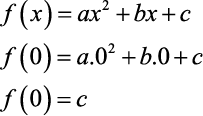
Portanto o ponto que intercepta o eixo das ordenadas é o ponto (0;c)
Vértice
Para você não esquecer: Vértice é o ponto que se encontra o valor máximo ou mínimo de uma função polinomial do 2º grau. E podemos encontrar o vértice utilizando as seguintes fórmulas: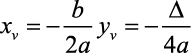
Gráfico
O gráfico de uma função polinomial do 2º grau será uma parábola, como você pode observar no exemplo abaixo: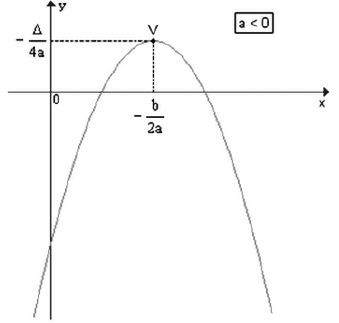
Analisando alguns gráficos podemos chegar a algumas conclusões gerais:
Parábola concavidade para baixo:
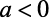
Parábola concavidade para cima:
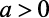
Valor mínimo para uma função 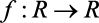
Para 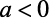 , não teremos valor mínimo, pois a função tende a menos infinito.
, não teremos valor mínimo, pois a função tende a menos infinito.
Para 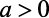 , o valor mínimo será o
, o valor mínimo será o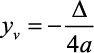
Para  , teremos valor mínimo, pois a função tende a menos infinito.
, teremos valor mínimo, pois a função tende a menos infinito.
Aprenda Funções de uma vez por todas
Aprenda agora com o professor Lucas Borguesan como resolver as questões de Funções nas provas do Enem, do Encceja, e dos vestibulares.
- A função é bem explorada nos vestibulares e no Enem.
- Ela é apresentada de diversas formas e inserida em diversos assuntos como Estatística, Matemática Financeira, e em várias situações problemas em outras áreas de conhecimento como Física, Biologia e Geografia.
- Nesta aula, o professor Lucas te ensina os conceitos de Funções e ainda te dá dicas de como resolver sem dificuldade os problemas matemáticos com funções.
Dica 2 – Revise sobre Função Polinomial do 1º grau, suas Classificações, Gráficos e como extrair a Raiz da Função em mais esta aula de Matemática Enem – https://blogdoenem.com.br/funcao-polinomial-matematica-enem/
Exercício Resolvido de Funções
(Uem 2012) O lucro de uma empresa em um período de 15 meses foi modelado matematicamente por meio da seguinte função f (x) = ax2 + bx + c, em que a variável x indica o mês e f (x) o lucro, em milhões de reais, obtido no mês x.
Sabe-se que no início desse período, digamos mês zero, a empresa tinha um lucro de 2 milhões de reais; no primeiro mês, o lucro foi de 3 milhões de reais; e, no décimo quinto mês, o lucro foi de 7 milhões de reais. Com base nessas informações, assinale o que for correto.
a) O lucro obtido no décimo quarto mês foi igual ao lucro obtido no oitavo mês.
b) O lucro máximo foi obtido no décimo mês.
c) O lucro máximo obtido foi superior a 7,5 milhões de reais.
d) O lucro da empresa nesse período de 15 meses oscilou de 2 a 7 milhões de reais.
e) O gráfico da função que modela o lucro é uma parábola com concavidade para baixo.
Gabarito: [a , c , e]
Dados Iniciais
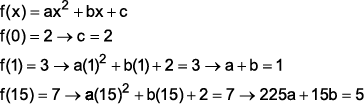
Resolvendo o sistema:
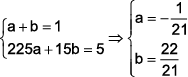
Portanto, a função é dada por
![]()
(a) Verdadeiro.
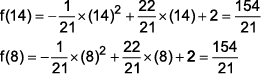
(b) Falso.
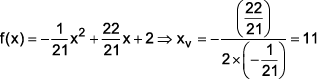
Portanto, décimo primeiro mês.
(c) Verdadeiro. O lucro máximo obtido é dado por:
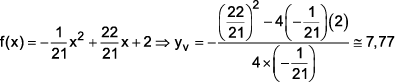
Portanto, superior a 7,5 milhões de reais.
(d) Falso. O lucro da empresa para x = 11 foi de 7,77 milhões de reais.
(e) Verdadeiro.
A função 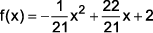 é uma parábola com concavidade para baixo, pois o coeficiente de x2 é negativo.
é uma parábola com concavidade para baixo, pois o coeficiente de x2 é negativo.
Desafios sobre as Funções Polinomiais
Questão 1
Um estudo das condições ambientais na região central de uma grande cidade indicou que a taxa média diária (C) de monóxido de carbono presente no ar é de 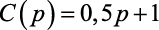 partes por milhão, para uma quantidade (p) milhares de habitantes.
partes por milhão, para uma quantidade (p) milhares de habitantes.
Estima-se que, daqui a t anos, a população nessa região será de 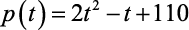 milhares de habitantes. Nesse contexto, para que a taxa média diária de monóxido de carbono ultrapasse o valor de 61 pares por milhão, é necessário que tenham sido transcorridos no mínimo:
milhares de habitantes. Nesse contexto, para que a taxa média diária de monóxido de carbono ultrapasse o valor de 61 pares por milhão, é necessário que tenham sido transcorridos no mínimo:
a) 2 anos
b) 2 anos e 6 meses
c) 3 anos
d) 3 anos e 6 meses
e) 4 anos
Dica 3 – Pronto para gabaritar na prova de matemática do Enem? Faça uma revisão com esta aula sobre Equações Polinomiais do 1º grau – https://blogdoenem.com.br/equacoes-polinomiais-1o-grau-matematica-enem/
Questão 2
O menor valor inteiro do parâmetro m, para que a função 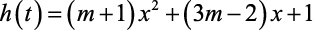 assuma valores positivos real, é:
assuma valores positivos real, é:
a) -1
b) 0
c) 1
d) 2
Questão 3
Sabendo que a expressão 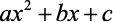 , onde a, b são números reais, é positiva, para qualquer x real, é correto afirma-se que:
, onde a, b são números reais, é positiva, para qualquer x real, é correto afirma-se que:
a) 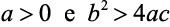
b) 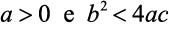
c) 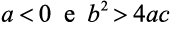
d) 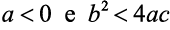
e) 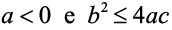
Questão 4
Se o gráfico da função quadrática
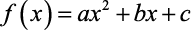
passa pelos pontos P(0;1), Q(-1;7) e R(2;7), então, o valor a+b-2c é igual a:
a) -2
b) -1
c) 2
d) 4
Questão 5
5. (Enem 2009) Um posto de combustível vende 10.000 litros de álcool por dia a R$ 1,50 cada litro. Seu proprietário percebeu que, para cada centavo de desconto que concedia por litro, eram vendidos 100 litros a mais por dia. Por exemplo, no dia em que o preço do álcool foi R$ 1,48, foram vendidos 10.200 litros.
Considerando x o valor, em centavos, do desconto dado no preço de cada litro, e V o valor, em R$, arrecadado por dia com a venda do álcool, então a expressão que relaciona V e x é
a) V = 10.000 + 50x – x2.
b) V = 10.000 + 50x + x2.
c) V = 15.000 – 50x – x2.
d) V = 15.000 + 50x – x2.
e) V = 15.000 – 50x + x2.
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!